 |

Financial
Management MGT201
VU
Lesson
11
SOME
SPECIAL AREAS OF CAPITAL
BUDGETING
Learning
Objectives:
In
this lecture, we will
discuss some special areas of
capital budgeting in which the
calculation
of
NPV & IRR is a bit more
difficult. These concepts
will be explained to you
with help of
numerical
example.
As
it is mentioned in the previous lectures
that we are studying the
area of capital budgeting
as
it
relates to projects, which means
investments in real assets (land,
property etc.) The major
difficulty in
the
NPV calculation is your
ability to forecast the cash
flows. Therefore, it is necessary
that one should
spent
time on this so that the
cash flow forecast is
accurate.
We,
have a simple formula to calculate the
cash flows. The way we
define the net
Incremental
after
tax cash flows for the
purposes of this course
is
Net
After-tax Cash Flows = Net
Operating Income + Depreciation +
Tax Savings from Depreciation
+
Net
Working Capital required for
this project + Other Cash
Flows
The
things we left out from the
formula given above are
certain incidental cash
flows (Include
Opportunity
Costs and Externalities but
Exclude Sunken Costs.)
Two
Major Criteria of Capital
Budgeting:
1.
Net Present Value
(NPV)
2.
Internal Rate of Return
(IRR)
a.
Combined View: NPV Profile
(NPV vs i Graph)
The
NPV is the most important
because it has a direct link
with shareholders wealth
maximization.
Let
us discuss in detail about the
difficulties faced in NPV & IRR
with the help of
certain
numerical
examples and explanations.
First,
we would discuss the case of
Multiple IRRs.
Multiple
IRR:
In
this case, you have a
project with certain cash
flows that are not
normal and when
you
try to calculate IRR you
obtain more than one IRR answer.
This is the case where you have
more
than
one sign change taking place
in your cash flow diagram.
Sign change means that
you have two
adjacent
arrows one of them is downward pointing & the
other one is upward pointing. In general,
our
cash
flow diagram starts with
down ward pointing arrow
(Investment) and it is followed
with series of
upward
pointing arrows (net incoming
cash) during the life of
project. However, during the
life of
project
if you have any net cash
outflow or downward pointing
arrow then that would be
second sign
change
and you can expect to have multiple
answer for IRR.
In
this particular case,
calculating the NPV and
setting it equal to zero to calculate
IRR will give
you
two answers & both of them
would be wrong.
The
alternative is to use Modified
IRR or MIRR approach.
MIRR
Approach:
The
logic behind MIRR is that
instead of looking at net cash flows
you look at cash inflows
and
outflows
separately for each point in
time. Discount all the
Outflows during the life to the
present and
Compound
all the Inflows to the termination date.
Assume reinvestment at a Cost of
Capital or Discount
Factor
(or Required Return) such as
the risk free interest rate.
The
MIRR represents the discount rate,
which will equate the Future
Value of cash inflows
to
Present
Value of cash
outflows.
Formula:
(1+MIRR)
n
=
CF
in *
(1+k) n-t
CF
out
/(1+k)
t
Modified
Internal Rate of Return
(MIRR) would provide us with
an answer, which is entirely
different
from
our previous IRR
calculations
Example:
A
project with the following
cash flows: Initial
Investment = -Rs100, Year 1 = +Rs500,
Year 2 = -
Rs500
If
we use standard NPV equation
to calculate the IRR
IRR
Equation: NPV = 0 = -100 +
500/ (1+IRR) - 500/ (1+IRR)
2
You
would come up with 2
answers
55

Financial
Management MGT201
VU
IRR
= 38% and 260%
Both
of these answers are
incorrect. Therefore, we will
use the modified IRR approach to
calculate the
actual
IRR for this
project.
MIRR
Approach (Assume Cost of Capital k =
10%):
(1+MIRR)
n
=
CF
in *
(1+k) n-t
CF
out
/
(1+k)
t
We
use 1.1 as compound factor
because we assume "i"=10% =
Risk free rate return.
Here`t' refers to
the
time in which a particular
cash flow occurs, while
`n' is the total life span
of the project.
(1+MIRR)
2
= 500
* (1+0.1)2-1
(100
/ 1.1) + (500 /
(1+0.1)2
(1+MIRR)
2
= 550
/ 513 = 1.07
MIRR
= 0.0344 = 3.44%
This
answer is entirely different
from the previous answers
that we got from calculating
the IRR.
However,
MIRR gives you the best
possible answer and the most realistic
too.
Now,
let us talk about the case
of comparing projects with different
lives.
NPV
of Projects with Different
Lives:
Suppose
that you have two projects
having different life spans.
It is not entirely accurate
to
calculate
NPV's in simple manner and
to compare them and pick the project
with higher NPV.
Because
you
are comparing a certain
project that is generating
cash flows for a short
period of time with
another
project
that is yielding cash flows
over a longer time. We use
following two approaches to
rank these
kinds
of projects.
1.
Common
Life Approach:
In
this approach, the idea is quite
simple. You need to bring
all the projects to the
same
length
in time. In other words, you
are required to convert all
the projects to the identical life
span.
You can do that by finding
least common multiple for common
life. For example, if
you
are
comparing two projects one
has life of 4 years and the
other, which has a life of 5
years, the
least
common multiple is 20 years. Sketch out
the cash flow diagram and
repeat the cash flow
for
each of the project such
that they fit in exact number of
time in 20 years. In case of
project
with
a life of 4 years, you can
replicate the cash flows 5 times in a
period of 20 years. . In
case
of
project with a life of 5
years, you can replicate the
cash flows 4 times in a period of 20
years.
Compute
the NPV of each project over
the common life and choose the
project with the highest
NPV.
2.
Equivalent
Annual ANNUITY (EAA)
Approach:
In
this case, our logic is to
find out that for a
particular project of limited
life giving you
the
certain net present value calculated in a
simple way, what kind of
yearly annuity gives the
same
NPV.
You can then compare annual
annuity of each project and
choose the highest. You are
comparing
cash
flow of two projects both of
which are taking place in a
period of one year only. You
can also
convert
the cash flows of the project to the
perpetuity, which is infinite,
and then you can compare
the
NPV's
like of different projects. That is
also correct since life
spans are identically
infinite.
Example:
We
have 2 Projects with following
Cash Flows:
Project
A: Io= - Rs100, Yr 1 =
+Rs200
Project
B: Io= - Rs200, Yr1= +Rs200,
Yr2= +Rs200
Simple
NPV Computation (assuming
i=10%):
NPV
Project A = -100 + 200/1.1 =
+Rs 82
NPV
Project B = -200 + 200/1.1 +
200/ (1.1)2
= +Rs
147
Conclusion
from Simple (or Normal)
NPV Calculation is that
Project B is better. It is incorrect
because
here
we are comparing apples to the
oranges since the project
lives are different!
Common
Life Approach:
Common
Life Span=Least common multiple = 2
Years (because this is the
shortest cycle in which
both
project
lives can exactly be
replicated back to back).
56
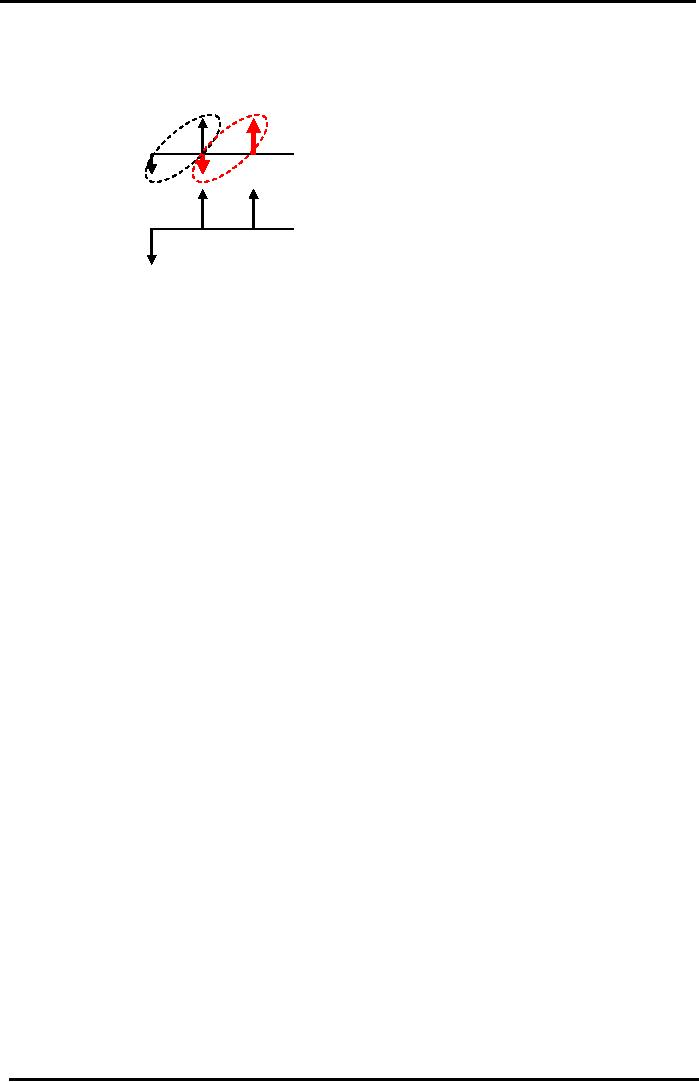
Financial
Management MGT201
VU
Project
A:
+200
+200
Yr
0
Yr
1
Yr
2
-100
-100
+200
+200
Project
B:
Yr
0
Yr
1
Yr
2
-200
In
this Cash Flow Pattern of A is
repeated exactly 2 times to cover the
life of the longer
Project
B.
The project A's outflow
100 & inflow of 200 then
we replicate it with down
ward pointing arrow
with
100 and upward pointing
arrow with 200 amount in the
2nd year. Project B remains
unchanged
Common
Life (C.L.)
NPV's:
Project
A C.L. NPV = -100 +
[(200-100)/1.1] + 200/
(1.1)2
= +Rs
156
Project
B C.L. NPV = Same as before
= +Rs 147
Now
our conclusion has changed!
After doing the Common Life
NPV, Project A looks better.
The
Simple
NPV of Project A was + Rs 82
but after increasing its
life to match Project B's,
the NPV of
Project
A increased. It is the correct answer. Also,
note that how the NPV of A
increased from 82 to
156
(almost
double) because you double
the life of the project.
Now
we solve this problem with
Equivalent Annual Annuity
Approach
Equivalent
Annual Annuity
Approach:
In
this we are explaining that
how we can achieve same NPV
value from an annuity
stream.
Here,
we are doing a back calculation
that we knew the NPV's but
which annuity stream they
are
representing
with in the life span of the
project. Then we compare the
annual annuity of both
projects.
The
life span remains
same
Example:
Start
with the Simple (or Normal)
NPV's calculated earlier (at i =
10%):
Project A Simple NPV = + Rs
82
Project B Simple NPV = + Rs
147
To
find EAA
Multiply
the Simple NPV of each
project by the EAA Factor
EAA
FACTOR = (1+
i) n
/
[(1+i) n
-1] where n =
life of project & i=discount
rate
Project
A's EAA Factor = 1.1 / (1.1-1) =
11
Project
B's EAA Factor = 1.12
/
(1.12-1) =
5.76
EAA
for each project
Project
A's EAA = Simple NPV * EAA Factor =
82*11= + Rs 902
Project
B's EAA = 147*5.76 = + Rs
847
Conclusion:
Project
A is better. Same conclusion as Common
Life Approach but of course
the
numbers
for EAA and NPV are
different.
Practical
view:
Companies
and individuals running different types
of businesses have to make the choice of the
asset
according
to the life span of the project.
For instance, a tailor shop
owner would have to decide
whether
to
invest in a sewing machine that
has a useful life of ten
years or to invest in another machine
with a
57

Financial
Management MGT201
VU
useful
life of three years. These decisions
are important since they
involve major cash outflows
of the
business.
There are advantages &
disadvantages associated with
different life span.
Different
Lives & Budget
Constraint:
Companies
and individuals running different types
of businesses have to make the choice of
the
asset
according to the life span of the
project.
Advantages
of asset with a long
life:
The
advantage of a longer asset life is
that the cash flows from the
project become more
predictable,
since there are lesser cash
outflows occurring during the
life of the project.
Disadvantage
of asset with very long
life:
It
does not give you the
opportunity (or option) to
extract full value of asset
and replace the
equipment
quickly in order to keep pace
with technology, better
quality, and lower
costs.
Advantages
of asset with short life
The
advantage of a short life asset is that
the investor, by making reinvestment in
the asset of a
superior
quality, lowers down the
costs and updates the project to the
new technological requirements.
Disadvantage
of assets with very short
life:
The
disadvantage is that the money will have
to be reinvested in some other project
with an
uncertain
NPV and return so it is risky. If a
good project is not
available, the money will
earn only a
minimal
return at the risk free interest
rate.
While
exercising the option of different
project timing, the projects can be
compared by applying
Common
Life and EAA Techniques to
quantitatively.
Budget
Constraint
We
have been addressing the issue of
capital budgeting with very
idealistic assumptions. In
practical
life, individuals and companies have a
limited amount of money and
limited human resources
in
terms of either skill or
numbers. It can be argued that the
firm can also meet
their requirements by
borrowing.
IN real life, managers may
avoid borrowing to limit
their risk exposure. This prevents
them
from
undertaking projects with high
positive NPVs that would
have added to the firm's value
and
maximized
shareholder wealth!
58
Table of Contents:
- INTRODUCTION TO FINANCIAL MANAGEMENT:Corporate Financing & Capital Structure,
- OBJECTIVES OF FINANCIAL MANAGEMENT, FINANCIAL ASSETS AND FINANCIAL MARKETS:Real Assets, Bond
- ANALYSIS OF FINANCIAL STATEMENTS:Basic Financial Statements, Profit & Loss account or Income Statement
- TIME VALUE OF MONEY:Discounting & Net Present Value (NPV), Interest Theory
- FINANCIAL FORECASTING AND FINANCIAL PLANNING:Planning Documents, Drawback of Percent of Sales Method
- PRESENT VALUE AND DISCOUNTING:Interest Rates for Discounting Calculations
- DISCOUNTING CASH FLOW ANALYSIS, ANNUITIES AND PERPETUITIES:Multiple Compounding
- CAPITAL BUDGETING AND CAPITAL BUDGETING TECHNIQUES:Techniques of capital budgeting, Pay back period
- NET PRESENT VALUE (NPV) AND INTERNAL RATE OF RETURN (IRR):RANKING TWO DIFFERENT INVESTMENTS
- PROJECT CASH FLOWS, PROJECT TIMING, COMPARING PROJECTS, AND MODIFIED INTERNAL RATE OF RETURN (MIRR)
- SOME SPECIAL AREAS OF CAPITAL BUDGETING:SOME SPECIAL AREAS OF CAPITAL BUDGETING, SOME SPECIAL AREAS OF CAPITAL BUDGETING
- CAPITAL RATIONING AND INTERPRETATION OF IRR AND NPV WITH LIMITED CAPITAL.:Types of Problems in Capital Rationing
- BONDS AND CLASSIFICATION OF BONDS:Textile Weaving Factory Case Study, Characteristics of bonds, Convertible Bonds
- BONDS’ VALUATION:Long Bond - Risk Theory, Bond Portfolio Theory, Interest Rate Tradeoff
- BONDS VALUATION AND YIELD ON BONDS:Present Value formula for the bond
- INTRODUCTION TO STOCKS AND STOCK VALUATION:Share Concept, Finite Investment
- COMMON STOCK PRICING AND DIVIDEND GROWTH MODELS:Preferred Stock, Perpetual Investment
- COMMON STOCKS – RATE OF RETURN AND EPS PRICING MODEL:Earnings per Share (EPS) Pricing Model
- INTRODUCTION TO RISK, RISK AND RETURN FOR A SINGLE STOCK INVESTMENT:Diversifiable Risk, Diversification
- RISK FOR A SINGLE STOCK INVESTMENT, PROBABILITY GRAPHS AND COEFFICIENT OF VARIATION
- 2- STOCK PORTFOLIO THEORY, RISK AND EXPECTED RETURN:Diversification, Definition of Terms
- PORTFOLIO RISK ANALYSIS AND EFFICIENT PORTFOLIO MAPS
- EFFICIENT PORTFOLIOS, MARKET RISK AND CAPITAL MARKET LINE (CML):Market Risk & Portfolio Theory
- STOCK BETA, PORTFOLIO BETA AND INTRODUCTION TO SECURITY MARKET LINE:MARKET, Calculating Portfolio Beta
- STOCK BETAS &RISK, SML& RETURN AND STOCK PRICES IN EFFICIENT MARKS:Interpretation of Result
- SML GRAPH AND CAPITAL ASSET PRICING MODEL:NPV Calculations & Capital Budgeting
- RISK AND PORTFOLIO THEORY, CAPM, CRITICISM OF CAPM AND APPLICATION OF RISK THEORY:Think Out of the Box
- INTRODUCTION TO DEBT, EFFICIENT MARKETS AND COST OF CAPITAL:Real Assets Markets, Debt vs. Equity
- WEIGHTED AVERAGE COST OF CAPITAL (WACC):Summary of Formulas
- BUSINESS RISK FACED BY FIRM, OPERATING LEVERAGE, BREAK EVEN POINT& RETURN ON EQUITY
- OPERATING LEVERAGE, FINANCIAL LEVERAGE, ROE, BREAK EVEN POINT AND BUSINESS RISK
- FINANCIAL LEVERAGE AND CAPITAL STRUCTURE:Capital Structure Theory
- MODIFICATIONS IN MILLAR MODIGLIANI CAPITAL STRUCTURE THEORY:Modified MM - With Bankruptcy Cost
- APPLICATION OF MILLER MODIGLIANI AND OTHER CAPITAL STRUCTURE THEORIES:Problem of the theory
- NET INCOME AND TAX SHIELD APPROACHES TO WACC:Traditionalists -Real Markets Example
- MANAGEMENT OF CAPITAL STRUCTURE:Practical Capital Structure Management
- DIVIDEND PAYOUT:Other Factors Affecting Dividend Policy, Residual Dividend Model
- APPLICATION OF RESIDUAL DIVIDEND MODEL:Dividend Payout Procedure, Dividend Schemes for Optimizing Share Price
- WORKING CAPITAL MANAGEMENT:Impact of working capital on Firm Value, Monthly Cash Budget
- CASH MANAGEMENT AND WORKING CAPITAL FINANCING:Inventory Management, Accounts Receivables Management:
- SHORT TERM FINANCING, LONG TERM FINANCING AND LEASE FINANCING:
- LEASE FINANCING AND TYPES OF LEASE FINANCING:Sale & Lease-Back, Lease Analyses & Calculations
- MERGERS AND ACQUISITIONS:Leveraged Buy-Outs (LBO’s), Mergers - Good or Bad?
- INTERNATIONAL FINANCE (MULTINATIONAL FINANCE):Major Issues Faced by Multinationals
- FINAL REVIEW OF ENTIRE COURSE ON FINANCIAL MANAGEMENT:Financial Statements and Ratios