 |

Financial
Management MGT201
VU
Lesson
27
RISK
AND PORTFOLIO THEORY, CAPM,
CRITICISM OF CAPM AND APPLICATION
OF
RISK
THEORY
Learning
Objectives:
After
going through this lecture,
you would be able to have an
understanding of the following
topics
·
Risk,
Portfolio Theory, CAPM
·
Criticisms
of CAPM
·
Applications
of Risk Theory
Today
we will review some concepts
about risk portfolio theory
and capital asset pricing
model.
There
is saying in English that
fortune favours the
brave.
Summary
of Single Stock (Stand
Alone) Risk &
Return:
The
first thing that we studied
was how to calculate the expected rate of
return or risk for a
single
stock that is what we call
stand alone investment.
Uncertainty comes along as we
are not what is
price
of the stock will be at any time in
future? Because of this
uncertainty there are possible
outcomes
of
such investment and we attach
probability or their likely
hood and we calculate a weighted
average in
order
to come up with expected rate of return
on the investment.
Expected
Return Formula (Weighted
Average of Many Possible
Future Outcomes for Returns
of that
one
Stock)
<r>=
∑
(p i
x
r
i)
(where p = probability of future outcome
and r is the rate
of
return from that
outcome
So,
if there are three possible outcomes
attached with it the formula
will be
<r>=PArA+PBrB+PCrC
Where,
p=possible outcomes. There is a
probablity distribution of such
outcomes and this
distribution
is the measure of the spread or range of possible
values or uncertainty. if we a look at
the
graph
of the normal distribution curve
then the width of the curve is the
measure of the risk or
uncertainty.
We measure risk mostly by
standard deviation.
Stand
Alone Total Risk Formula
(Standard Deviation or Spread of
Distribution of Possible
Future
Returns)
Sigma
= σ
=
(
∑
( r
i
- < r
i
>
)2
p
i
))
0.
5 =
(Var) 0.
5
This
formula which represents the
total risk of a single stock
can be used for the
portfolio of
stocks.
Portfolio
Risk & Return:
We
then spoke about the
collection of many stocks.
Why do sensible people
invest in many
stocks
the logic is very simple
that do not put all
your eggs in one basket. The
experimental studies have
shown
that if some one has 40
different stocks or investments which
are not correlated to each
other
then
half of the risk can be
eliminated. What kind of
risk has been eliminated?
This is the company's
specific
risk that has been
eliminated because of company's random
events in the life of the
company.
So,
the diversification or investment in increasing number
of stocks reduces the overall or
total risk and
even
if you diversified in 7 uncorrelated
stocks it is possible to reduce the large
portion of the
company's
own risk .once you have
known the return of the individual stock
you have known about
the
portfolio
stock in collection of investments. Expected rate of
return for 3 stocks on a
portfolio is:
Expected
Portfolio Return Formula
(Weighted Average of Returns of
Stocks in the Portfolio)
rP * =
rA xA
+ rB xB
+ rCxC
+ (for a
3-Stock Portfolio)
Portfolio
Risk Formula
σp
=
XA 2σ
+
XB2 σ
+
2 (XA XB
σ
Aσ
ρ
2
2
)
(2
Stocks)
B
AB
If
2 stocks move in the same
direction together then correlation
coefficient is 1.0. if the
exactly
move
in the opposite direction then the
correlation coefficient -1.0 and if there
is no relation between the
movement
of the stocks then the correlation
coefficient is zero.
If
More than 2 Stocks, then use
RISK MATRIX
116
Financial
Management MGT201
VU
3-Stock
Portfolio Risk
Formula
3
x 3 Matrix Approach
Stock
A
Stock
B
Stock
C
XA2
2
Stock
XA
XB
XA
XC
A
A
B
AB
A
C
AC
A
XB2
2
Stock
XB
XA
XB
XC
B
A
BA
B
B
C
BC
B
XC2
2
Stock
XC
XA
XC
XB
C
A
CA
C
B
CB
C
C
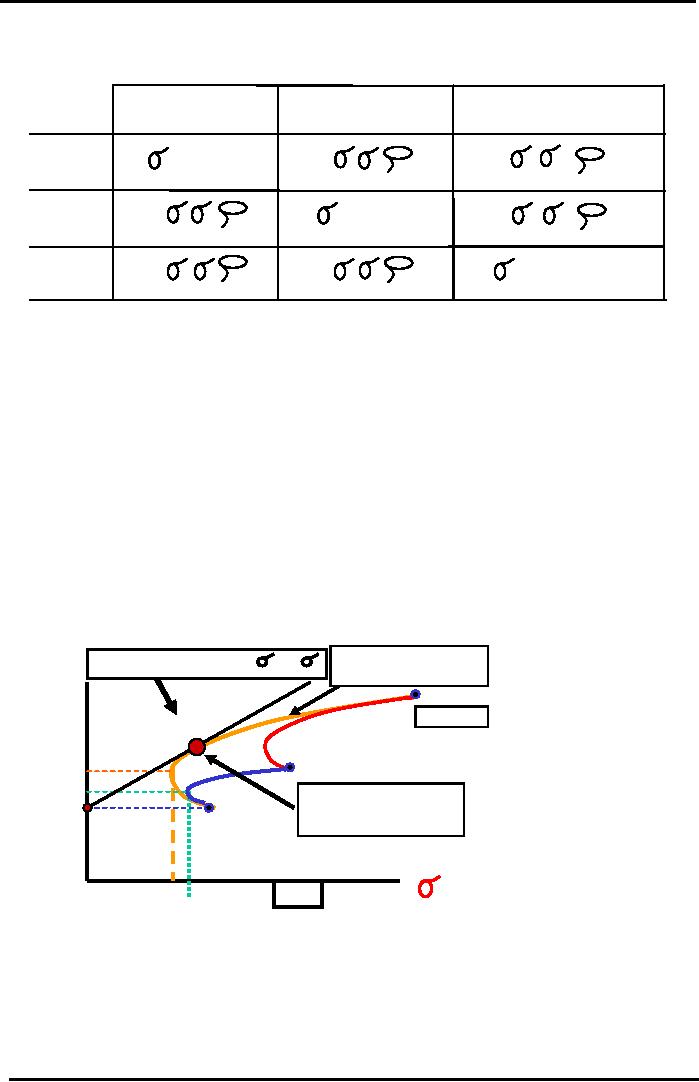
The
portfolio theory told us there is
direct relationship between risk and the
return and as risk of the
investment
goes up then return also
increase .it is mentioned
that if correlation co-efficient is
less then
or
equal to zero (ve) then
the risk and return relationship between
2 stocks exhibits shaped
curve what
it
tells us is that it is possible that
when we added the 3rd stock then it not only
increase the overall
return
but
it also reduce the total
risk of the portfolio and
that is ideal . We found the
parachute curve for
the
portfolio
which consist of more then 2
stocks and this large
hook is the efficient frontier
which
represents
the most efficient combination of the
different stocks in that
portfolio. By adding stock C we
came
up with parachute curve and
we also came up with curve
that envelops both of these
curves which
is
known as the efficient frontier.
So, let's see how
can we derive CML or the capital
market line and
the
equation of CML from this
efficient market curve
.portfolio return is with y-
axis and risk
along
with
x-axis we see the line from
risk free rate of return
which is assumed to be 10% and is
represented
by
rRF .
Picking
the Most Efficient
Portfolio
Capital
Market Line (CML) & T-Bill
Portfolio
P
Efficient
Frontier
rP* =
rRF + [ (rM
- rRF)
/
M]
rP*
for
3-Stock Portfolio
Portfo
30%
Capital
Market Line
Stock
C
lio
"The
Parachute"
Retur
Stock
A
20%
n
Optimal
Portfolio Mix
(50%A,
30% B, 20%C) if
10%=
Stock
B
rRF
Risk
Free T-Bill ROR =
10%
40%
20%
2.5%
P
Portfolio
with Negative
Risk
3.4%
or
Zero Correlation
Coefficient
Parachute
Graph and
Efficient Frontier (Hook
Shaped Curve) shows ALL possible
Risk-Return
Combinations
for ALL combinations of stocks in the
Portfolio whether efficient or
not.
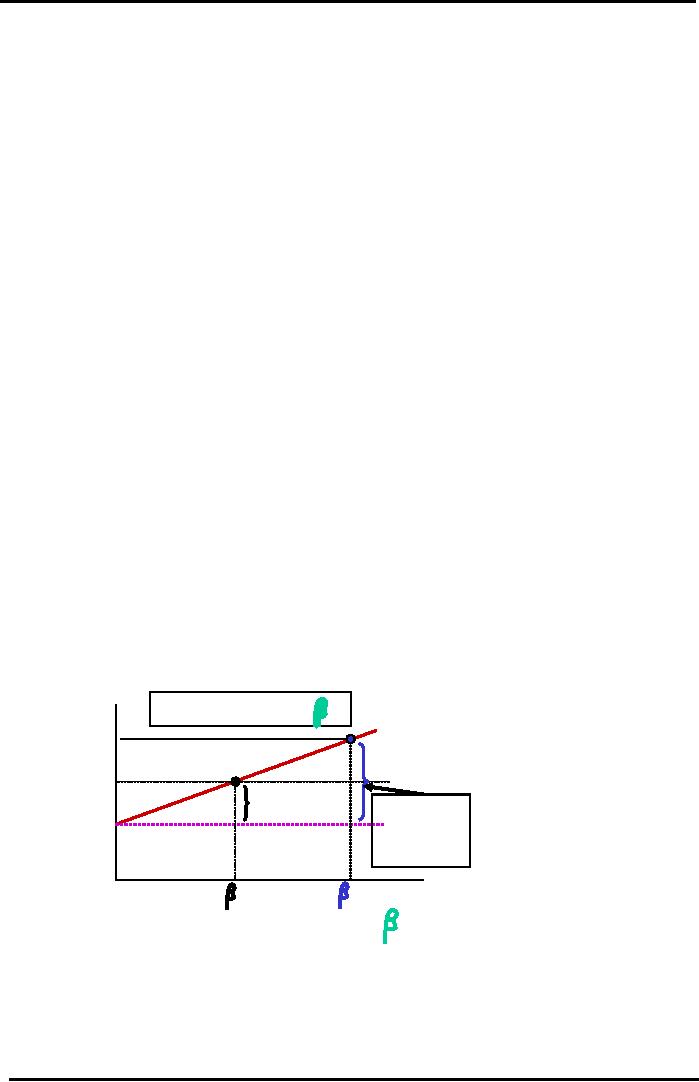
CML
Straight Line Equation (T-Bill
Portfolio and Optimal Portfolio Mix on
Efficient Frontier
Curve)
connects
rRF (Risk-free or T-Bill
return) to the Tangent Point on the
Efficient Frontier
Curve.
117
Financial
Management MGT201
VU
It
represents all Risk-Return
Combinations for Efficient
Portfolios
in the
Capital Market. We
assume
easy access to risk-free
T-Bill Portfolio. Portfolio
Risk measured using Standard
Deviation.
There
is an optimal point of the line
where
Stock
A=50%
Stock
B=30%
Stock
C=20%
Summary
of Beta:
Market
Risk and Beta Coefficient
(CAPM)
Single
Stock Beta (=Slope of Best
Fit Regression Line which
passes through data
points)
=
Percent Change in Stock ROR /
Percent Change in Market
Index ROR
Portfolio
Beta Risk Formula (Weighted
Average Formula)
Stock
Beta Formula in terms of Stock Standard
Deviation & Covariance
=
σ
A
σ
M
ρ
AM
/ σ 2
M
=
σ
A
ρ
AM
/ σ M
= market
risk
Security
Market Line (SML)
SML
(Security Market Line) -
Cornerstone of CAPM:
It
represents all Risk-Return
Combinations for ALL
Efficient Stocks in the
Capital Market. Stock
risk
measured using Beta. Market Price of a
Stock is determined by Required
Return on Stock which
depends
on Market Risk (not Total
Risk).You can not expect to receive
extra return (or
compensation)
for
taking on Company-Specific Risk
which Rational Investors have
eliminated! Efficient
Market
Prices
are based on Market Risk
Only and NOT Total
Risk.
The
Efficient Market will only
offer you a Return (and a
Share Price) which is the bare
minimum acceptable
to
rational diversified
Investors.
Required
ROR vs Expected
ROR
SML
Linear Equation & Graphical
Interpretation
Security
Market Line (SML)
ALL
Efficient Stocks in Efficient
Markets
Required
rA =
rRF +
(rM -
rRF )
Return
(r*)
A.
rA= 30%
Security
Marketrket
Risk
Line
rM=
20%
Ma
Premium
for
Risky
Stock A's
Avg
Stock = 10%
rRF= 10%
Total
Risk
Premium
=
30-10
= 20%
A
=+ 2.0
M
=+ 1.0
Beta
Risk (
)
Criticisms
of CAPM & Alternatives:
Weakness
in SML:
·
Not All Investors are
rich or well-informed enough to
hold Fully Diversified
Portfolios
therefore
Market Risk (and Betas) is
NOT the only relevant factor
in estimating Required
Return
and Stock Prices. Other
Efficient Market
Assumptions.
118
Financial
Management MGT201
VU
·
Taxes
and Brokerage Costs that
affect Investor's analysis and estimation
of Returns have
been
ignored
Weakness
in CML:
Not
All Investors are influential enough to
be able to Borrow at the T-Bill
Rate. Generally the
Borrowing
Rate is higher than the
Lending Rate.
Fama
& French:
CAPM
ignores 2 important determinants of Higher
Required ROR (1) smaller firms and
(2)
Low
Market-to-Book Ratio.
Arbitrage
Pricing Model:
Accounts
for several factors that affect
risk i.e. Tax, inflation,
oil price,...
Financial
Management Applications of Risk-Return
Theory (CAPM):
·
Practical
Real Asset Investment Decisions and
Capital Budgeting
The most important
NPV
(and PV) Equations uses
REQUIRED ROR (and NOT
Expected
ROR)
·
Actual
Share Pricing and
Investment in Securities
Gordon's
Formula for
Share Pricing uses PV of
Dividends which uses
REQUIRED
ROR
Risk
& Return - Must Consider
both:
In
this course we have studied the
following concepts of financial
management.
·
First Part of this
Course - Valuation or Calculating
NPV and PV which are
measures of
Return.
We ignored Risk and origins
of Required ROR.
·
Second Part of this
Course Application of PV Concept to
Valuation or Pricing of Bonds
(Debt)
and Shares (Equity). Again we
ignored Risk and origins of
Required ROR.
·
Part 3 of the Course Introduced
Risk and how it determines the Required
Return used in
NPV
and Share Price Formulas.
·
In Perfect Markets, Value depends
on Required Return which
depends on Market Risk
(and
not
Total Risk).
·
BUT, in Real Markets which
are Imperfect and
Inefficient, Total Risk is
important. It can
be
calculated using the Sigma (Standard Deviation)
Formulas, probabilities, and Expected
Return.
·
Total Risk and Expected Return
must BOTH be considered in Comparing
Investments.
·
Market Risk and Required
Return are Related to one another
Common
Life Applications of Risk
and Return
Theory:
Concepts
of Risk & Return Theory have
Wide Practical Applications that
require a Creative
Mind.
Expected
Value or Expected ROR or Expected
Payoff
Total
Risk or Standard Deviation (based on
Spread or Range of Breadth of
Possible ROR
outcomes)
= Unique + Market
Risk
Systematic
(or Market or No diversifiable)
Risk (= Beta A x Sigma M). Individual
Risk relative
to
Market or Industry.
·
Think
Out of the Box:
Social
Cost-Benefit Analysis of Power
Plant:
Environmental
and Village Relocation Risk,
Uncertain Savings
Court
Case Payoff: Claims &
Penalties
Uncertain
likelihood of success and Opponent,
Uncertain Payoff
Likelihood
of War: Capability & Intent (Game
Theory)
Magnitude
of Capability vs Uncertainty of
Intent
119
Table of Contents:
- INTRODUCTION TO FINANCIAL MANAGEMENT:Corporate Financing & Capital Structure,
- OBJECTIVES OF FINANCIAL MANAGEMENT, FINANCIAL ASSETS AND FINANCIAL MARKETS:Real Assets, Bond
- ANALYSIS OF FINANCIAL STATEMENTS:Basic Financial Statements, Profit & Loss account or Income Statement
- TIME VALUE OF MONEY:Discounting & Net Present Value (NPV), Interest Theory
- FINANCIAL FORECASTING AND FINANCIAL PLANNING:Planning Documents, Drawback of Percent of Sales Method
- PRESENT VALUE AND DISCOUNTING:Interest Rates for Discounting Calculations
- DISCOUNTING CASH FLOW ANALYSIS, ANNUITIES AND PERPETUITIES:Multiple Compounding
- CAPITAL BUDGETING AND CAPITAL BUDGETING TECHNIQUES:Techniques of capital budgeting, Pay back period
- NET PRESENT VALUE (NPV) AND INTERNAL RATE OF RETURN (IRR):RANKING TWO DIFFERENT INVESTMENTS
- PROJECT CASH FLOWS, PROJECT TIMING, COMPARING PROJECTS, AND MODIFIED INTERNAL RATE OF RETURN (MIRR)
- SOME SPECIAL AREAS OF CAPITAL BUDGETING:SOME SPECIAL AREAS OF CAPITAL BUDGETING, SOME SPECIAL AREAS OF CAPITAL BUDGETING
- CAPITAL RATIONING AND INTERPRETATION OF IRR AND NPV WITH LIMITED CAPITAL.:Types of Problems in Capital Rationing
- BONDS AND CLASSIFICATION OF BONDS:Textile Weaving Factory Case Study, Characteristics of bonds, Convertible Bonds
- BONDS’ VALUATION:Long Bond - Risk Theory, Bond Portfolio Theory, Interest Rate Tradeoff
- BONDS VALUATION AND YIELD ON BONDS:Present Value formula for the bond
- INTRODUCTION TO STOCKS AND STOCK VALUATION:Share Concept, Finite Investment
- COMMON STOCK PRICING AND DIVIDEND GROWTH MODELS:Preferred Stock, Perpetual Investment
- COMMON STOCKS – RATE OF RETURN AND EPS PRICING MODEL:Earnings per Share (EPS) Pricing Model
- INTRODUCTION TO RISK, RISK AND RETURN FOR A SINGLE STOCK INVESTMENT:Diversifiable Risk, Diversification
- RISK FOR A SINGLE STOCK INVESTMENT, PROBABILITY GRAPHS AND COEFFICIENT OF VARIATION
- 2- STOCK PORTFOLIO THEORY, RISK AND EXPECTED RETURN:Diversification, Definition of Terms
- PORTFOLIO RISK ANALYSIS AND EFFICIENT PORTFOLIO MAPS
- EFFICIENT PORTFOLIOS, MARKET RISK AND CAPITAL MARKET LINE (CML):Market Risk & Portfolio Theory
- STOCK BETA, PORTFOLIO BETA AND INTRODUCTION TO SECURITY MARKET LINE:MARKET, Calculating Portfolio Beta
- STOCK BETAS &RISK, SML& RETURN AND STOCK PRICES IN EFFICIENT MARKS:Interpretation of Result
- SML GRAPH AND CAPITAL ASSET PRICING MODEL:NPV Calculations & Capital Budgeting
- RISK AND PORTFOLIO THEORY, CAPM, CRITICISM OF CAPM AND APPLICATION OF RISK THEORY:Think Out of the Box
- INTRODUCTION TO DEBT, EFFICIENT MARKETS AND COST OF CAPITAL:Real Assets Markets, Debt vs. Equity
- WEIGHTED AVERAGE COST OF CAPITAL (WACC):Summary of Formulas
- BUSINESS RISK FACED BY FIRM, OPERATING LEVERAGE, BREAK EVEN POINT& RETURN ON EQUITY
- OPERATING LEVERAGE, FINANCIAL LEVERAGE, ROE, BREAK EVEN POINT AND BUSINESS RISK
- FINANCIAL LEVERAGE AND CAPITAL STRUCTURE:Capital Structure Theory
- MODIFICATIONS IN MILLAR MODIGLIANI CAPITAL STRUCTURE THEORY:Modified MM - With Bankruptcy Cost
- APPLICATION OF MILLER MODIGLIANI AND OTHER CAPITAL STRUCTURE THEORIES:Problem of the theory
- NET INCOME AND TAX SHIELD APPROACHES TO WACC:Traditionalists -Real Markets Example
- MANAGEMENT OF CAPITAL STRUCTURE:Practical Capital Structure Management
- DIVIDEND PAYOUT:Other Factors Affecting Dividend Policy, Residual Dividend Model
- APPLICATION OF RESIDUAL DIVIDEND MODEL:Dividend Payout Procedure, Dividend Schemes for Optimizing Share Price
- WORKING CAPITAL MANAGEMENT:Impact of working capital on Firm Value, Monthly Cash Budget
- CASH MANAGEMENT AND WORKING CAPITAL FINANCING:Inventory Management, Accounts Receivables Management:
- SHORT TERM FINANCING, LONG TERM FINANCING AND LEASE FINANCING:
- LEASE FINANCING AND TYPES OF LEASE FINANCING:Sale & Lease-Back, Lease Analyses & Calculations
- MERGERS AND ACQUISITIONS:Leveraged Buy-Outs (LBO’s), Mergers - Good or Bad?
- INTERNATIONAL FINANCE (MULTINATIONAL FINANCE):Major Issues Faced by Multinationals
- FINAL REVIEW OF ENTIRE COURSE ON FINANCIAL MANAGEMENT:Financial Statements and Ratios