 |
Problem Solving |
| << Introduction |
| Genetic Algorithms >> |

Artificial
Intelligence (CS607)
Lecture
No. 4 -10
2 Problem
Solving
In chapter
one, we discussed a few
factors that demonstrate
intelligence.
Problem
solving was one of them when
we referred to it using the
examples of a
mouse
searching a maze and the
next number in the sequence
problem.
Historically
people viewed the phenomena
of intelligence as strongly related
to
problem
solving. They used to think
that the person who is
able to solve more
and more
problems is more intelligent
than others.
In order to
understand how exactly
problem solving contributes to
intelligence, we
need to
find out how intelligent
species solve
problems.
2.1
Classical Approach
The classical
approach to solving a problem is
pretty simple. Given a
problem at
hand
use hit and trial
method to
check for various solutions
to that problem.
This
hit and trial approach
usually works well for
trivial problems and is referred
to
as the
classical approach to problem
solving.
Consider
the maze searching problem.
The mouse travels though
one path and
finds
that the path leads to a
dead end, it then back
tracks somewhat and
goes
along
some other path and again
finds that there is no way to
proceed. It goes on
performing
such search, trying
different solutions to solve
the problem until a
sequence of
turns in the maze takes it
to the cheese. Hence, of all
the solutions
the
mouse tries, the one that
reached the cheese was
the one that solved
the
problem.
Consider
that a toddler is to switch on
the light in a dark room. He
sees the
switchboard
having a number of buttons on
it. He presses one, nothing
happens,
he presses
the second one, the
fan gets on, he goes on
trying different buttons
till
at last
the room gets lighted and
his problem gets
solved.
Consider
another situation when we
have to open a combinational
lock of a
briefcase. It is a
lock which probably most of
you would have seen
where we
have
different numbers and we
adjust the individual
dials/digits to obtain a
combination
that opens the lock.
However, if we don't know
the correct
combination of
digits that open the
lock, we usually try 0-0-0,
7-7-7, 7-8-6 or any
such
combination for opening the
lock. We are solving this
problem in the same
manner as
the toddler did in the
light switch example.
All
this discussion has one
thing in common. That
different intelligent species
use
a similar
approach to solve the
problem at hand. This
approach is essentially
the
classical
way in which intelligent
species solve problems.
Technically we call
this
hit
and trial approach the
"Generate and Test"
approach.
2.2
Generate and Test
This is a
technical name given to the
classical way of solving
problems where we
generate
different combinations to solve
our problem, and the one
which solves
the
problem is taken as the
correct solution. The rest
of the combinations that
we
try
are considered as incorrect
solutions and hence are
destroyed.
15
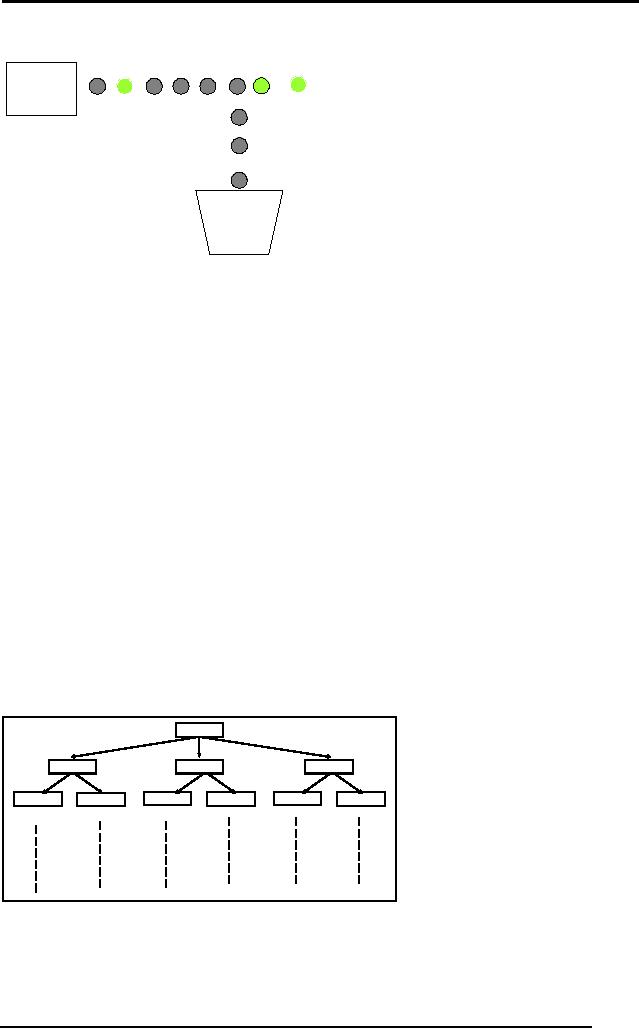
Artificial
Intelligence (CS607)
Possible
Tester
Correct
Solutions
Solutions
Solution
Generator
Incorrect
Solutions
The diagram
above shows a simple
arrangement of a Generate and
Test
procedure. The
box on the left labeled
"Solution
Generator" generates
different
solutions to a
problem at hand, e.g. in the
case of maze searching
problem, the
solution
generator can be thought of as a
machine that generates
different paths
inside a
maze. The "Tester" actually
checks that either a
possible solution
from
the
solution generates solves
out problem or not. Again in
case of maze
searching
the tester can be thought of
as a device that checks that
a path is a
valid
path for the mouse to
reach the cheese. In case
the tester verifies
the
solution to be a
valid path, the solution is
taken to be the "Correct
Solution".
On
the
other hand if the solution
was incorrect, it is discarded as
being an "Incorrect
Solution".
2.3 Problem
Representation
All
the problems that we have
seen till now were trivial
in nature. When the
magnitude of
the problem increases and
more parameters are added,
e.g. the
problem of
developing a time table,
then we have to come up with
procedures
better
than simple Generate and
Test approach.
Before
even thinking of developing
techniques to systematically solve
the
problem, we
need to know one more
thing that is true about
problem solving
namely
problem representation. The key to
problem solving is actually
good
representation of
a problem. Natural representation of
problems is usually
done
using
graphics and diagrams to develop a
clear picture of the problem
in your
mind. As an
example to our comment
consider the diagram
below.
OFF |
OFF | OFF
OFF
ON | OFF |
OFF
OFF | ON |
OFF
OFF |
OFF | ON
ON | ON |
OFF
ON | OFF |
ON
OFF | ON |
ON
OFF | ON |
ON
ON | ON |
OFF
ON | OFF |
ON
It shows
the problem of switching on
the light by a toddler in a
graphical form.
Each
rectangle represents the
state of the switch board.
OFF | OFF| OFF
means
that
all the three switches
are OFF. Similarly OFF| ON |
OFF means that the
first
and the
last switch is OFF and
the middle one is ON.
Starting from the
state
when
all the switches are
OFF the child can
proceed in any of the three
ways by
16

Artificial
Intelligence (CS607)
switching
either one of the switch ON.
This brings the toddler to
the next level in
the
tree. Now from here he can
explore the other options,
till he gets to a
state
where
the switch corresponding to
the light is ON. Hence
our problem was
reduced to
finding a node in the tree
which ON is the place
corresponding to the
light
switch. Observe how
representing a problem in a nice
manner clarifies the
approach to be
taken in order to solve
it.
2.4 Components of
Problem Solving
Let us
now be a bit more formal in
dealing with problem solving
and take a look at
the
topic with reference to some
components that constitute
problem solving.
They
are namely: Problem
Statement, Goal State,
Solution Space and
Operators.
We will
discuss each one of them in
detail.
2.4.1 Problem
Statement
This is
the very essential component
where by we get to know what
exactly the
problem at
hand is. The two major
things that we get to know
about the problem
is the
Information about what is to be
done and constraints to
which our solution
should
comply. For example we might
just say that given
infinite amount of
time,
one will be
able to solve any problem he
wishes to solve. But the
constraint
"infinite amount of
time" is
not a practical one. Hence
whenever addressing a
problem we
have to see that how
much time shall out
solution take at max.
Time
is not
the only constraint.
Availability of resources, and
all the other
parameters
laid
down in the problem
statement actually tells us
about all the rules
that have
to be followed
while solving a problem. For
example, taking the same
example of
the
mouse, are problem statement
will tell us things like,
the mouse has to
reach
the
cheese as soon as possible and in
case it is unable to find a
path within an
hour, it
might die of hunger. The
statement might as well tell
us that the mouse is
located in
the lower left corner of
the maze and the cheese in
the top left
corner,
the
mouse can turn left,
right and might or might
not be allowed to
move
backward and
things like that. Thus it is
the problem statement that
gives us a
feel of
what exactly to do and helps
us start thinking of how exactly
things will
work in
the solution.
2.4.2 Problem
Solution
While
solving a problem, this
should be known that what
will be out ultimate
aim.
That is
what should be the output of
our procedure in order to
solve the problem.
For
example in the case of
mouse, the ultimate aim is
to reach the cheese.
The
state of
world when mouse will be
beside the cheese and
probably eating it
defines
the aim. This state of
world is also referred to as
the Goal State
or
the
state
that represents the solution
of the problem.
2.4.3 Solution
space
In order to
reach the solution we need
to check various strategies. We
might or
might
not follow a systematic
strategy in all the cases.
Whatever we follow, we
have to go
though a certain amount of
states of nature to reach
the solution. For
example
when the mouse was in
the lower left corner of
the maze, represents
a
state
i.e. the start state.
When it was stuck in some
corner of the maze
represents a
state. When it was stuck
somewhere else represents
another state.
When it
was traveling on a path
represents some other state
and finally when it
17
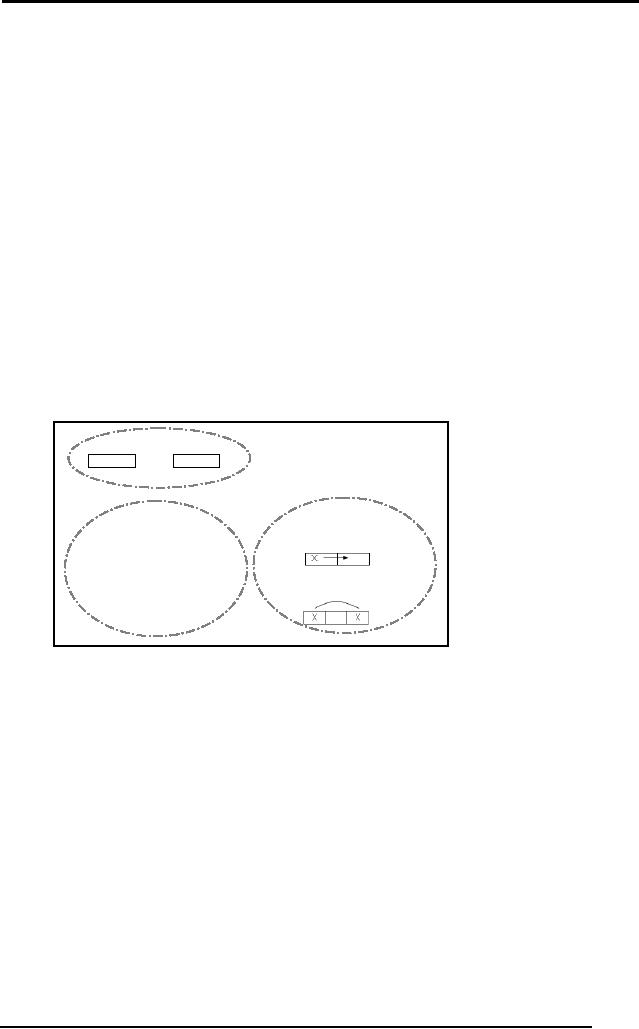
Artificial
Intelligence (CS607)
reaches
the cheese represents a
state called the goal
state. The set of the
start
state,
the goal state and
all the intermediate states
constitutes something
which
is called a
solution
space.
2.4.4 Traveling in
the solution space
We have to
travel inside this solution
space in order to find a
solution to our
problem. The
traveling inside a solution
space requires something
called as
"operators". In case of
the mouse example, turn left, turn right, go straight
are
the
operators which help us
travel inside the solution
space. In short the
action
that
takes us from one state to
the other is referred to as an
operator. So
while
solving a
problem we should clearly
know that what are
the operators that we
can
use in
order to reach the goal
state from the starting
state. The sequence
of
these
operators is actually
the solution to our
problem.
2.5
The Two-One Problem
In order to
explain the four components
of problem solving in a better
way we
have
chosen a simple but
interesting problem to help you
grasp the concepts.
The diagram
below shows the setting of
our problem called the
Two-One
Problem.
Start
Goal
11?22
22?11
Legal
Moves:
�
Slide
Rules:
� 1s'
move right
� 2s'
move left
�
Hop
� Only
one move at a time
� No backing
up
A simple
problem statement to the
problem at hand is as
under.
You are
given a rectangular container
that has 5 slots in it.
Each slot can
hold
only
one coin at a time. Place
Rs.1 coins in the two
left slots; keep the
center slot
empty and
put Rs.2 coins in the
two right slots. A simple
representation can be
seen in
the diagram above where
the top left container
represents the Start
State
in which
the coined are placed as
just described. Our aim is
to reach a state of
the
container where the left
two slots should contain
Rs.2 coins, the center
slot
should be
empty and the right two
slots should contain Rs.1
coin as shown in the
Goal
State. There
are certain simple rules to
play this game. The rules
are
mentioned
clearly in the diagram under
the heading of "Rules". The
rules actually
define
the constraints under which
the problem has to be
solved. The legal
moves
are the Operators
that
we can use to get from
one state to the other.
For
example we
can slide a coin to its
left or right if the left or
right slot is empty,
or
we can hop
the coin over a single
slot. The rules say that
Rs.1 coins can slide
or
hop only
towards right. Similarly the
Rs.2 coins can slide or hop
only towards the
left. You
can only move one coin at a
time.
18

Artificial
Intelligence (CS607)
Now let us
try to solve the problem in
a trivial manner just by
using a hit and
trial
method
without addressing the
problem in a systematic
manner.
Trial
1
Start
State
Move 1
Move 2
Move 3
Move 4
Move 5
In Move 1 we slide
a 2 to the left, then we hop a 1 to
the right, then we slide
the 2
to the
left again and then we hop
the 2 to the left, then
slide the one to the
right
hence at
least one 2 and one 1 are at the
desired positions as required in
the
goal
state but then we are
stuck. There is no other
valid move which takes us
out
of this
state. Let us consider
another trial.
Trial
2
19
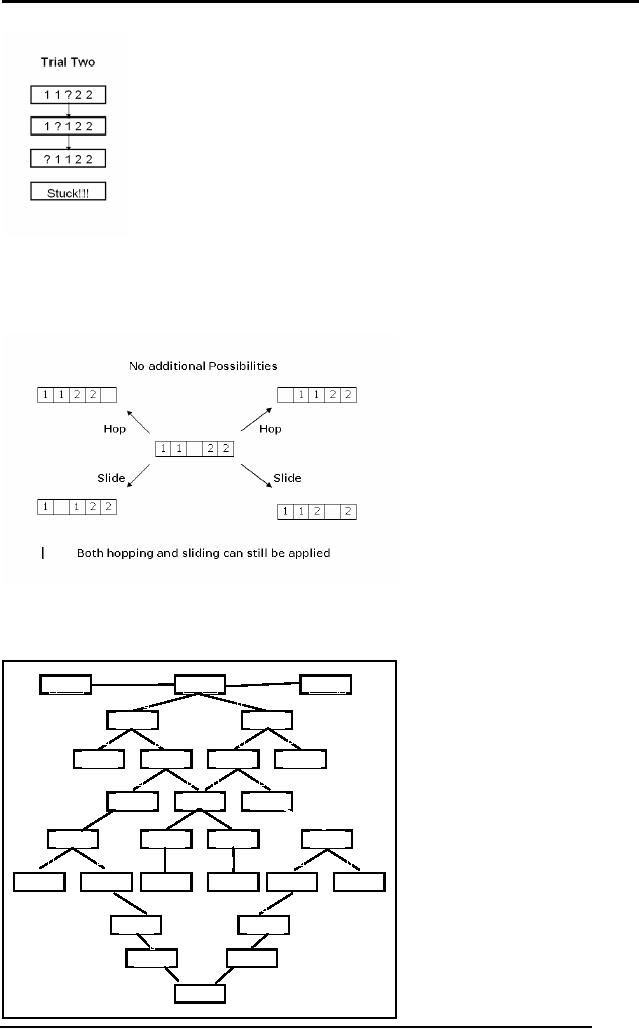
Artificial
Intelligence (CS607)
Starting
from the start state we
first hop a 1 to the right,
then we slide the other
1
to the
right and then suddenly we
get STUCK!! Hence
solving the problem
through a
hit and trial might not
give us the solution.
Let us now
try to address the problem
in a systematic manner. Consider
the
diagram
below.
Starting
from the goal state if we
hop, we get stuck. If we
slide we can further
carry
on. Keeping this observation
in mind let us now try to
develop all the
possible
combinations that can happen
after we slide.
H
H
?1122
11?22
1122
?
S
S
1?122
1 1 2? 2
S
S
H
H
?1122
1 2 1? 2
1?212
1122
?
S
S
S
S
1212
?
12
?12
?1212
H
H
H
H
12?21
?2112
1 2 2 1?
21?12
S
H
H
S
S
S
1 2 2? 1
?2121
2?112
1 2 2 ?1
2112
?
2?112
S
S
2?121
212
?1
H
H
2?211
2 2 1? 1
S
S
1 1? 2 2
20
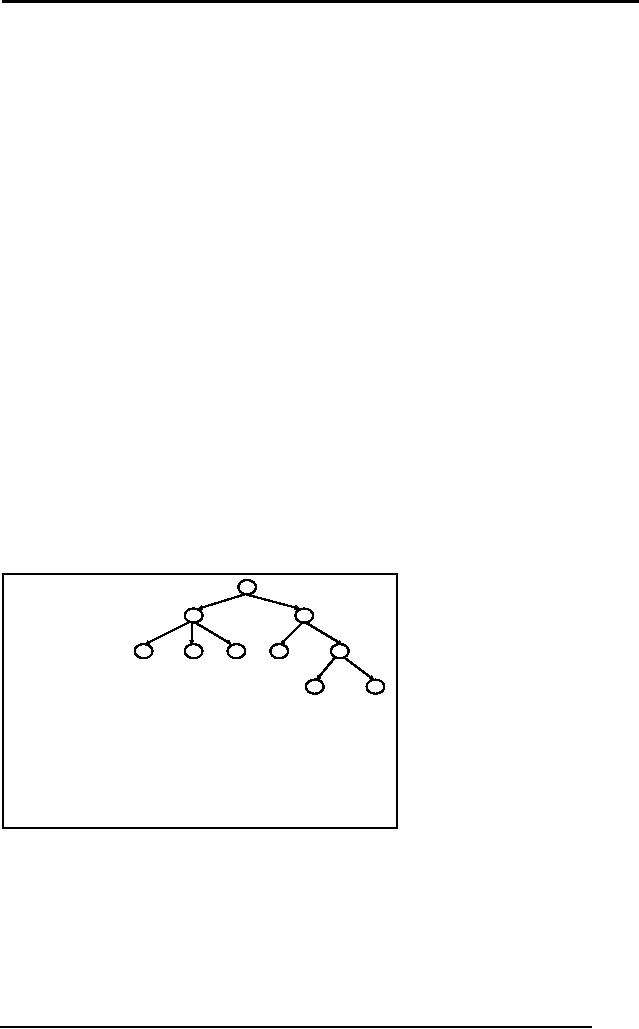
Artificial
Intelligence (CS607)
The diagram
above shows a tree sort of
structure enumerating all
the possible
states and
moves. Looking at this
diagram we can easily figure
out the solution to
our
problem. This tree like
structure actually represents
the "Solution
Space" of
this
problem. The labels on the
links are H and S
representing hop and
slide
operators
respectively. Hence H and S are
the operators that help us
travel
through
this solution space in order
to reach the goal state
from the start
state.
We hope
that this example actually
clarifies the terms problem
statement, start
state,
goal state, solution space
and operators in your mind. It
will be a nice
exercise to
design your own simple
problems and try to identify
these
components in
them in order to develop a
better understanding.
2.6
Searching
All
the problems that we have
looked at can be converted to a
form where we
have to
start from a start state
and search
for a
goal state by traveling
through a
solution
space. Searching is a formal
mechanism to explore
alternatives.
Most of
the solution spaces for
problems can be represented in a
graph where
nodes
represent different states and
edges represent the operator
which takes us
from
one state to the other. If
we can get our grips on
algorithms that deal
with
searching
techniques in graphs and trees,
we'll be all set to perform
problem
solving in an
efficient manner.
2.7
Tree and Graphs
Terminology
Before
studying the searching
techniques defined on trees and
graphs let us
briefly
review some underlying
terminology.
A
B
C
D
E
F
G
H
�"A" is
the "root node"
I
J
�"A, B, C .... J"
are "nodes"
�"B" is a
"child" of "A"
�"A" is
ancestor of "D"
�"D" is a
descendant of "A"
�"D, E, F, G, I,
J" are "leaf nodes"
�Arrows
represent "edges" or
"links"
The diagram
above is just to refresh
your memories on the
terminology of a tree.
As for
graphs, there are undirected
and directed graphs which
can be seen in the
diagram
below.
21
Artificial
Intelligence (CS607)
A
A
B
C
B
C
D
E
F
G
D
E
F
G
H
I
H
I
Directed
Graph
Undirected
Graph
Let us
first consider a couple of
examples to learn how graphs
can represent
important
information by the help of
nodes and edges.
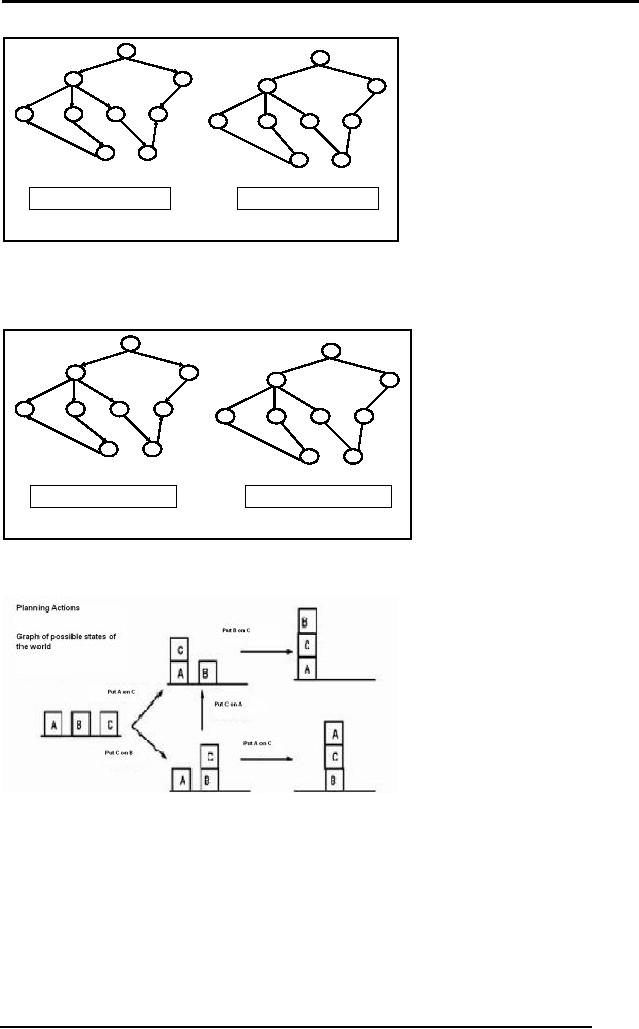
Graphs
can be used to represent
city routes.
A
A
B
C
B
C
D
E
F
G
D
E
F
G
H
I
H
I
Directed
Graph
Undirected
Graph
Graphs
can be used to plan
actions.
We will
use graphs to represent
problems and their solution
spaces. One thing to
be noted is
that every graph can be
converted into a tree, by
replicating the
nodes.
Consider the following
example.
22
Artificial
Intelligence (CS607)
S
3
3
A
A
D
B
C
B
D
A
E
G
S
S
C
E
E
B
B
F
3
2
D
F
B
F
C
E
A
C
G
F
E
D
1
3
F
G
C
G
G
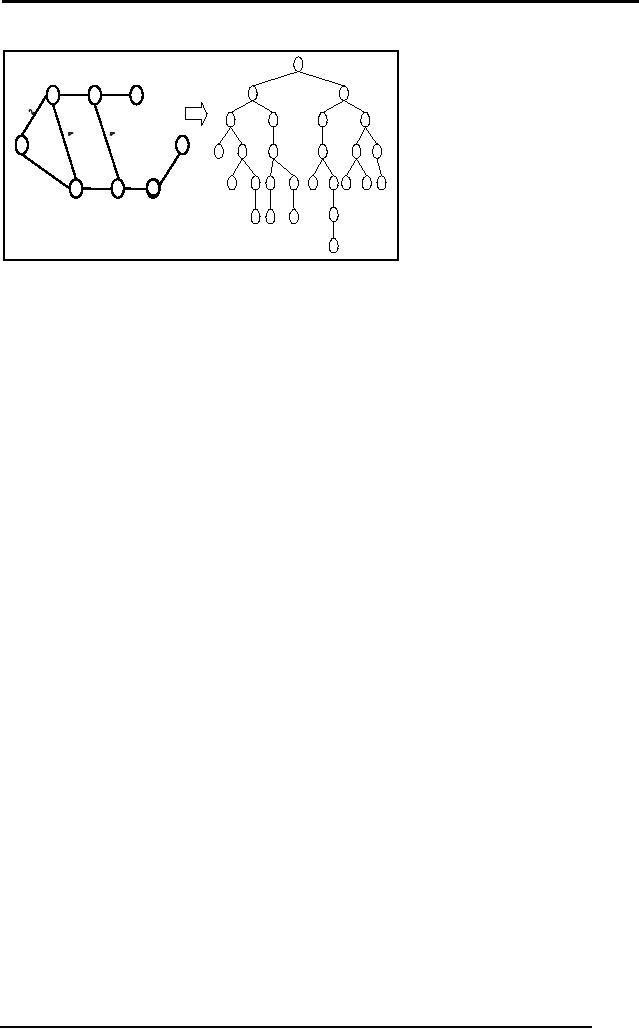
The graph in
the figure represents a city
map with cities labeled as
S, A, B, C, D,
E, F and G.
Just by following a simple
procedure we can convert
this graph to a
tree.
Start
from node S and make it the
root of your tree, check
how many nodes
are
adjacent to
it. In this case A and D are
adjacent to it. Hence in the
tree make A
and D, children of
S. Now go on proceeding in this manner
and you'll get a tree
with a
few nodes replicated. In
this manner depending on a
starting node you can
get a
different tree too. But
just recall that when
solving a problem; we
usually
know
the start state and
the end state. So we will be
able to transform our
problem
graphs in problem trees. Now if we
can develop understanding
of
algorithms
that are defined for
tree searching and tree
traversals then we will
be
in a better
shape to solve problems
efficiently.
We know
that problems can be
represented in graphs, and are
well familiar with
the
components of problem solving,
let us now address problem
solving in a
more
formal manner and study the
searching techniques in detail so
that we can
systematically
approach the solution to a
given problem.
2.8
Search Strategies
Search
strategies and algorithms
that we will study are
primarily of four
types,
blind/uninformed,
informed/heuristic, any path/non-optimal and
optimal path
search
algorithms. We will discuss
each of these using the
same mouse
example.
Suppose
the mouse does not
know where and how far is
the cheese and is
totally
blind to the configuration of
the maze. The mouse would
blindly search the
maze
without any hints that will
help it turning left or
right at any junction. The
mouse
will purely use a hit
and trial approach and will
check all combinations
till
one takes it to
the cheese. Such searching
is called blind or
uninformed
searching.
Consider
now that the cheese is
fresh and the smell of
cheese is spread
through
the
maze. The mouse will now
use this smell as a guide,
or heuristic (we will
comment on
this word in detail later)
to guess the position of the
cheese and
choose
the best from the
alternative choices. As the
smell gets stronger,
the
23

Artificial
Intelligence (CS607)
mouse
knows that the cheese is
closer. Hence the mouse is
informed about the
cheese
through the smell and
thus performs an informed
search in the maze.
For
now you might think that
the informed search will
always give us a
better
solution and
will always solve our
problem. This might not be
true as you will
find
out
when we discuss the word
heuristic in detail
later.
When
solving the maze search
problem, we saw that the
mouse can reach
the
cheese
from different paths. In the
diagram above two possible
paths are shown.
In any-path/non
optimal searches we are
concerned with finding any one
solution
to our
problem. As soon as we find a
solution, we stop, without
thinking that there
might as
well be a better way to
solve the problem which
might take lesser
time
or fewer
operators.
Contrary to
this, in optimal path
searches we try to find the
best solution. For
example, in
the diagram above the
optimal path is the blue one
because it is
smaller
and requires lesser
operators. Hence in optimal
searches we find
solutions
that are least costly,
where cost of the solution
may be different for
each
problem.
2.9 Simple
Search Algorithm
Let us
now state a simple search
algorithm that will try to
give you an idea
about
the
sort of data structures that
will be used while
searching, and the stop
criteria
for
your search. The strength of
the algorithm is such that
we will be able to
use
this
algorithm for both Depth
First Search (DFS) and
Breadth First Search
(BFS).
Let S be the start
state
1. Initialize Q
with the start node Q=(S) as the only entry; set
Visited =
(S)
2. If Q is empty,
fail. Else pick node X from Q
3. If X is a goal, return X,
we've reached the goal
4. (Otherwise)
Remove X from Q
5. Find all the children of
state X not in Visited
6. Add these to Q;
Add Children of X to Visited
7. Go to Step
2
Here Q
represents a priority queue. The
algorithm is simple and doesn't
need
much
explanation. We will use
this algorithm to implement
blind and uninformed
searches. The
algorithm however can be
used to implement informed
searches
24
Artificial
Intelligence (CS607)
as well. The
critical step in the Simple
Search Algorithm is picking of a
node X
from Q
according to a priority function.
Let us call this function
P(n). While using
this
algorithm for any of the
techniques, our priority
will be to reduce the value
of
P(n) as
much as we can. In other
words, the node with
the highest priority
will
have
the smallest value of the
function P(n) where n is the
node referred to as X
in the
algorithm.
2.10 Simple
Search Algorithm Applied to Depth First
Search
Depth
First Search dives into a
tree deeper and deeper to
fine the goal state.
We
will
use the same Simple
Search Algorithm to implement
DFS by keeping our
priority
function as
1
P(n) =
height
(n)
As mentioned
previously we will give
priority to the element with
minimum P(n)
hence
the node with the
largest value of height will
be at the maximum priority
to
be picked
from Q. The following sequence of
diagrams will show you how
DFS
works on a
tree using the Simple
Search Algorithm.
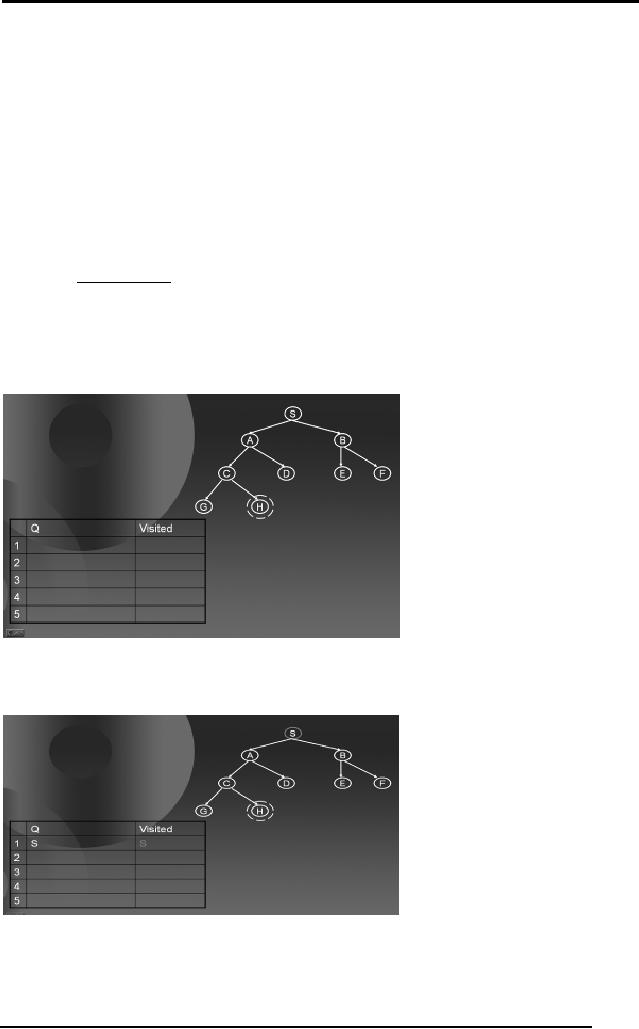
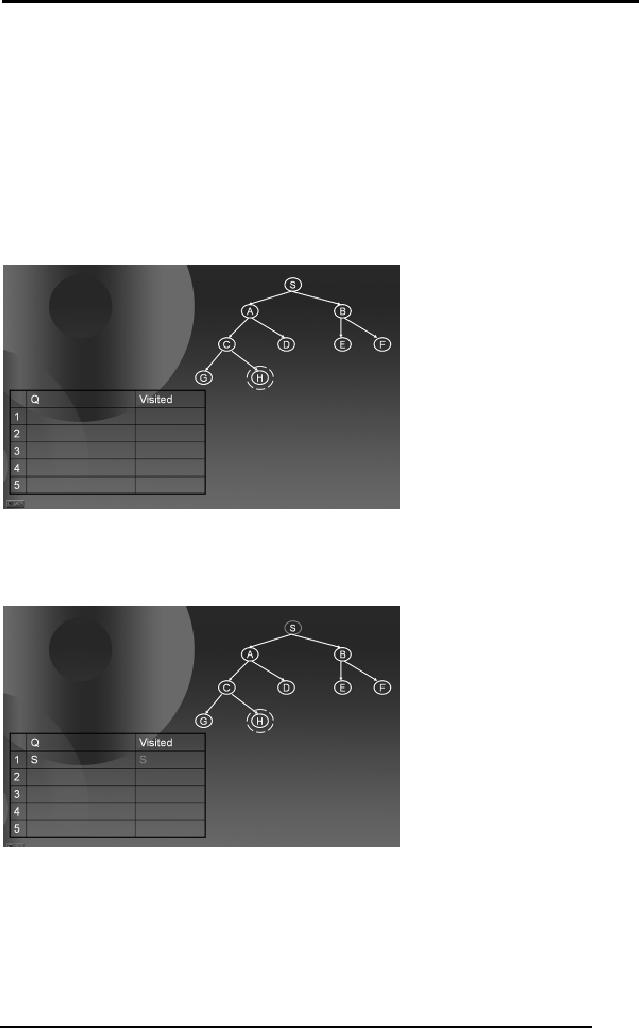
We start
with a tree containing nodes
S, A, B, C, D, E, F, G, and H, with H as
the
goal
node. In the bottom left
table we show the two
queues Q and Visited.
According to
the Simple Search Algorithm,
we initialize Q with the
start node S,
shown
below.
If Q is not
empty, pick the node X
with the minimum P(n)
(in this case S), as it
is
the
only node in Q. Check if X is
goal, (in this case X is
not the goal). Hence
find
all
the children of X not in
Visited and add them to Q
and Visited. Goto Step
2.
25
Artificial
Intelligence (CS607)
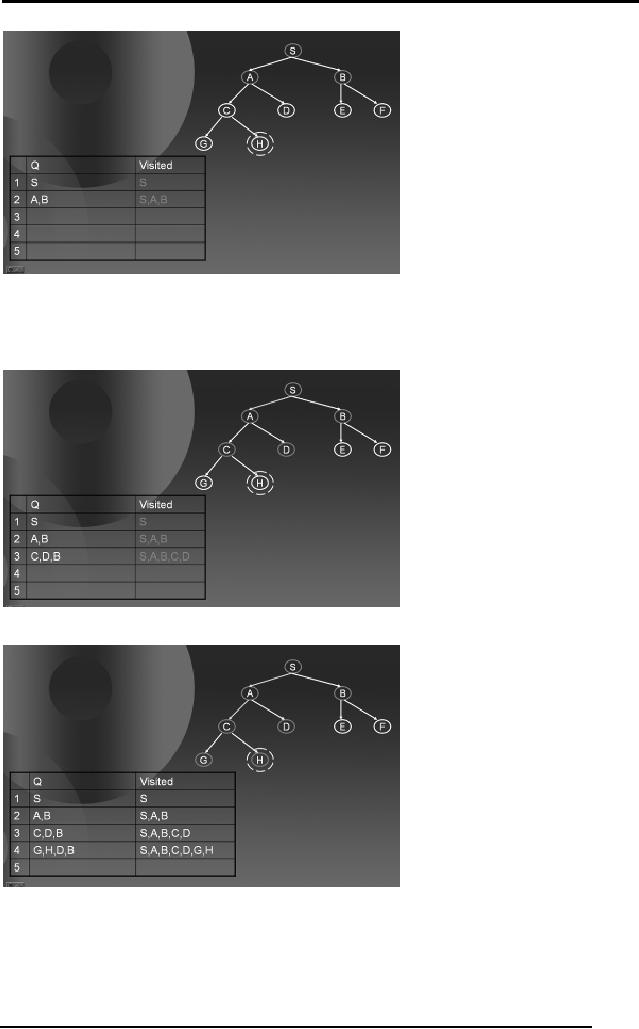
Again
check if Q is not empty,
pick the node X with
the minimum P(n) (in
this
case
either A or B), as both of
them have the same
value for P(n). Check if X
is
goal,
(in this case A is not
the goal). Hence, find
all the children of A not in
Visited
and add them to Q
and Visited. Go to Step 2.
Go on following
the steps in the Simple
Search Algorithm till you
find a goal node.
The diagrams
below show you how the
algorithm proceeds.
26
Artificial
Intelligence (CS607)
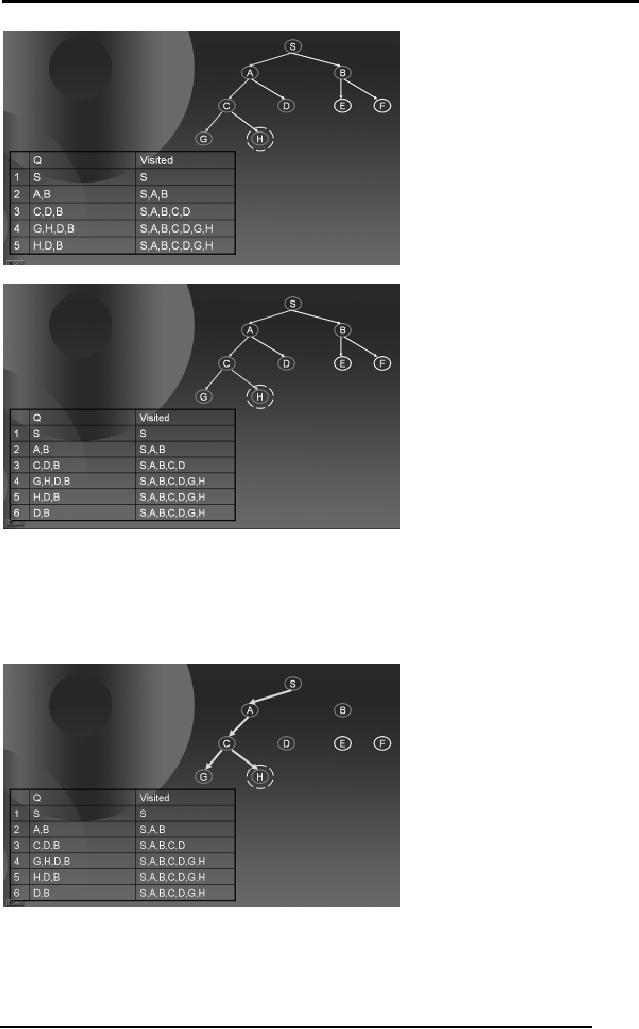
Here,
from the 5th row
of the table when we remove
H and check if it's the
goal,
the
algorithm says YES and hence we
return H as we have reached
the goal
state. The
path followed by the DFS is
shown by green arrows at
each step. The
diagram
below also shows that
DFS didn't have to search
the entire search
space,
rather only by traveling in
half the tree, the
algorithm was able to
search
the
solution.
Hence
simply by selecting a specific
P(n) our Simple Search
Algorithm was
converted to a
DFS procedure.
27
Artificial
Intelligence (CS607)
2.11 Simple
Search Algorithm Applied to Breadth First
Search
Breadth
First Search explores the
breadth of the tree first
and progresses
downward
level by level. Now, we will
use the same Simple
Search Algorithm to
implement
BFS by keeping our priority
function as
P(n) = height
(n)
As mentioned
previously, we will give
priority to the element with
minimum P(n)
hence
the node with the
largest value of height will
be at the maximum priority
to
be picked
from Q. In other
words, greater the
depth/height greater the
priority.
The following
sequence of diagrams will
show you how BFS works on a
tree
using
the Simple Search
Algorithm.
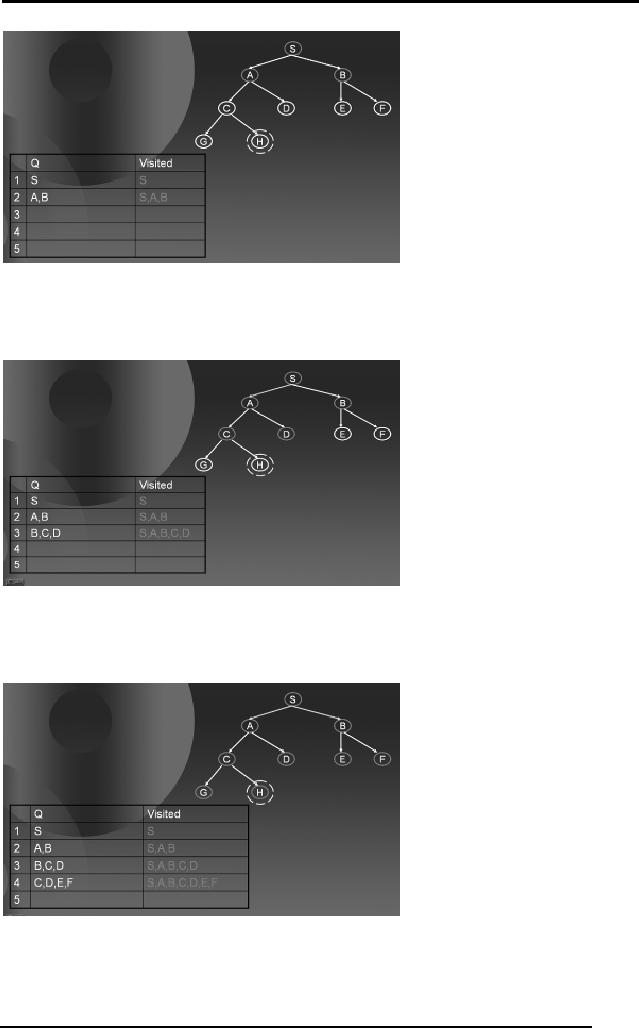
We start
with a tree containing nodes
S, A, B, C, D, E, F, G, and H, with H as
the
goal
node. In the bottom left
table we show the two
queues Q and Visited.
According to
the Simple Search Algorithm,
we initialize Q with the
start node S.
If Q is not
empty, pick the node X
with the minimum P(n)
(in this case S), as it
is
the
only node in Q. Check if X is
goal, (in this case X is
not the goal). Hence
find
all
the children of X not in
Visited and add them to Q
and Visited. Goto Step
2.
28
Artificial
Intelligence (CS607)
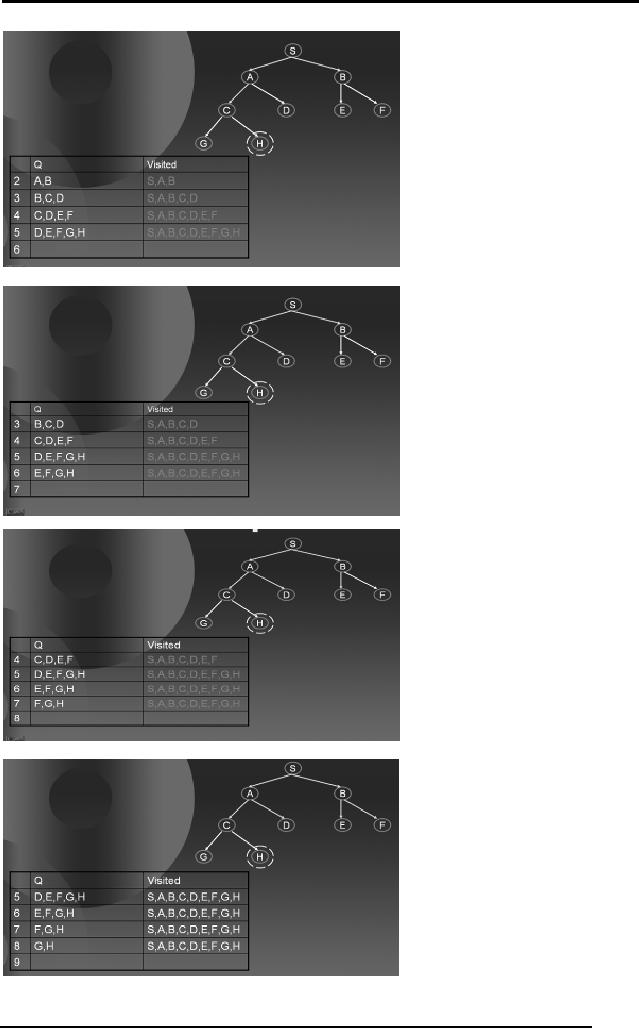
Again,
check if Q is not empty,
pick the node X with
the minimum P(n) (in
this
case
either A or B), as both of
them have the same
value for P(n). Remember,
n
refers to
the node X. Check if X is
goal, (in this case A is
not the goal). Hence
find
all
the children of A not in
Visited and add them to Q
and Visited. Go to Step
2.
Now, we
have B, C and D in the list
Q. B has height 1 while C and D
are at a
height 2. As we
are to select the node
with the minimum P(n)
hence we will select
B and
repeat. The following sequence of
diagram tells you how the
algorithm
proceeds
till it reach the goal
state.
29
Artificial
Intelligence (CS607)
30
Artificial
Intelligence (CS607)
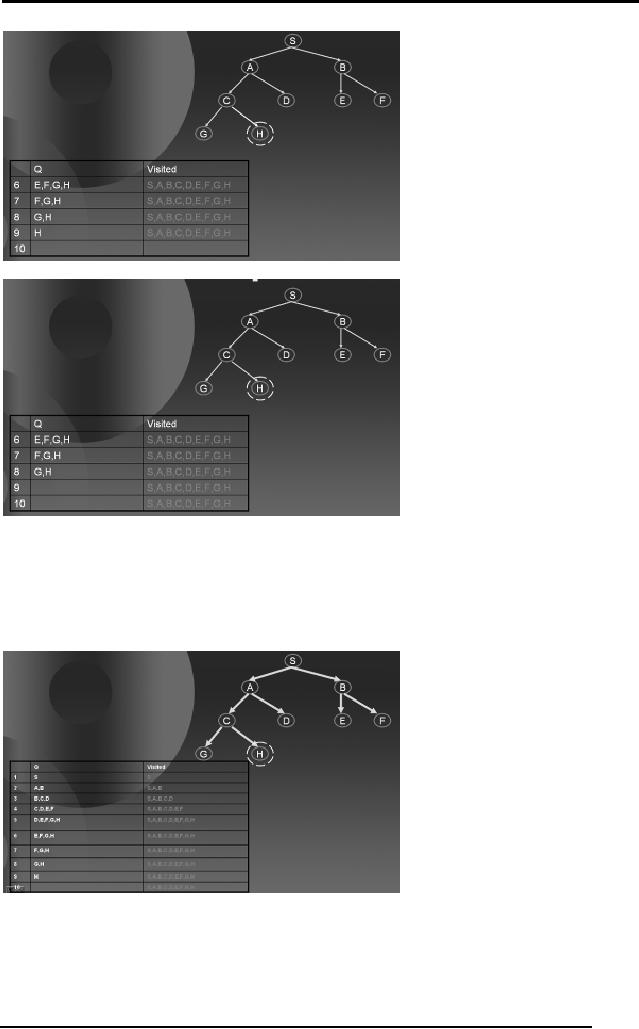
When we
remove H from the 9th row of the table and
check if it's the goal,
the
algorithm
says YES and hence we return H
since we have reached the
goal
state. The
path followed by the BFS is
shown by green arrows at
each step. The
diagram
below also shows that
BFS travels a significant
area of the search
space
if the
solution is located somewhere
deep inside the
tree.
Hence,
simply by selecting a specific
P(n) our Simple Search
Algorithm was
converted to a
BFS procedure.
31
Artificial
Intelligence (CS607)
2.12 Problems with
DFS and BFS
Though
DFS and BFS are
simple searching techniques
which can get us to
the
goal
state very easily yet
both of them have their
own problems.
DFS
has small space requirements
(linear in depth) but has
major problems:
DFS
can run forever in search
spaces with infinite length
paths
DFS
does not guarantee finding
the shallowest goal
BFS
guarantees finding the
shallowest path even in
presence of infinite
paths,
but it
has one great problem
BFS
requires a great deal of
space (exponential in
depth)
We can
still come up with a better
technique which caters for
the drawbacks of
both
these techniques. One such
technique is progressive
deepening.
2.13
Progressive Deepening
Progressive
deepening actually emulates BFS
using DFS. The idea is to
simply
apply
DFS to a specific level. If
you find the goal,
exit, other wise repeat
DFS to
the
next lower level. Go on
doing this until you either
reach the goal node or
the
full
height of the tree is
explored. For example, apply
a DFS to level 2 in the
tree,
if it reaches
the goal state, exit,
otherwise increase the level
of DFS and apply it
again
until you reach level 4. You
can increase the level of
DFS by any factor. An
example
will further clarify your
understanding.
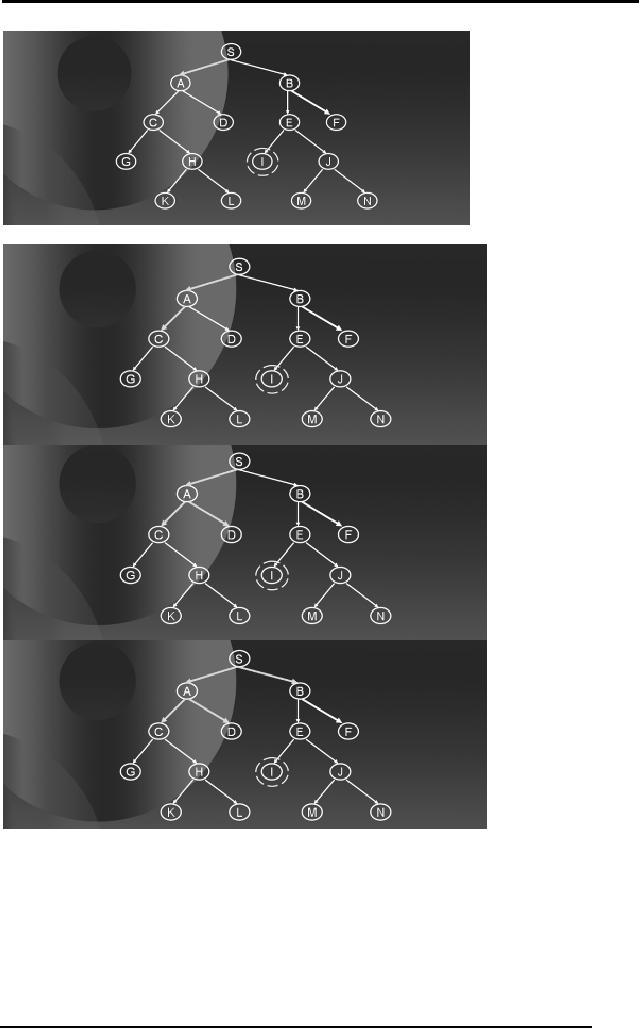
Consider
the tree on the previous
page with nodes from S ...
to N, where I is the
goal
node.
Apply
DFS to level 2 in the tree.
The green arrows in the
diagrams below show
how
DFS will proceed to level
2.
32
Artificial
Intelligence (CS607)
33
Artificial
Intelligence (CS607)
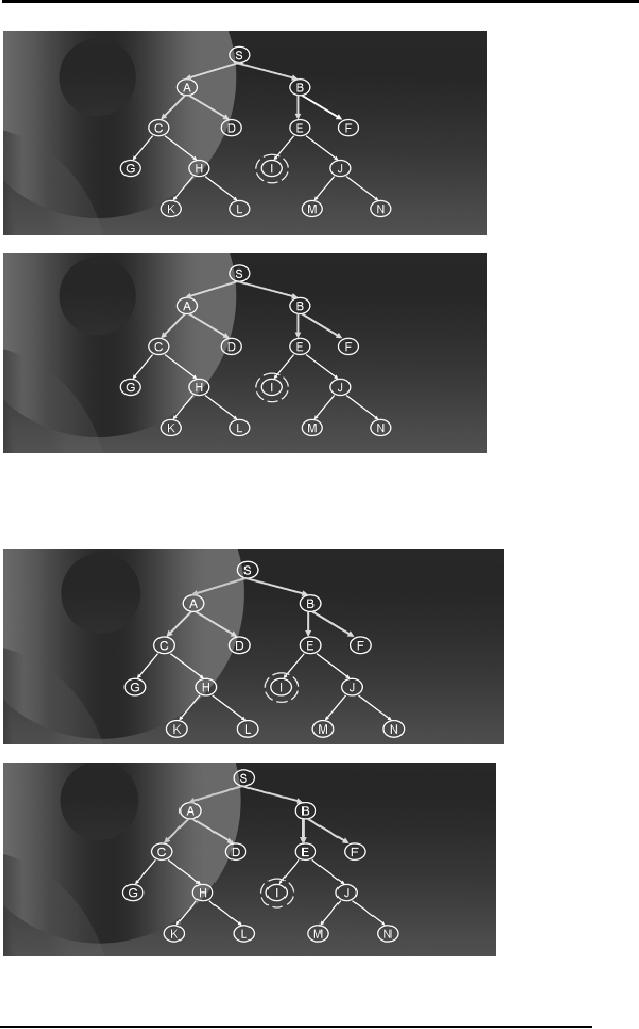
After
exploring to level 2, the
progressive deepening procedure
will find out
that
the
goal state has still
not been reached. Hence, it
will increment the level by
a
factor
of, say 2, and will
now perform a DFS in the
tree to depth 4. The
blue
arrows in
the diagrams below show
how DFS will proceed to
level 4.
34
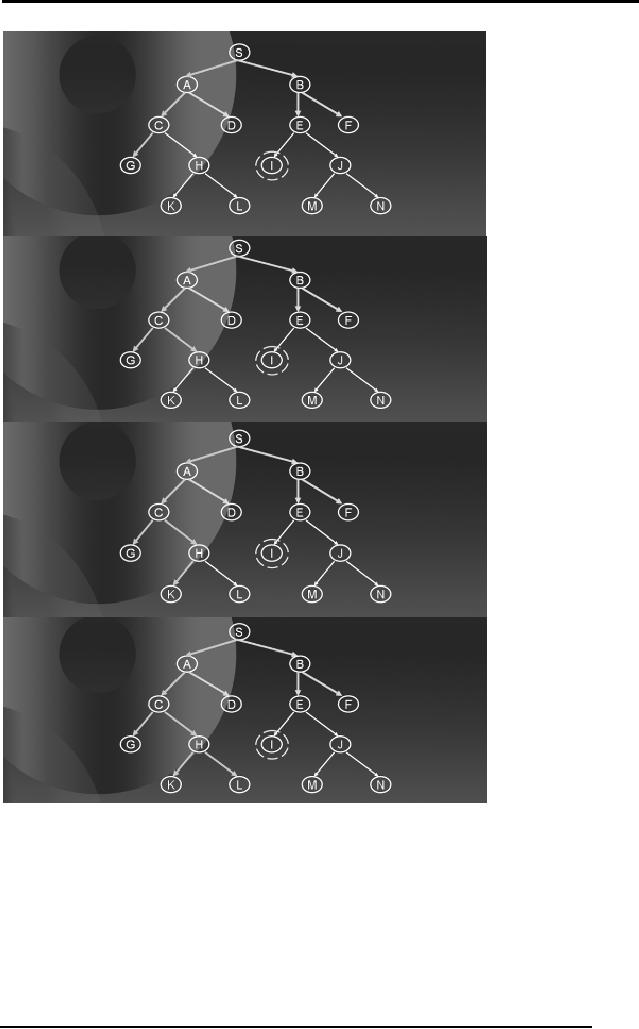
Artificial
Intelligence (CS607)
35
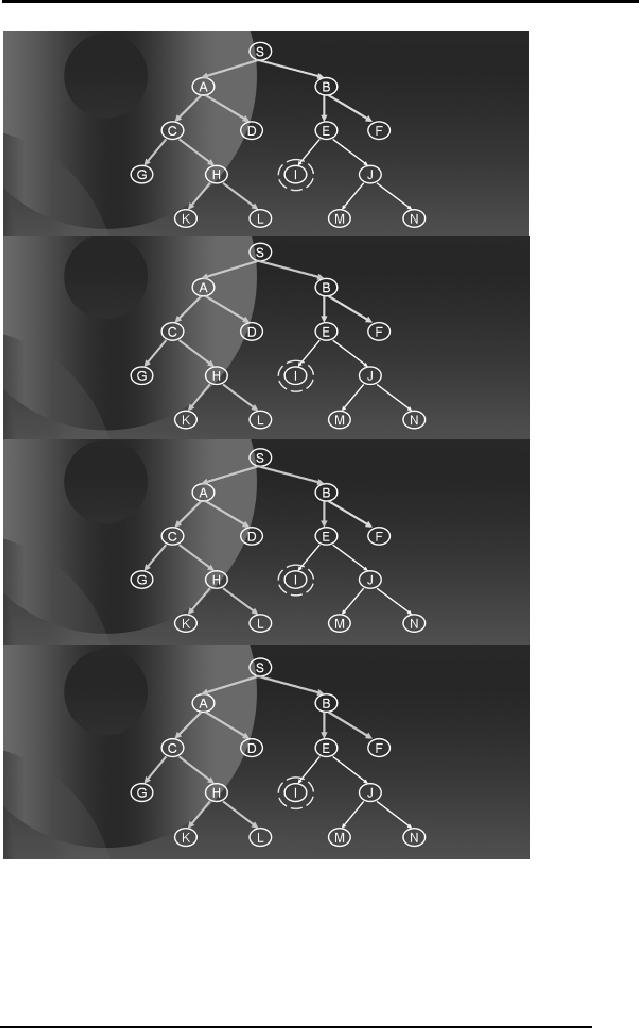
Artificial
Intelligence (CS607)
36

Artificial
Intelligence (CS607)
As soon as
the procedure finds the
goal state it will quit.
Notice that it
guarantees
to find
the solution at a minimum
depth like BFS. Imagine
that there are a
number
of solutions
below level 4 in the tree.
The procedure would only
travel a small
portion of
the search space and
without large memory
requirements, will find
out
the
solution.
2.14
Heuristically Informed Searches
So far we
have looked into procedures
that search the solution
space in an
uninformed
manner. Such procedures are
usually costly with respect
to either
time,
space or both. We now focus
on a few techniques that
search the solution
space in an
informed manner using
something which is called a
heuristic. Such
techniques
are called heuristic
searches. The basic idea of a
heuristic search is
that
rather than trying all
possible search paths, you
try and focus on paths
that
seem to be
getting you closer to your
goal state using some
kind of a "guide". Of
course, you
generally can't be sure that
you are really near
your goal state.
However, we
might be able to use a good
guess for the purpose.
Heuristics are
used to
help us make that guess. It
must be noted that
heuristics don't
always
give us
the right guess, and
hence the correct solutions.
In other words
educated
guesses
are not always
correct.
Recall
the example of the mouse
searching for cheese. The
smell of cheese
guides
the mouse in the maze, in
other words the strength of
the smell informs
the
mouse that how far is it
from the goal state.
Here the smell of cheese is
the
heuristic
and it is quite
accurate.
Similarly,
consider the diagram below.
The graph shows a map in
which the
numbers on
the edges are the
distances between cities,
for example, the
distance
between city S and city D is
3 and between B and E is 4.
37
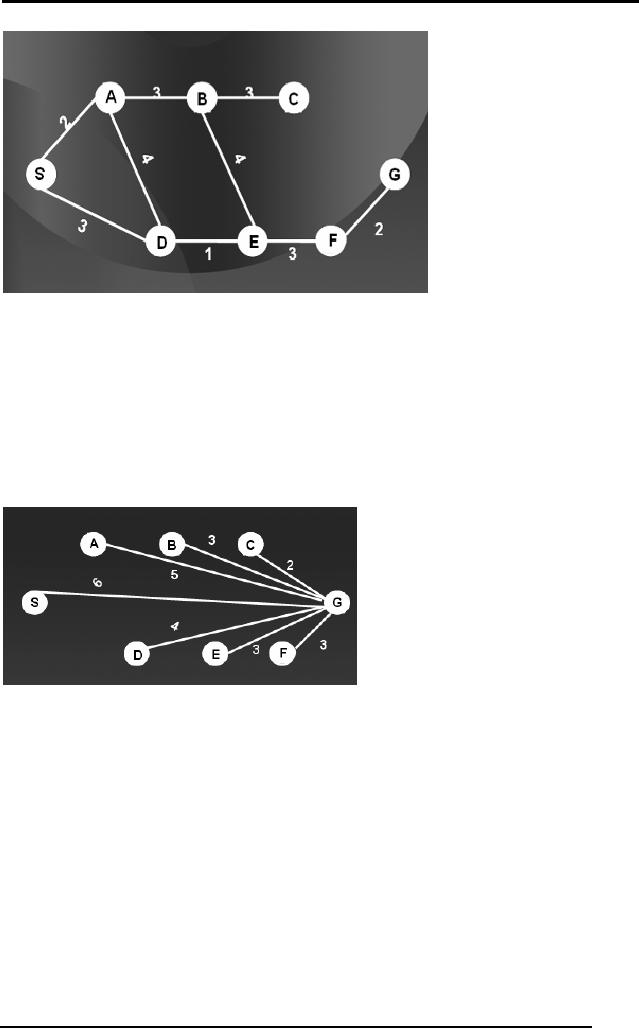
Artificial
Intelligence (CS607)
Suppose
our goal is to reach city G
starting from S. There can
be many choices,
we might
take S, A, D, E, F, G or travel from S,
to A, to E, to F, and to G. At
each
city, if we
were to decide which city to
go next, we might be interested in
some
sort of
information which will guide
us to travel to the city
from which the
distance
of goal is
minimum.
If someone
can tell us the
straight-line distance of G from
each city then it
might
help us as a
heuristic in order to decide
our route map. Consider
the graph
below.
It shows
the straight line distances
from every city to the
goal. Now, cities that
are
closer to
the goal should be our
preference. These straight
line distances also
known as
"as the crow flies
distance" shall be our
heuristic.
It is important to
note that heuristics can
sometimes misguide us. In
the example
we have
just discussed, one might
try to reach city C as it is
closest from the
goal
according to
our heuristic, but in the
original map you can see
that there is no
direct
link between city C and
city G. Even if someone
reaches city C using
the
heuristic, he
won't be able to travel to G
from C directly, hence the
heuristic can
misguide. The
catch here is that
crow-flight distances do not
tell us that the
two
cities
are directly
connected.
Similarly, in
the example of mouse and
cheese, consider that the
maze has
fences
fixed along some of the
paths through which the
smell can pass.
Our
heuristic
might guide us on a path
which is blocked by a fence,
hence again the
heuristic is
misguiding us.
38

Artificial
Intelligence (CS607)
The conclusion
then is that heuristics do
help us reduce the search
space, but it
is not at
all guaranteed that we'll
always find a solution.
Still many people
use
them as
most of the time they
are helpful. The key lies in
the fact that how do
we
use
the heuristic. Consider the
notion of a heuristic
function.
Whenever we
choose a heuristic, we come up
with a heuristic function
which
takes as
input the heuristic and
gives us out a number
corresponding to that
heuristic. The
search will now be guided by
the output of the heuristic
function.
Depending on
our application we might
give priority to either
larger numbers or
smaller
numbers.
Hence to
every node/ state in our
graph we will assign a
heuristic value,
calculated by
the heuristic function. We
will start with a basic
heuristically
informed
search which is called Hill
Climbing.
2.15
Hill Climbing
Hill
Climbing is basically a depth
first search with a measure
of quality that is
assigned to
each node in the tree. The
basic idea is: Proceed as
you would in
DFS
except that you order your
choices according to some
heuristic
measurement of
the remaining distance to
the goal. We will discuss
the Hill
climbing
with an example.
Before
going to the actual example,
let us give another analogy
for which the
name
Hill Climbing has been
given to this procedure.
Consider a blind
person
climbing a
hill. He can not see
the peak of the hill. The
best he can do is that
from
a given
point he takes steps in all
possible directions and
wherever he finds
that
a step
takes him higher he takes
that step and reaches a new,
higher point. He
goes on
doing this until all
possible steps in any direction
will take him higher
and
this
would be the peak, hence
the name hill climbing.
Notice that each step
that
we take,
gets us closer to our goal
which in this example is the
peak of a hill.
Such a
procedure might as well have
some problems.
Foothill Problem:
Consider
the diagram of a mountain
below. Before
reaching
the
global maxima, that is the
highest peak, the blind
man will encounter
local
maxima
that are the intermediate
peaks and before reaching
the maximum
height. At
each of these local maxima,
the blind man gets
the perception of
having
reached the global maxima as
none of the steps takes
him to a higher
point.
Hence he might just reach
local maxima and think
that he has reached
the
global
maxima. Thus getting stuck
in the middle of searching
the solution space.
39

Artificial
Intelligence (CS607)
Plateau
Problem: Similarly,
consider another problem as
depicted in the
diagram
below. Mountains where flat
areas called plateaus are
frequently
encountered
the blind person might
again get stuck.
When he
reaches the portion of a
mountain which is totally
flat, whatever step
he
takes
gives him no improvement in
height hence he gets
stuck.
Ridge Problem:
Consider
another problem; you are
standing on what seems
like
a knife
edge contour running
generally from northeast to
southwest. If you
take
step in one
direction it takes you lower, on
the other hand when you
step in some
other
direction it gives you no
improvement.
All
these problems can be mapped
to situations in our solution
space searching.
If we are at a
state and the heuristics of
all the available options
take us to a
lower
value, we might be at local
maxima. Similarly, if all
the available
heuristics
40

Artificial
Intelligence (CS607)
take us to no
improvement we might be at a plateau.
Same is the case with
ridge
as we can
encounter such states in our
search tree.
The solution to
all these problems is
randomness. Try taking
random steps in
random
direction of random length and you
might get out of the
place where you
are
stuck.
Example
Let us
now take you through an
example of searching a tree
using hill climbing
to
end out
discussion on hill
climbing.
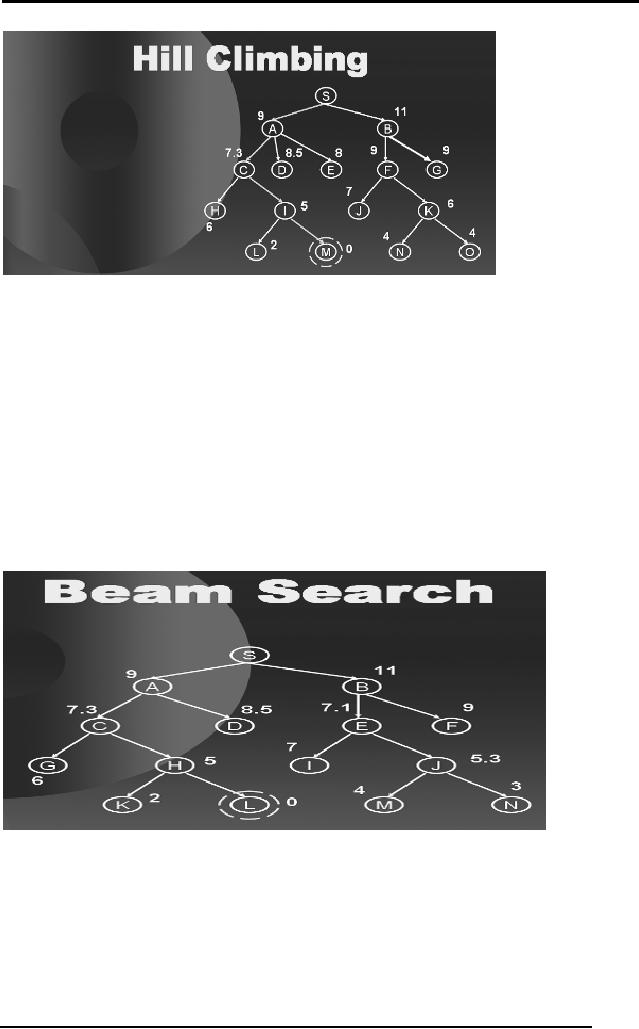
Consider
the diagram below. The tree
corresponds to our problem of
reaching
city M
starting from city S. In
other words our aim is to
find a path from S to
M.
We now
associate heuristics with
every node, that is the
straight line
distance
from
the path-terminating city to
the goal city.
When we
start at S we see that if we
move to A we will be left
with 9 units to
travel. As
moving on A has given us an
improvement in reaching our
goal hence
we move to A.
Exactly in the same manner
as the blind man moves up a
step
that
gives him more
height.
41
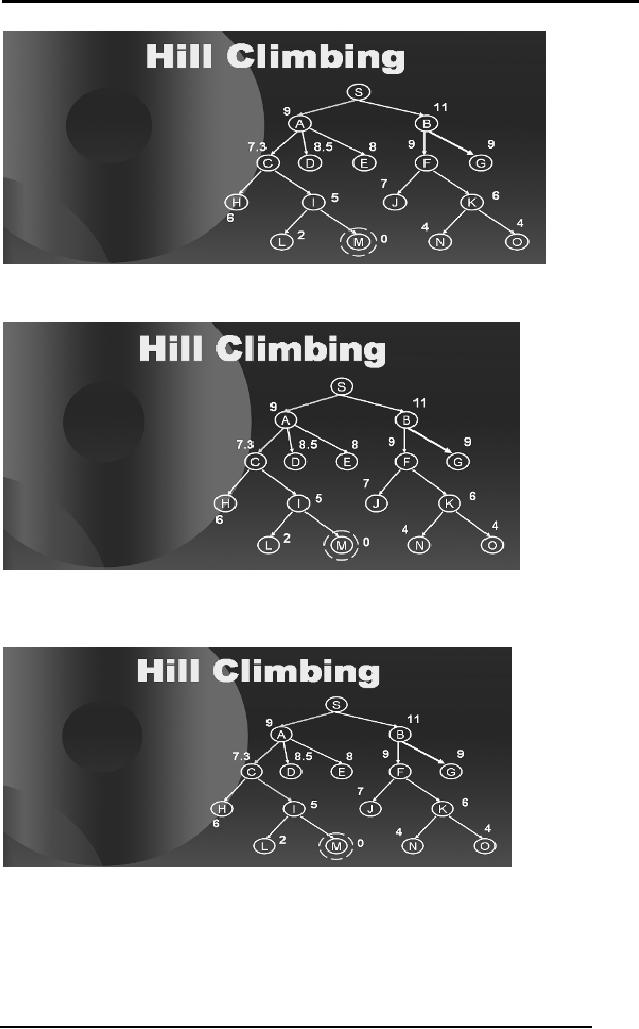
Artificial
Intelligence (CS607)
Standing on A we
see that C takes us closer
to the goal hence we move to
C.
From C we
see that city I give us
more improvement hence we
move to I and
then
finally to M.
42
Artificial
Intelligence (CS607)
Notice
that we only traveled a
small portion of the search
space and reached our
goal.
Hence the informed nature of
the search can help
reduce space and
time.
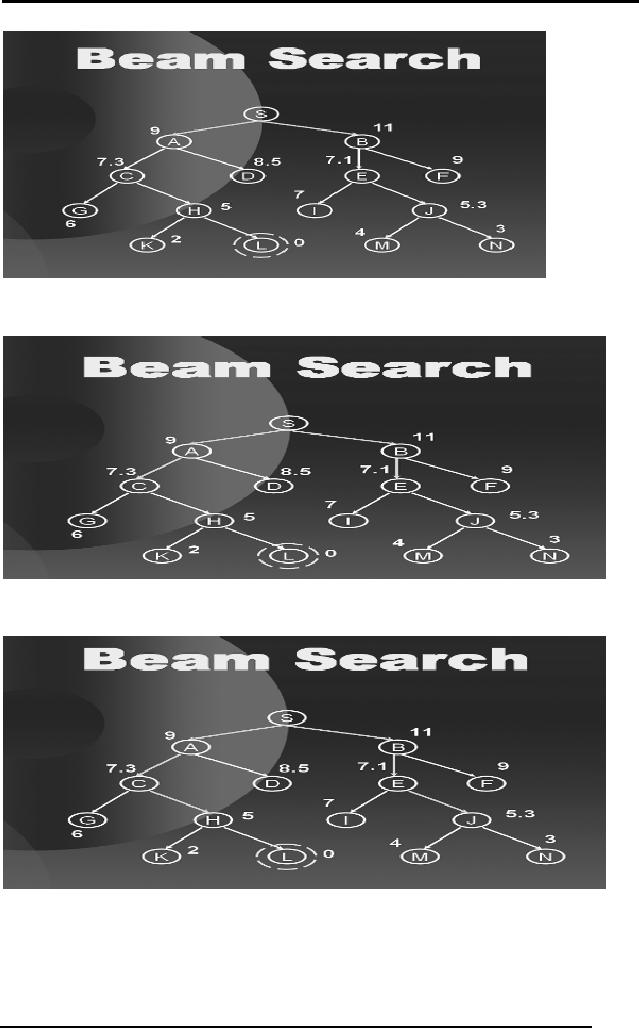
2.16 Beam
Search
You just
saw how hill climbing
procedure works through the
search space of a
tree.
Another procedure called
beam search proceeds in a
similar manner. Out
of
n possible
choices at any level, beam
search follows only the
best k of them; k is
the
parameter which we set and
the procedure considers only
those many nodes
at each
level.
The following
sequence of diagrams will
show you how Beam Search
works in a
search
tree.
We start
with a search tree with L as
goal state and k=2,
that is at every level
we
will
only consider the best 2
nodes. When standing on S we
observe that the
only
two
nodes available are A and B
so we explore both of them as
shown below.
43
Artificial
Intelligence (CS607)
From
here we have C, D, E and F as
the available options to go.
Again, we select
the
two best of them and we
explore C and E as shown in the
diagram below.
From C
and E we have G, H, I and J as
the available options so we
select H and
J and
similarly at the last level
we select L and N of which L is the
goal.
44

Artificial
Intelligence (CS607)
2.17 Best
First Search
Just as
beam search considers best k
nodes at every level, best
first search
considers
all the open nodes so
far and selects the best
amongst them. The
following
sequence of diagrams will
show you how a best first
search procedure
works in a
search tree.
We start
with a search tree as shown
above. From S we observe
that A is the
best
option so we explore A.
45

Artificial
Intelligence (CS607)
At A we now
have C, G, D and B as the
options. We select the best
of them
which is
D.
46

Artificial
Intelligence (CS607)
At D we have S, G,
B, H, M and J as the options. We
select H which is the best
of
them.
At last
from H we find L as the
best. Hence best first
search is a greedy
approach
will
looks for the best
amongst the available
options and hence can
sometimes
reduce
the searching time.
All these heuristically
informed procedures
are
considered
better but they do not
guarantee the optimal
solution, as they are
dependent on
the quality of heuristic
being used.
2.18 Optimal
Searches
So far we
have looked at uninformed
and informed searches. Both
have their
advantages and
disadvantages. But one thing
that lacks in both is that
whenever
they
find a solution they
immediately stop. They never
consider that their
might
be more
than one solution to the
problem and the solution
that they have
ignored
might be
the optimal one.
A simplest
approach to find the optimal
solution is this; find all
the possible
solutions
using either an uninformed
search or informed search
and once you
have
searched the whole search
space and no other solution
exists, then choose
47

Artificial
Intelligence (CS607)
the
most optimal amongst the
solutions found. This
approach is analogous to
the
brute
force method and is also
called the British museum
procedure.
But in
reality, exploring the
entire search space is never
feasible and at times
is
not
even possible, for instance,
if we just consider the tree
corresponding to a
game of
chess (we will learn
about game trees later),
the effective
branching
factor is 16 and
the effective depth is 100.
The number of branches in an
exhaustive
survey would be on the order
of 10120.
Hence a huge amount
of
computation
power and time is required in
solving the optimal search
problems in
a brute
force manner.
2.19 Branch and
Bound
In order to
solve our problem of optimal
search without using a brute
force
technique,
people have come up with
different procedures. One such
procedure
is called
branch-and-bound method.
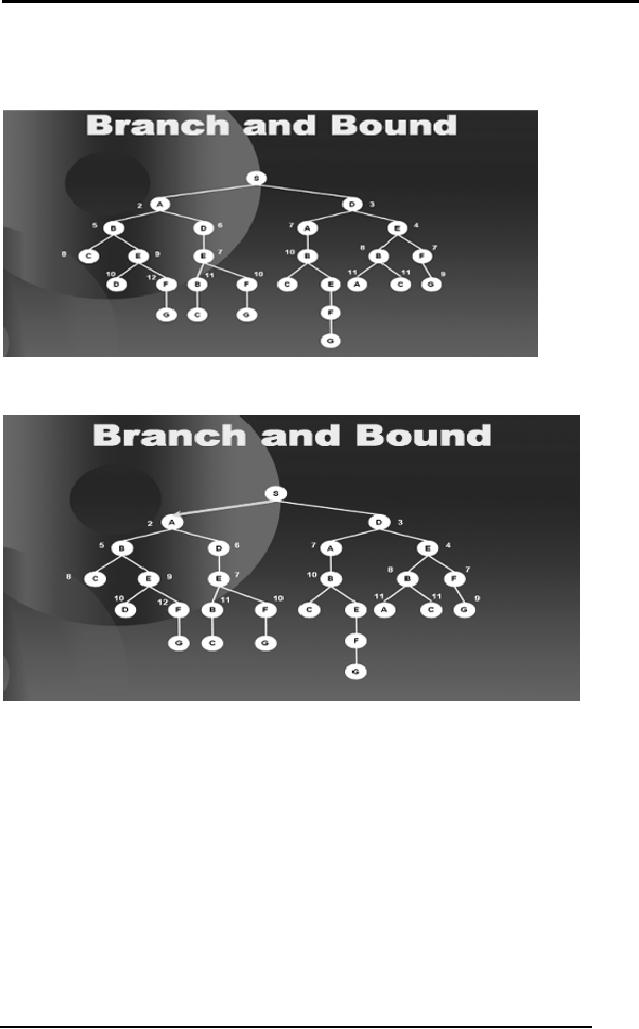
The simple
idea of branch and bound is
the following:
The length of
the complete path from S to
G is 9. Also note that while
traveling
from S to B we
have already covered a
distance of 9 units. So traveling
further
from S D A B to
some other node will
make the path longer. So we
ignore any
further
paths ahead of the path S D
A B.
We will
show this with a simple
example.
48
Artificial
Intelligence (CS607)
The diagram
above shows the same
city road map with
distance between the
cities
labels on the edges. We
convert the map to a tree as
shown below.
We proceed in a
Best First Search manner.
Starting at S we see that A is
the
best
option so we explore A.
From S
the options to travel are B
and D, the children of A and
D the child of S.
Among
these, D the child of S is
the best option. So we
explore D.
49
Artificial
Intelligence (CS607)
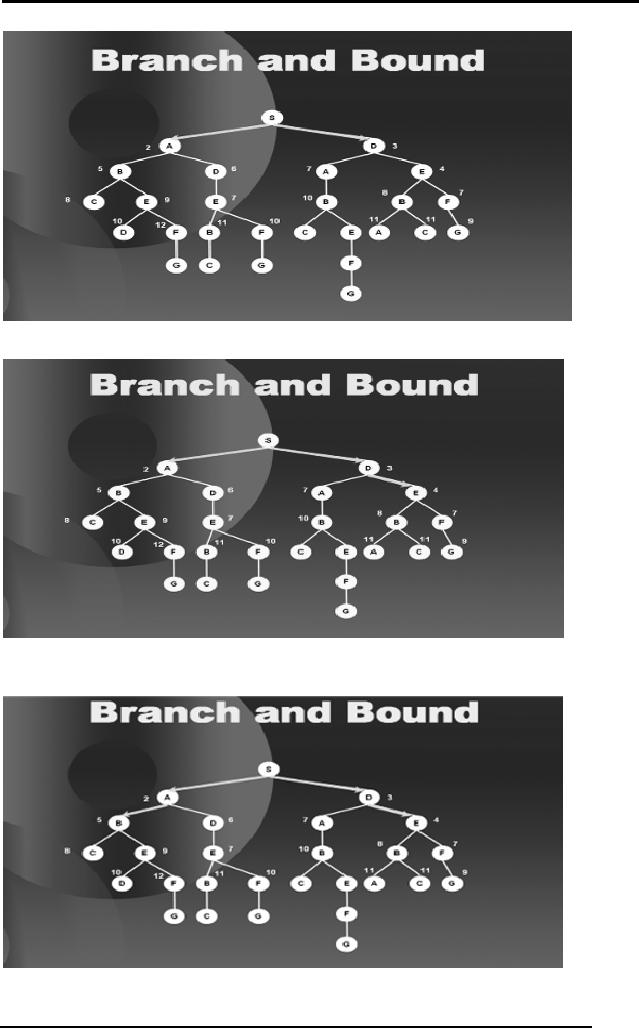
From
here the best option is E so
we go there,
then
B,
then
D,
50
Artificial
Intelligence (CS607)
Here we
have E, F and A as equally good
options so we select arbitrarily
and
move to
say A,
then
E.
51
Artificial
Intelligence (CS607)
When we
explore E we find out that
if we follow this path
further, our path
length
will
increase beyond 9 which is
the distance of S to G. Hence we
block all the
further
sub-trees along this path,
as shown in the diagram
below.
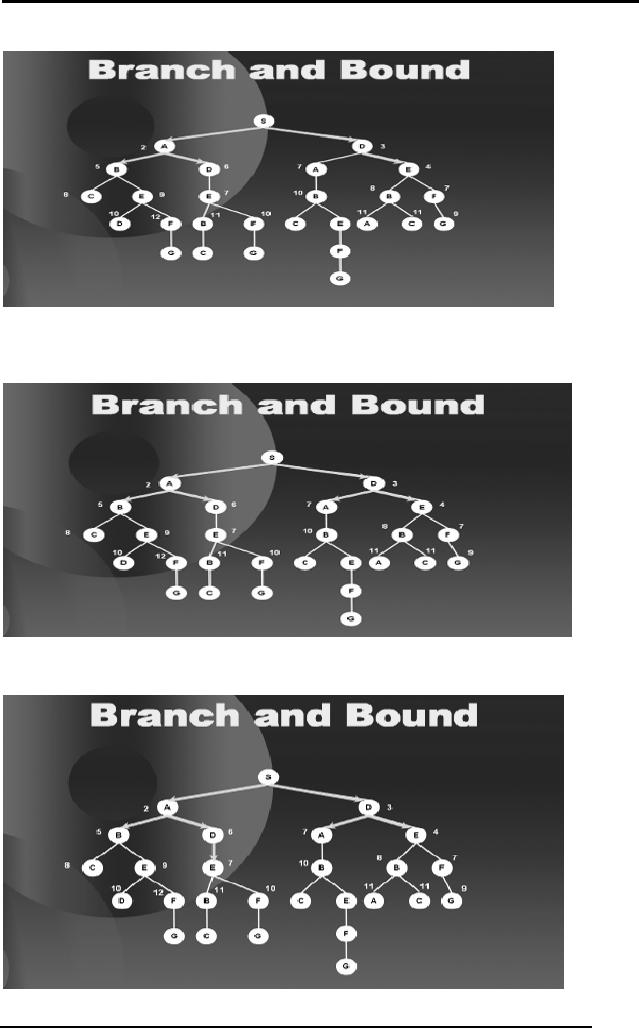
We then
move to F as that is the
best option at this point
with a value 7.
then
C,
We see
that C is a leaf node so we
bind C too as shown in the
next diagram.
52
Artificial
Intelligence (CS607)
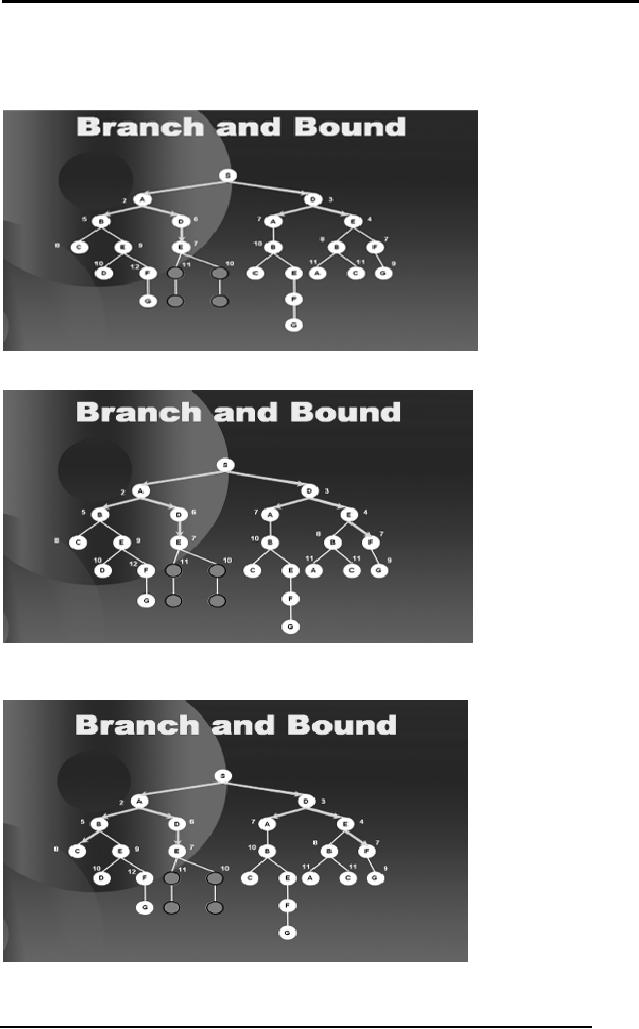
Then we
move to B on the right hand
side of the tree and
bind the sub
trees
ahead of B as
they also exceed the
path length 9.
53
Artificial
Intelligence (CS607)
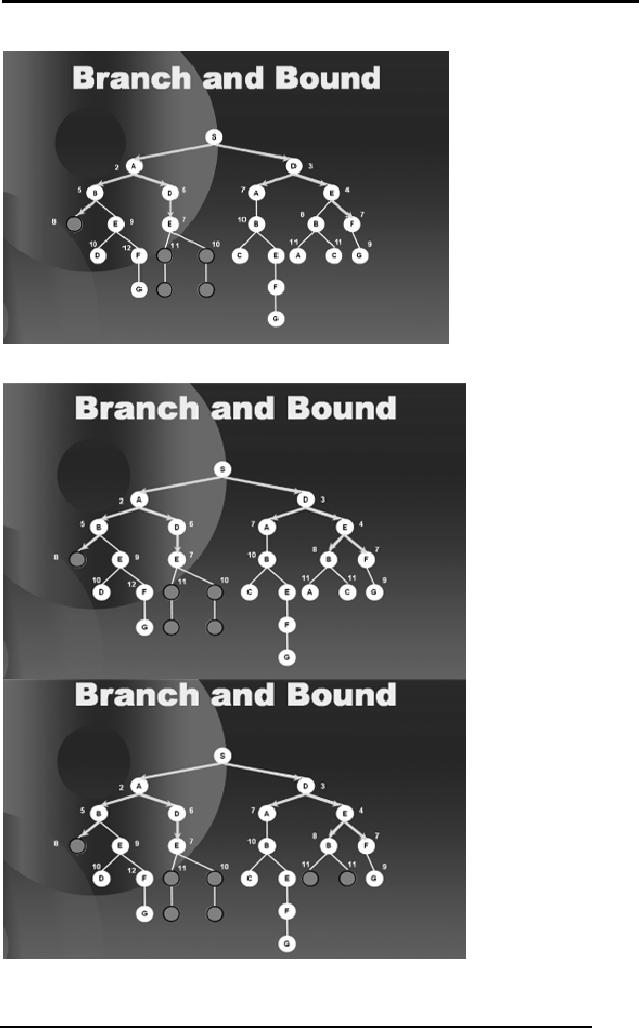
We go on
proceeding in this fashion,
binding the paths that
exceed 9 and hence
we are
saved from traversing a
considerable portion of the
tree. The subsequent
diagrams
complete the search until it
has found all the
optimal solution, that
is
along
the right hand branch of
the tree.
54

Artificial
Intelligence (CS607)
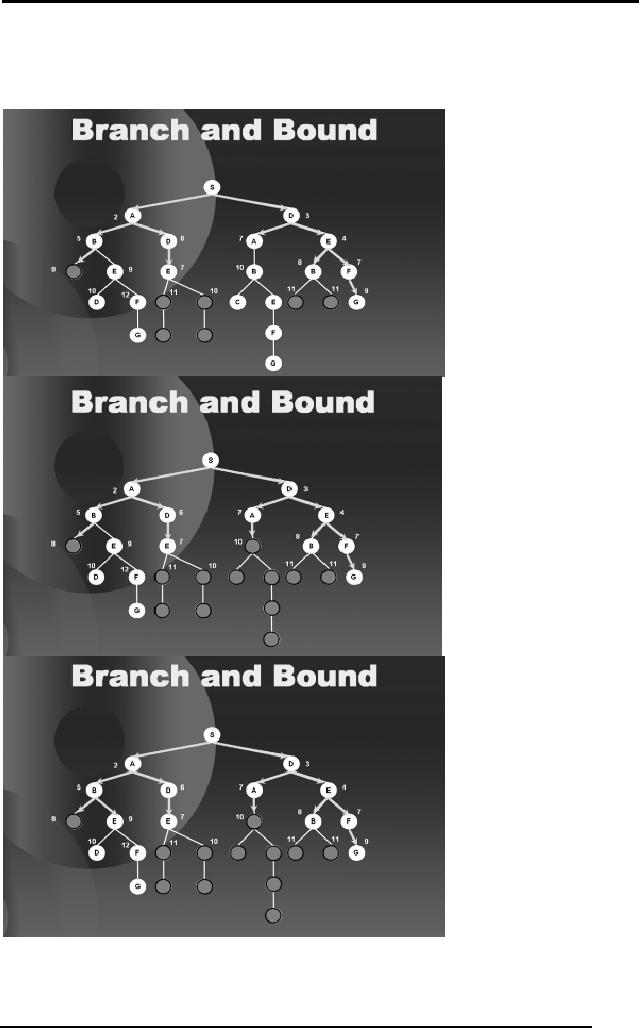
Notice
that we have saved ourselves
from traversing a considerable
portion of
the
tree and still have
found the optimal solution.
The basic idea was to
reduce
the
search space by binding the
paths that exceed the
path length from S to
G.
2.20 Improvements
in Branch and Bound
The above
procedure can be improved in
many different ways. We will
discuss
the
two most famous ways to
improve it.
1.
Estimates
2. Dynamic
Programming
The idea of
estimates is that we can
travel in the solution space
using a heuristic
estimate. By
using "guesses" about
remaining distance as well as
facts about
distance
already accumulated we will be
able to travel in the
solution space more
efficiently.
Hence we use the estimates
of the remaining distance. A
problem
here is
that if we go with an overestimate of
the remaining distance then
we might
loose a
solution that is somewhere
nearby. Hence we always
travel with
underestimates of
the remaining distance. We
will demonstrate this
improvement
with an
example.
The second
improvement is dynamic programming.
The simple idea
behind
dynamic
programming is that if we can
reach a specific node
through more than
one different
path then we shall take
the path with the
minimum cost.
55
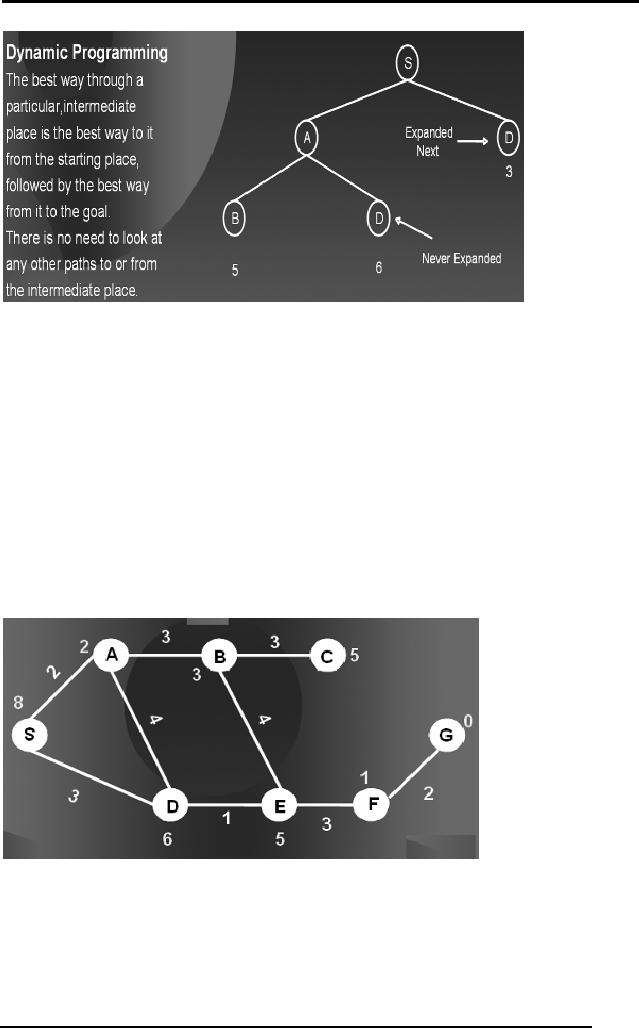
Artificial
Intelligence (CS607)
In the
diagram you can see
that we can reach node D
directly from S with a
cost
of 3 and via S A D
with a cost of 6 hence we
will never expand the
path with the
larger
cost of reaching the same
node.
When we
include these two
improvements in branch and bound
then we name it
as a different
technique known as A*
Procedure.
2.21 A*
Procedure
This is
actually branch and bound
technique with the
improvement of
underestimates
and dynamic
programming.
We will
discuss the technique with
the same example as that in
branch-and-
bound.
The values on
the nodes shown in yellow
are the underestimates of
the distance
of a specific
node from G. The values on
the edges are the
distance between two
adjacent
cities.
56
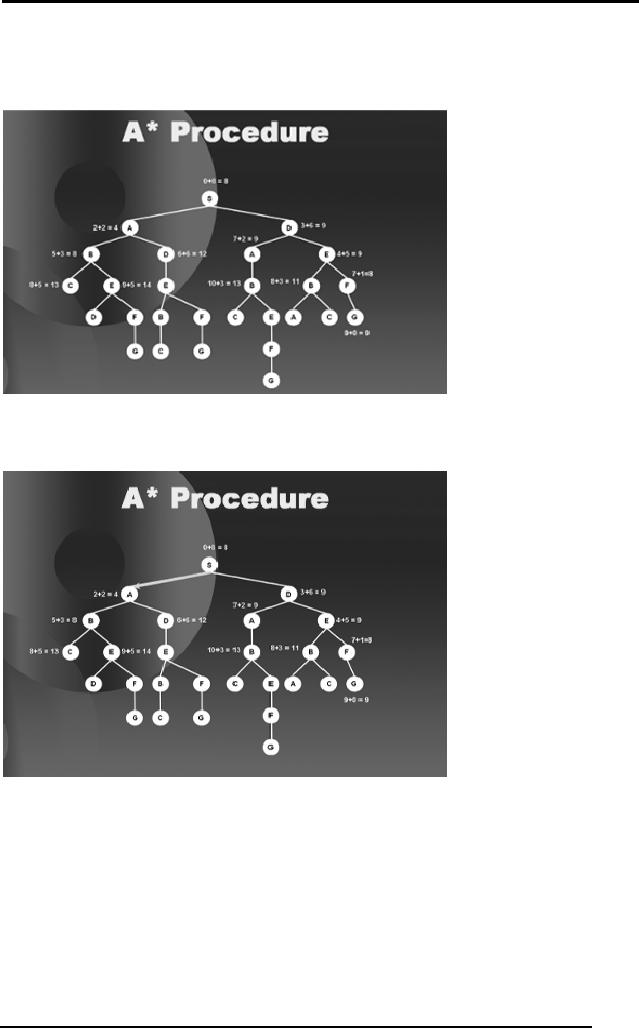
Artificial
Intelligence (CS607)
Our
measure of goodness and badness of a
node will now be decided by
a
combination of
values that is the distance
traveled so far and the
estimate of the
remaining
distance. We construct the
tree corresponding to the
graph above.
We start
with a tree with goodness of
every node mentioned on
it.
Standing at S we
observe that the best
node is A with a value of 4 so we
move to
4.
Then B. As
all the sub-trees emerging
from B make our path
length more than 9
units so we
bound this path, as shown in
the next diagram.
57
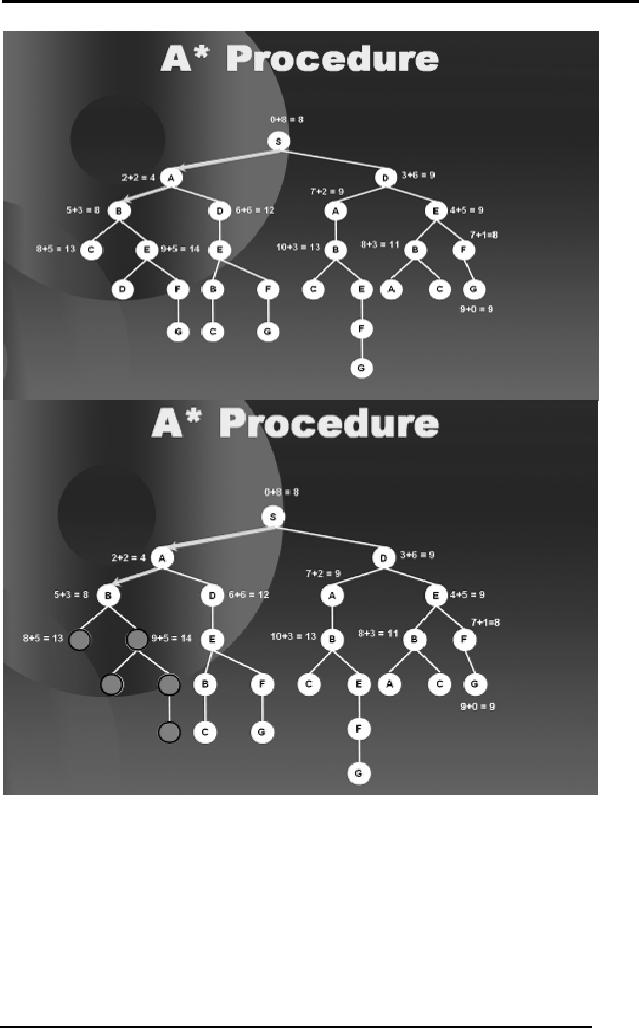
Artificial
Intelligence (CS607)
Now observe
that to reach node D that is
the child of A we can reach
it either with
a cost of 12 or we
can directly reach D from S
with a cost of 9. Hence
using
dynamic
programming we will ignore
the whole sub-tree beneath D
(the child of
A) as shown in
the next diagram.
58
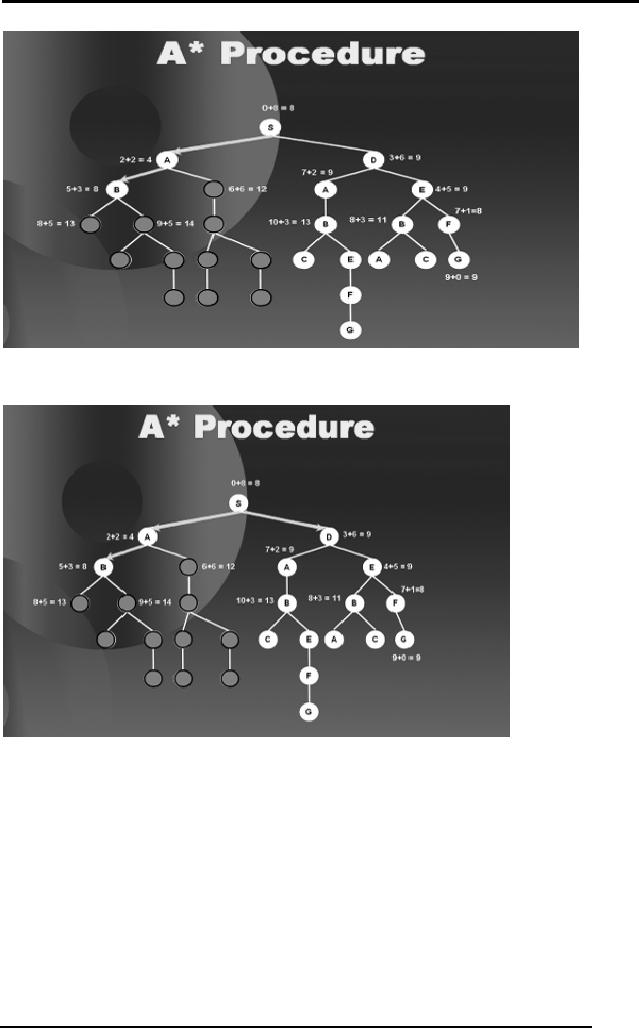
Artificial
Intelligence (CS607)
Now we move to D
from S.
Now A and E
are equally good nodes so we
arbitrarily choose amongst
them,
and we move to
A.
59
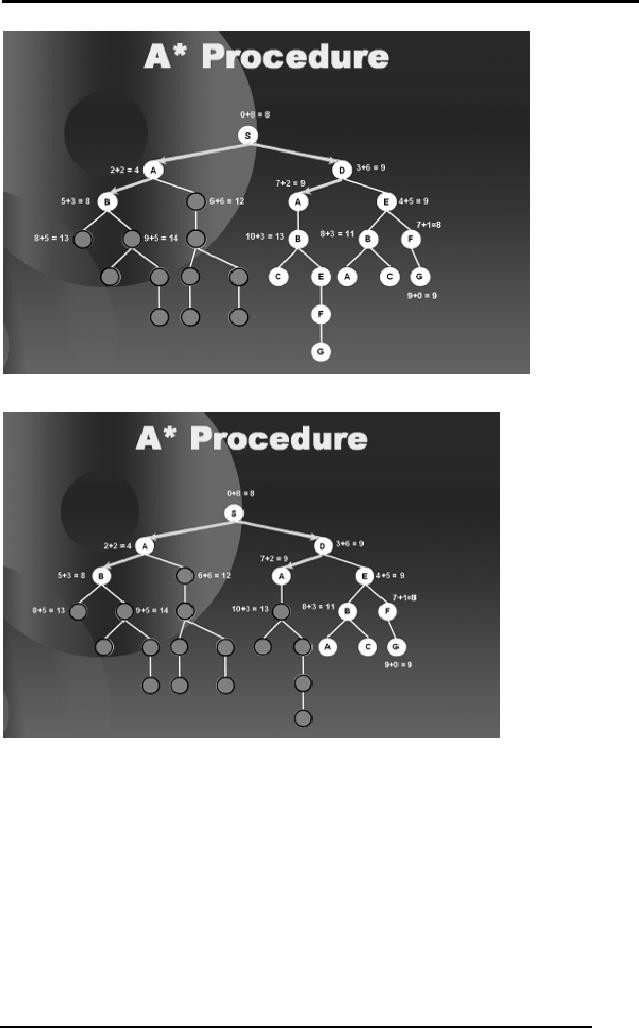
Artificial
Intelligence (CS607)
As the
sub-tree beneath A expands
the path length is beyond 9
so we bind it.
We proceed in
this manner. Next we visit
E, then we visit B the child
of E, we
bound
the sub-tree below B. We
visit F and finally we reach
G as shown in the
subsequent
diagrams.
60
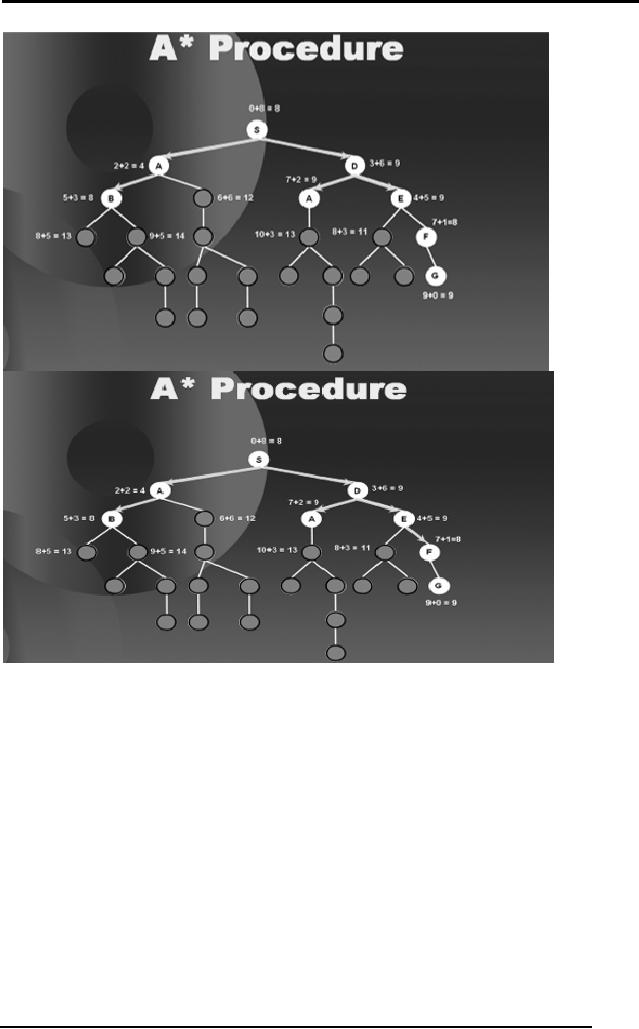
Artificial
Intelligence (CS607)
61
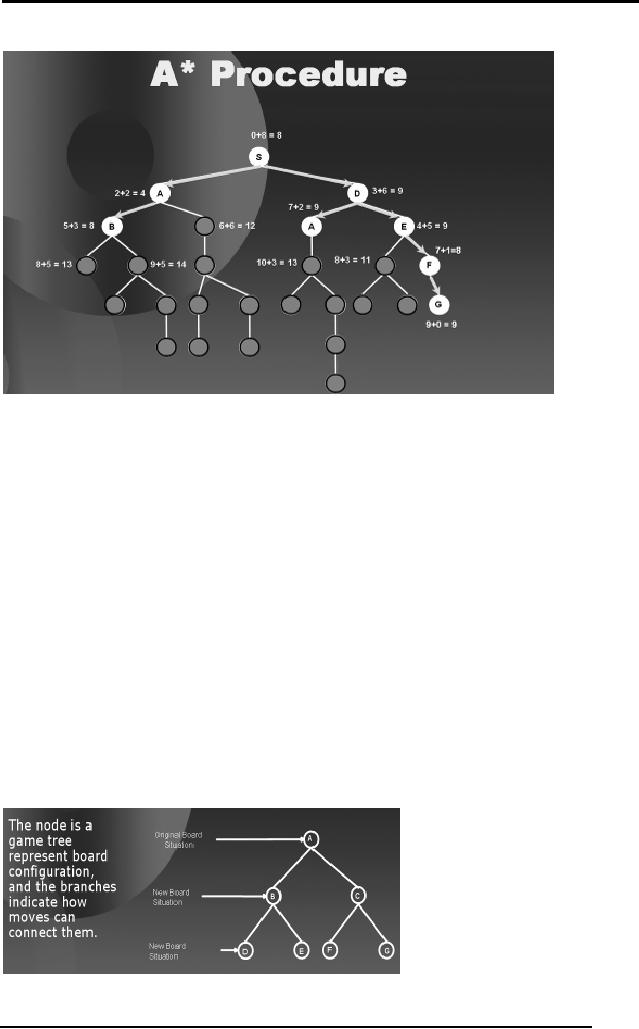
Artificial
Intelligence (CS607)
Notice
that by using underestimates and
dynamic programming the
search space
was
further reduced and our
optimal solution was found
efficiently.
2.22
Adversarial Search
Up until now
all the searches that we
have studied there was
only one person or
agent
searching the solution space
to find the goal or the
solution. In many
applications
there might be multiple
agents or persons searching
for solutions in
the
same solution space.
Such
scenarios usually occur in
game playing where two
opponents also called
adversaries
are searching for a goal.
Their goals are usually
contrary to each
other.
For example, in a game of
tic-tac-toe player one might
want that he should
complete a
line with crosses while at
the same time player
two wants to complete
a line of
zeros. Hence both have
different goals. Notice
further that if player
one
puts a
cross in any box, player-two
will intelligently try to
make a move that
would
leave
player-one with minimum
chance to win, that is, he
will try to stop
player-
one from
completing a line of crosses and at
the same time will
try to complete
his
line of zeros.
Many games
can be modeled as trees as
shown below. We will focus
on board
games
for simplicity.
62
Artificial
Intelligence (CS607)
Searches in
which two or more players
with contrary goals are
trying to explore
the
same solution space in
search of the solution are
called adversarial
searches.
2.23 Minimax
Procedure
In adversarial
searches one player tries to
cater for the opponent's
moves by
intelligently
deciding that what will be
the impact of his own
move on the over
all
configuration of
the game. To develop this
stance he uses a look ahead
thinking
strategy.
That is, before making a
move he looks a few levels
down the game
tree to
see that what can be
the impact of his move and
what options will be
open
to the
opponent once he has made
this move.
To clarify
the concept of adversarial
search let us discuss a
procedure called the
minimax
procedure.
Here we
assume that we have a
situation analyzer that
converts all
judgments
about
board situations into a
single, over all quality
number. This
situation
analyzer is
also called a static
evaluator and the score/
number calculated by
the
evaluator is
called the static evaluation
of that node. Positive
numbers, by
convention
indicate favor to one
player. Negative numbers
indicate favor to the
other
player. The player hoping
for positive numbers is
called maximizing
player
or maximizer. The
other player is called
minimizing player or minimizer.
The
maximizer
has to keep in view that
what choices will be
available to the
minimizer
on the
next step. The minimizer has
to keep in view that what
choices will be
available to
the maximizer on the next
step.
Consider
the following
diagram.
63

Artificial
Intelligence (CS607)
Standing at
node A the maximizer wants
to decide which node to
visit next, that
is,
choose between B or C. The maximizer
wishes to maximize the score
so
apparently 7
being the maximum score,
the maximizer should go to C
and then to
G. But
when the maximizer will
reach C the next turn to
select the node will be
of
the
minimizer, which will force
the game to reach
configuration/node F with a
score of 2.
Hence maximizer will end up
with a score of 2 if he goes to C
from A.
On the
other hand, if the maximizer
goes to B from A the worst
which the
minimizer
can do is that he will force
the maximizer to a score of 3.
Now, since
the
choice is between scores of 3 or 2,
the maximizer will go to
node B from A.
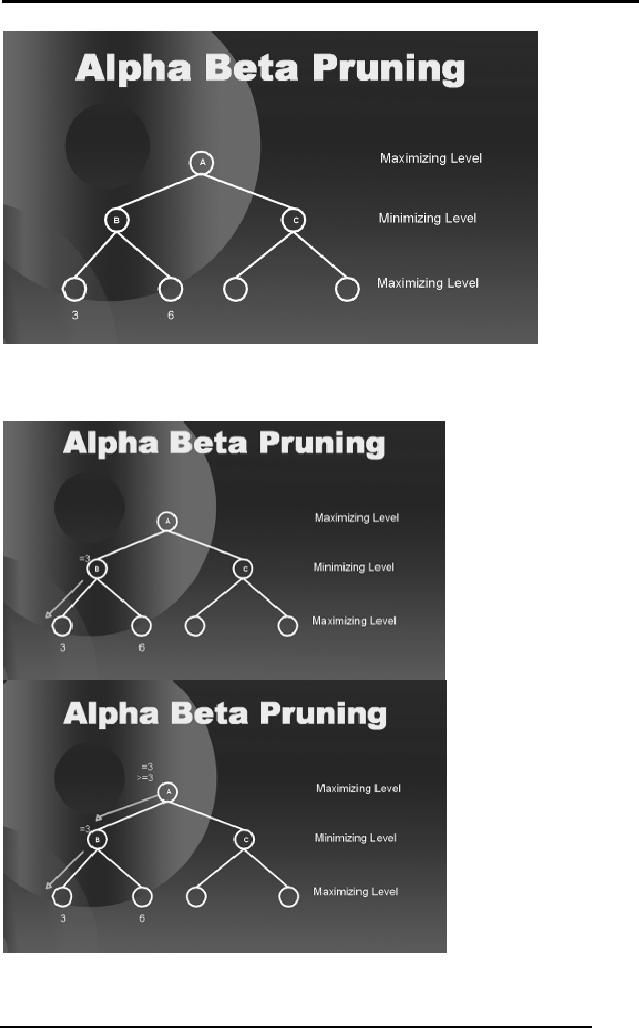
2.24 Alpha
Beta Pruning
In Minimax
Procedure, it seems as if the
static evaluator must be
used on each
leaf
node. Fortunately there is a
procedure that reduces both
the tree branches
that
must be generated and the
number of evaluations. This
procedure is called
Alpha
Beta pruning which "prunes"
the tree branches thus
reducing the number
of static
evaluations.
We use
the following example to
explain the notion of Alpha
Beta Pruning.
Suppose we
start of with a game tree in
the diagram below. Notice
that all
nodes/situations
have not yet been
previously evaluated for
their static
evaluation
score.
Only two leaf nodes
have been evaluated so
far.
64
Artificial
Intelligence (CS607)
Sitting at A,
the player-one will observe
that if he moves to B the
best he can get
is 3.
65
Artificial
Intelligence (CS607)
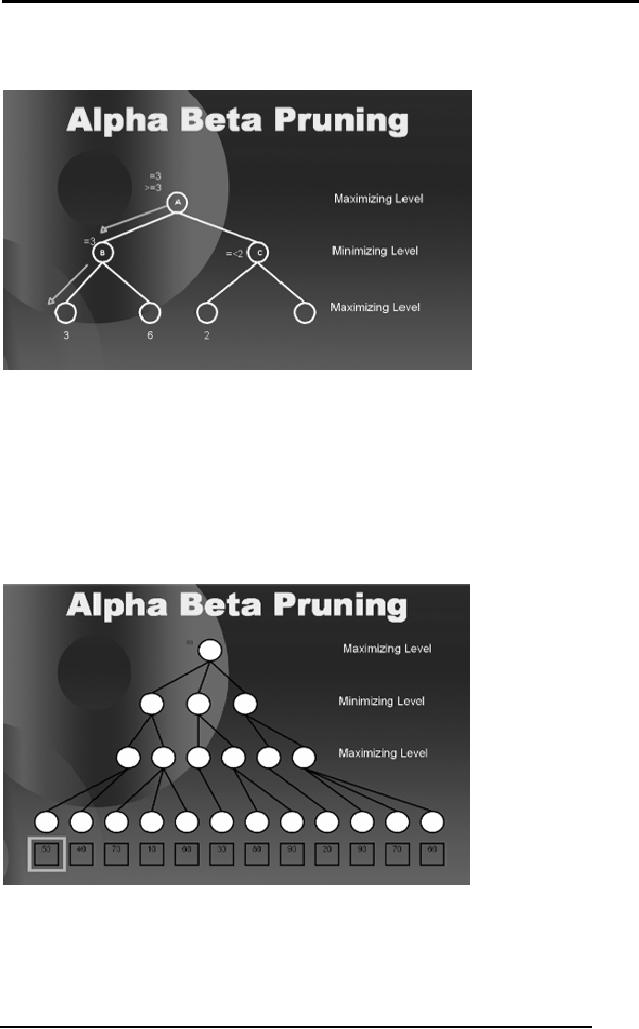
So the
value three travels to the
root A. Now after observing
the other side of
the
tree,
this score will either
increase or will remain the
same as this level is for
the
maximizer.
When he
evaluates the first leaf
node on the other side of
the tree, he will
see
that
the minimizer can force
him to a score of less than
3 hence there is no
need
to fully
explore the tree from
that side. Hence the
right most branch of the
tree will
be pruned and
won't be evaluated for
static evaluation.
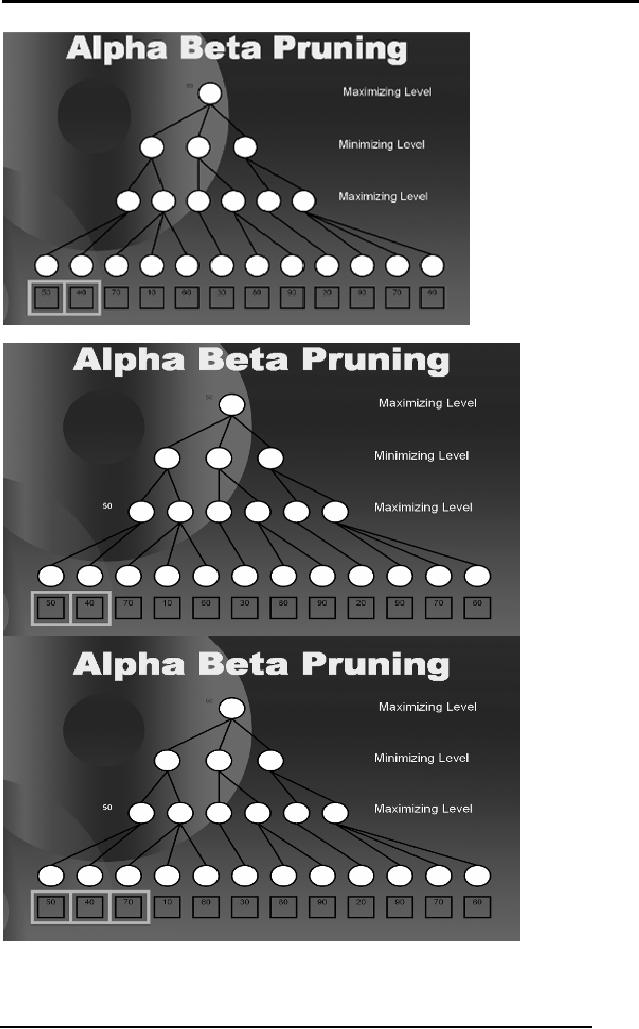
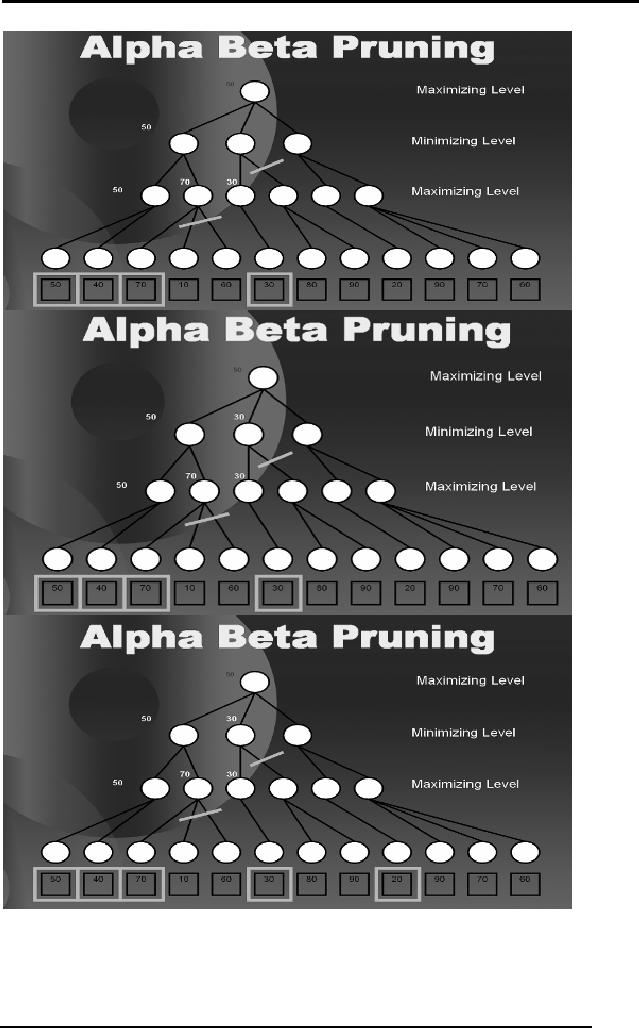
We have
discussed a detailed example on
Alpha Beta Pruning in the
lectures.
We have
shown the sequence of steps
in the diagrams below. The
readers are
required to go
though the last portion of
Lecture 10 for the
explanation of this
example, if
required.
66
Artificial
Intelligence (CS607)
67

Artificial
Intelligence (CS607)
68

Artificial
Intelligence (CS607)
69
Artificial
Intelligence (CS607)
70

Artificial
Intelligence (CS607)
2.25
Summary
People
used to think that one
who can solve more
problems is more
intelligent
71
Artificial
Intelligence (CS607)
Generate and
test is the classical
approach to solving
problems
Problem
representation plays a key role in
problem solving
The
components of problem solving
include
o Problem
Statement
o Operators
o Goal
State
o Solution
Space
Searching is a
formal mechanism to explore
alternatives
Searches
can be blind or uninformed,
informed, heuristic, non-optimal
and
optional.
Different
procedures to implement different
search strategies form the
major
content of
this chapter
2.26
Problems
Q1 Consider
that a person has never
been to the city air
port. Its early in
the
morning
and assume that no other
person is awake in the town
who can guide
him on
the way. He has to drive on
his car but doesn't
know the way to air
port.
Clearly
identify the four components
of problem solving in the
above statement,
i.e.
problem statement, operators,
solution space, and goal
state. Should he
follow
blind or heuristic search
strategy? Try to model the
problem in a graphical
representation.
Q2 Clearly
identify the difference
between WSP (Well-Structured
Problems) and
ISP (Ill-
Structured) problems as discussed in
the lecture. Give
relevant
examples.
Q3 Given
the following tree. Apply
DFS and BFS as studied in
the chapter. Show
the
state of the data structure
Q and the
visited list clearly at
every step. S is the
initial
state and D is the goal
state.
S
A
B
C
D
E
F
G
H
I
72
Artificial
Intelligence (CS607)
Q4 Discuss
how progressive deepening
uses a mixture of DFS and
BFS to
eliminate
the disadvantages of both and at
the same time finds
the solution is a
given
tree. Support your answer
with examples of a few
trees.
Q5 Discuss
the problems in Hill
Climbing. Suggest solutions to
the commonly
encountered
problems that are local
maxima, plateau problem and
ridge problem.
Given
the following tree, use
the hill climbing procedure
to climb up the tree.
Use
your
suggested solutions to the
above mention problems if any of
them are
encountered.
K is the goal state and
numbers written on each node
is the
estimate of
remaining distance to the
goal.
10
S
9
11
A
B
7
9
12
C
D
E
7
7
7
G
H
F
7
5
I
J
0
K
Q6 Discuss
how best first search
works in a tree. Support
your answer with an
example
tree. Is best first search
always the best strategy?
Will it always
guarantee
the best solution?
Q7 Discuss how
beam search with degree of
the search = 3 propagates in
the
given
search tree. Is it equal to
best first search when
the degree = 1.
73
Artificial
Intelligence (CS607)
Q8 Discuss
the main concept behind
branch and bound search
strategy. Suggest
Improvements in
the Algorithm. Simulate the
algorithm on the given graph
below.
The values on
the links are the
distances between the
cities. The numbers on
the
nodes
are the estimated distance
on the node from the
goal state.
Q9.
Run the MiniMax procedure on
the given tree. The static
evaluation scores
for
each leaf node are
written under it. For
example the static
evaluation scores
for
the left most leaf
node is 80.
80
10
55
45
65
100
20
35
70
Q10
Discuss how Alpha Beta
Pruning minimizes the number
of static evaluations
at the
leaf nodes by pruning
branches. Support your
answer with small
examples
of a few
trees.
Q11
Simulate the Minimax
procedure with Alpha Beta
Pruning algorithm on
the
following
search tree.
74
Artificial
Intelligence (CS607)
Maximizing
Level
Minimizing
Level
Maximizing
Level
30
30
50
40
70
60
20
80
90
10
90
70
60
Adapted
from: Artificial Intelligence,
Third Edition by Patrick
Henry Winston
75