PORTFOLIO RISK ANALYSIS AND EFFICIENT PORTFOLIO MAPS

<< 2- STOCK PORTFOLIO THEORY, RISK AND EXPECTED RETURN:Diversification, Definition of Terms

EFFICIENT PORTFOLIOS, MARKET RISK AND CAPITAL MARKET LINE (CML):Market Risk & Portfolio Theory >>

Financial Management MGT201

Lesson 22

PORTFOLIO RISK ANALYSIS AND EFFICIENT PORTFOLIO MAPS

Learning Objectives:

After going through this lecture, you would be able to have an understanding of the following

topics

· Portfolio Risk Analysis & Efficient Portfolio Maps

Before starting the new concepts we should recap what we have studied in the previous lecture.

Recap:

Portfolio is a Collection of Investments in different Stocks, Bonds, other Securities or a mix of

all. Its objective is to invest in Different Un-Correlated Stocks in order to minimize overall Risk &

Maximize Portfolio Return. It is mentioned that individuals and companies maintain the portfolio in

order to reduce to reduce the risk

There are 2 Types of Stock Risk

Total Stock Risk = Diversifiable + Market Risk

Diversification means expanding the number of investments which cover different kinds of

stocks. We can reduce the risk as random events in one industry can be off set by the random effects in

the other industry. This way you can reduce the company pacific or unique risk. The market risk arises

because of micro economic or large scale factors such as market interest rate, inflation etc. These factors

have virtually identical effect on the share prices. For example, in event of a war stick market go down

in value which means almost every share went down.7 Stocks are a good number for diversification. 40

Stocks are enough for Minimizing Total Risk

Calculating Expected 2-Stock Portfolio Return & Risk

Expected Portfolio Return = rP * = xA rA + xB rB

Portfolio Risk is generally not a simple weighted average.

Up to this point we only look at the portfolio which has only two stocks.

Interpreting 2-Stock Portfolio Risk Formula:

= √ XA2 σ A 2 +XB2 σ B 2 + 2 (XA XB σ A σ B

AB)

is coefficient of correlation which states that how muck the investments are correlated.

Here,

The risk of investing in any one share can be reduced if we invest in other shares also. There have been

several experiment studies that show that if you invest in approximately 40 different uncorrelated

different shares of different companies then you can entirely eliminate the company pacific portion of

the risk. Even if you can not diversify across 40 different companies but if you diversify just across 7

different shares from different companies then you can still you can reduce most of the diversifiable risk.

No matter what we do we can not eliminate the market risk that market risk become the minimum risk

we have to live with in our portfolio. The important thing then to remember is that how this risk will

effected when we talk about portfolio of two stocks or more. The Correlation coefficient needs to be

understood in order to understand the risk and return.

Correlation Coefficient (

AB or "Ro"):

Risk of a Portfolio of only 2 Stocks A & B depends on the Correlation between those 2 stocks.

The value of Ro is between -1.0 and +1.0

If Ro = 0 then Investments are Uncorrelated & Risk Formula simplifies to Weighted Average

Formula.

If Ro = + 1.0 then Investments are Perfectly Positively Correlated and this means that

Diversification does not reduce Risk.

If Ro = - 1.0, it means that Investments are Perfectly Negatively Correlated and the Returns (or Prices

or Values) of the 2 Investments move in Exactly Opposite directions. In this Ideal Case, All Risk can be

diversified away. For example, if the price of one stock increases by 50% then the price of another stock

goes down by 50%.

In Reality, Overall Ro for most Stock Markets is about Ro = + 0.6.it is very rough rule of thumb. It

means that correlations are not completely perfect and you should remember that if the correlation

coefficient is +1.0 then it is not possible to reduce the diversifible risk.

This means that increasing the number of Investments in the Portfolio can reduce some amount of risk

but not all risk

Financial Management MGT201

Portfolio Risk - Example Recap

Complete 2-Stock Investment Portfolio Data:

Value (Rs) Exp Return (%) Risk (Std Dev)

Stock A

20%

Stock B

Total Value = 100

Correlation Coeff Ro = + 0.6

2-Stock Portfolio Risk Calculation:

= √ XA2 σ A 2 +XB2 σ B 2 + 2 (XA XB σ A σ B

AB)

= {0.0036 + 0.001225 + 0.00252} 0.5 = 0.0857= 8.57%

· 2-Stock Portfolio Return Calculation:

rP* = x A r A + x B r B = 6 + 7 = 13%

Interpretation of Result:

The Portfolio Risk for our Basket of 2 Investments is

+8.57 % (if Ro = + 0.6). What does this

mean?

Bell Curve Assumption: If we assume a Normal Probability Distribution, then there is a 68.26%

chance that our future Portfolio Return will be somewhere between (rP*- σ ) and (rP*+ σ ) i.e.

between (13% -8.57%) and (13% +8.57%) or between +4.43% and +21.57%

Portfolio Risk lies between the Individual Risks of the 2 Investments i.e

σ Stock B < σ P

σ Stock A or 5% < 8.57% < 20% (if Ro = +0.6)

You can also come up with more accurate outcome about the actual value of the return on the portfolio

after 1 year if you take a larger range for the standard deviation. So, if you are taking about the range

from -2 sigma to +2 sigma towards then there is likelihood that actual rate of return of the portfolio is

somewhere in between the two standard deviation.

Note: If Ro = - 0.6 (Negative Correlation) then Portfolio Risk = + 4.8% which is lower than both

Individual Investments!!

Now, we consider the case of negatively correlated investments.

Negatively Correlated Investments

2-Stock Investment Portfolio Data:

Exp Indiv Return (ri) Indiv Risk (Std Devi )

Stock A 20%

20%

Stock B

10%

Correlation Coeff Ro = - 0.6

Portfolio Risk & Return Table (for Different Portfolio Mixes):

Fraction of Stock A

Portfolio Risk Exp Portfolio Return (rP*)

100%

20% 20%

80%

15% 18% = 0.8(20) + 0.2(10)

50%

15% = 0.5(20) + 0.5(10)

30%

4.8% 13%

15%

3.4% 11.5%

0%(i.e. 100% Stock B) 5%

10%

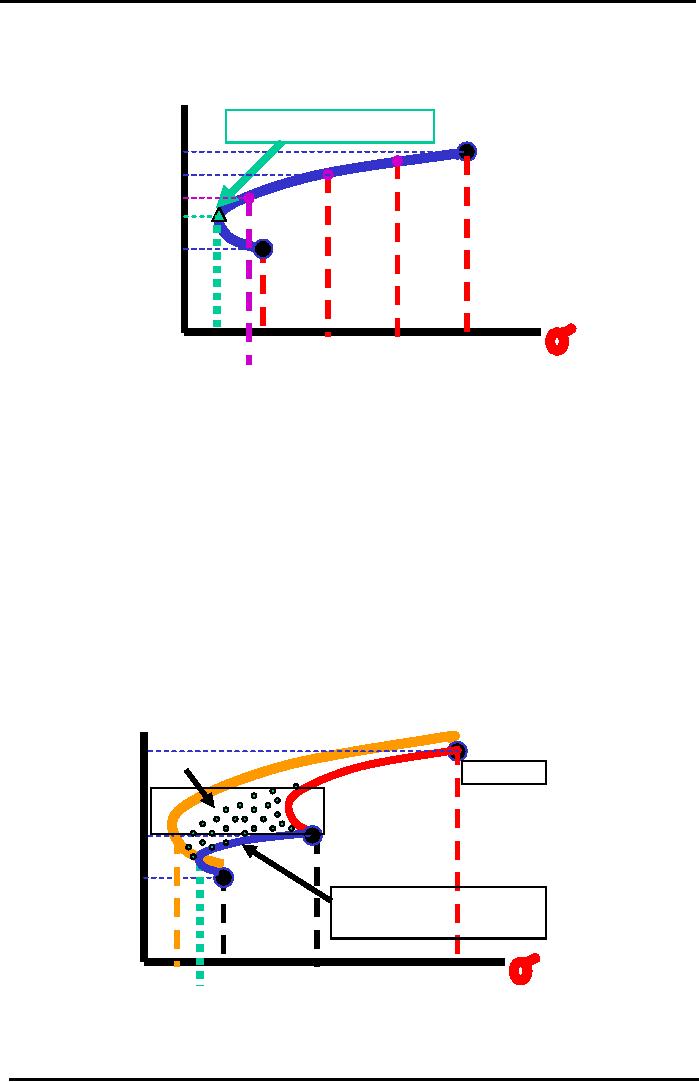
Efficient Portfolio Map

Financial Management MGT201

Efficient Portfolio Map

Shows All Combinations of 2-Stock Portfolio

Negative Correlation (Ro = -0.6)

rP*

Point of Minimum

Portfolio

20%

Risk

Stock A

Return

(100% A &

15%

80%A

50%A

0% B)

13%

30%A

11.5%

15%A

10%

Stock B

(0% A &

100% B)

3.4% 5%

20%

15%

Portfolio Risk

4.8%

Efficient Portfolio Interpretation

Efficient Portfolio Map for 2-Stock Portfolio shows all possible Efficient Combinations (Mixes)

of stocks.

Efficient Portfolios:

Efficient Portfolios are those whose Risk & Return values match the ones computed using

Theoretical Probability Formulas. The Incremental Risk Contribution of a New Stock to a Fully

Diversified Portfolio of 40 Un-Correlated Stocks will be the Market Risk Component of the New Stock

only. The Diversifiable Risk of the New Stock would be entirely offset by random movements in the

other 40 stocks. Adding a New Stock to the existing Portfolio will create more Efficient Portfolio

Curves. The New Stock will contribute its own Incremental Risk and Return to the Portfolio.

rP * = xA rA + xB rB + xC rC (3 Stocks)

Efficient Portfolio Maps

3-Stock Portfolio

Negative Correlation

rP*

Efficient Frontier for

Portfolio 30%

3-Stock Portfolio

Stock C

Return

20%

Stock A

10%

Stock B

Old Efficient Frontier for

2-Stock Portfolio of A & B

40%

2.5% 5%

20%

Portfolio Risk

3.4%

Financial Management MGT201

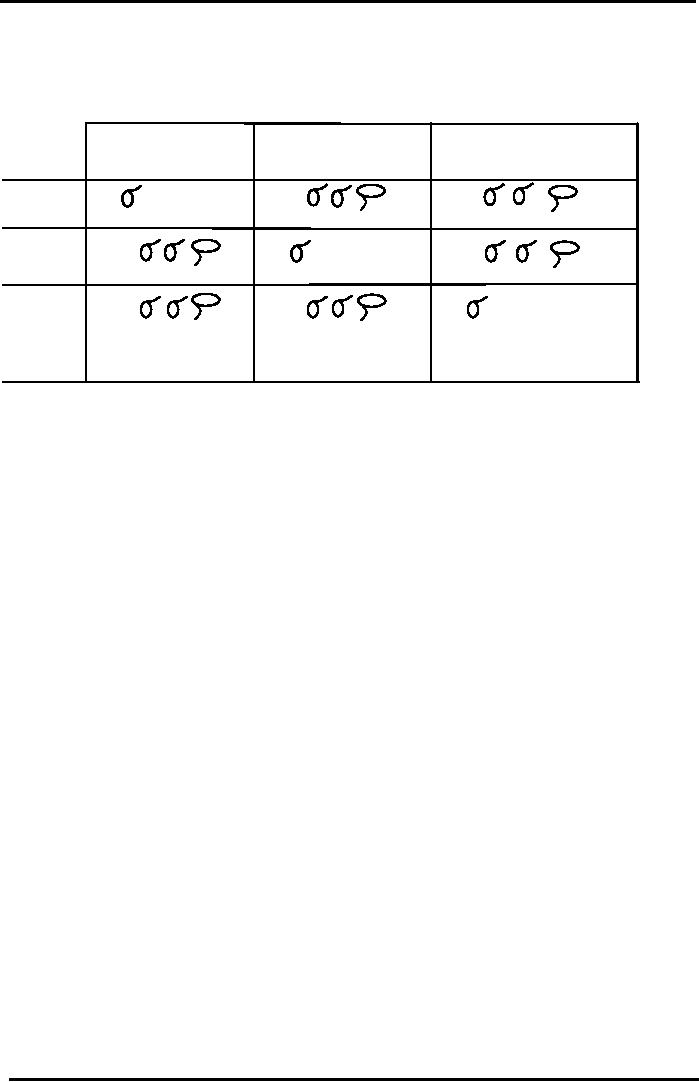
Now, if we add another stock in the portfolio we can take a look

3-Stock Portfolio Risk Formula

3x3 Matrix Approach

Stock A

Stock B

Stock C

XA2

Stock

XA XB

XA XC

XB2

Stock

XB XA

XB XC

XC2

Stock

XC XA

XC XB

To compute the Portfolio Variance for a 3-Stock Portfolio, just add up all the terms in every

box. To compute the Portfolio Risk (Standard Deviation), simply take the Square Root of the Variance.

You can extend this Matrix Approach to calculate the Risk for a Portfolio consisting of any

number of stocks.

Terms in Boxes on Diagonal (Top Left to Bottom Right) are called "VARIANCE" terms associated

with individual magnitude of risk for each stock.

Terms in all other (or NON-DIAGONAL) Boxes are called "COVARIANCE" terms which account for

affect of one stock's movement on another stock's movement.

Table of Contents: