 |

Corporate
Finance FIN 622
VU
Lesson
16
PORTFOLIO
& DIVERSIFICATION
The
following topics will be
discussed in this lecture.
Portfolio
and Diversification
Portfolio
and Variance
Risk
Systematic &
Unsystematic
Beta
Measure of systematic risk
Aggressive
& defensive stocks
Modern
Portfolio Theory (MPT)
proposes how rational
investors will use
diversification to optimize
their
portfolios,
and how an asset should be priced given
its risk relative to the market as a whole.
The basic
concepts
of the theory are Mark with
diversification, the efficient frontier,
capital asset pricing model
and
beta
coefficient, the Capital Market Line and
the Securities Market
Line.
MPT
models the return of an asset as a random
variable and a portfolio as a weighted
combination of
assets;
the return of a portfolio is thus
also a random variable and consequently
has an expected value and
a
variance.
Risk in this model is identified with the
standard deviation of portfolio
return. Rationality is
modeled
by supposing that an investor choosing
between several portfolios
with identical expected
returns
will
prefer that portfolio which
minimizes risk.
Risk
and Reward
The
model assumes that investors
are risk averse. This means
that given two assets that
offer the same
return,
investors will prefer the less risky
one. Thus, an investor will
take on increased risk only
if
compensated
by higher expected returns. Conversely,
an investor who wants higher returns
must accept
more
risk. The exact trade-off
will differ by investor. The
implication is that a rational investor
will not
invest in a
portfolio if a second portfolio
exists with a more favorable
risk-return profile - i.e. if
for that level
of risk an
alternative portfolio exists which
has better expected
returns.
Mean
and Variance
It is
further assumed that
investor's risk / reward preference
can be described via a quadratic
utility
function.
The effect of this assumption is that
only the expected return and
the volatility (i.e. mean
return
and
standard deviation) matter to the
investor. The investor is indifferent to
other characteristics of the
distribution
of returns, such as its
skew. Note that the theory
uses a historical parameter, volatility,
as a
proxy
for risk while return is an expectation
on the future.
Under
the model:
� Portfolio
return is the component-weighted return (the
mean) of the constituent assets.
Return
changes
linearly with component weightings,
wi.
� Portfolio
volatility is a function of the
correlation of the component assets. The
change in volatility
is
non-linear as the weighting of the component
assets changes.
Diversification
An investor
can reduce portfolio risk simply by
holding instruments which
are not perfectly correlated.
In
other
words, investors can reduce
their exposure to individual
asset risk by holding a diversified
portfolio of
assets.
Diversification will allow
for the same portfolio
return with reduced risk.
For diversification to
work
the component
assets must not be perfectly
correlated, i.e. correlation
coefficient not equal to
1.
Capital
Allocation Line
The
Capital
Allocation Line (CAL) is the
line that connects all
portfolios that can be
formed using a risky
asset
and a risk-less asset. It
can be proven that it is a straight
line and that it has the
following equation.
In this
formula P is the risky portfolio, F is the
risk-less portfolio and C is a
combination of portfolios P
and
F.
The
Efficient Frontier
Every
possible asset combination
can be plotted in risk-return
space, and the collection of
all such possible
portfolios
defines a region in this space. The
line along the upper edge of this region is
known as the
efficient
frontier (sometimes "the
Mark witz"). Combinations along this line
represent portfolios for
which
there
is lowest risk for a given level of
return. Conversely, for a given amount of
risk, the portfolio lying
on
the
efficient frontier represents the
combination offering the best
possible return. Mathematically
the
50

Corporate
Finance FIN 622
VU
Efficient
Frontier is the intersection
of the Set of Portfolios with
Minimum Variance and the Set
of
Portfolios
with Maximum Return.
The
efficient frontier will be
concave this is because the
risk-return characteristics of a
portfolio change in
a
non-linear fashion as its component
weightings are changed. (As
described above, portfolio risk is
a
function
of the correlation of the component assets,
and thus changes in a
non-linear fashion as the
weighting of
component assets changes.)
The
region above the frontier is unachievable
by holding risky assets alone. No
portfolios can be
constructed
corresponding to the points in this region. Points
below the frontier are suboptimal. A
rational
investor
will hold a portfolio only
on the frontier.
The Risk-Free
Asset
The
risk-free asset is the (hypothetical) asset
which pays a risk-free rate - it is
usually provied by an
investment in
short-dated Government bonds. The
risk-free asset has zero
variance in returns (hence
is
risk-free); it is
also uncorrelated with any
other asset (by definition:
since its variance is zero).
As a result,
when
it is combined with any other
asset, or portfolio of assets, the
change in return and also in
risk is
linear.
Because
both risk and return change
linearly as the risk-free asset is
introduced into a portfolio,
this
combination
will plot a straight line in risk
return space. The line
starts at 100% in cash and weight of
the
risky
portfolio = 0 (i.e. intercepting the
return axis at the risk-free rate)
and goes through the
portfolio in
question
where cash holding = 0 and
portfolio weight = 1.
Portfolio
Leverage
An investor
can add leverage to the
portfolio by holding the risk-free asset.
The addition of the risk-free
asset
allows for a position in the region
above the efficient frontier.
Thus, by combining a risk-free
asset
with
risky assets, it is possible to construct
portfolios whose risk-return
profiles are superior to those on
the
efficient
frontier.
� An investor
holding a portfolio of risky assets,
with a holding in cash, has
a positive risk-free
weighting
(a de-leveraged portfolio). The
return and standard
deviation will be lower than
the
portfolio
alone, but since the
efficient frontier is convex, this
combination will sit above
the
efficient
frontier i.e. offering a higher
return for the same risk as the
point below it on the
frontier.
� The
investor who borrows money to fund
his/her purchase of the risky assets
has a negative risk-
free
weighting -i.e. a leveraged
portfolio. Here the return is
geared to the risky portfolio.
This
combination
will again offer a return
superior to those on the frontier.
The
Market Portfolio
The
efficient frontier is a collection of
portfolios, each one optimal
for a given amount of risk. A
quantity
known
as the Sharp ratio represents a
measure of the amount of additional
return (above the risk-free
rate)
a
portfolio provides compared to the risk it
carries. The portfolio on the
efficient frontier with the
highest
Sharpe
Ratio is known as the market portfolio,
or sometimes the super-efficient portfolio. This
portfolio
has
the property that any
combination of it and the risk-free asset
will produce a return that
is above the
efficient
frontier - offering a larger
return for a given amount of risk than a
portfolio of risky assets on the
frontier
would.
Capital
Market Line
When
the market portfolio is combined with the
risk-free asset, the result is the Capital
Market Line. All
points
along the CML have superior risk-return
profiles to any portfolio on the
efficient frontier. (A
position
with zero cash weighting is
on the efficient frontier - the market
portfolio.)
The
CML is illustrated above, with
return μp on the y
axis, and risk σp on the x
axis.
One
can prove that the CML is
the optimal CAL and that
its equation is:
Asset
Pricing
A
rational investor would not invest in an
asset which does not
improve the risk-return characteristics
of his
existing
portfolio. Since a rational investor
would hold the market
portfolio, the asset in question will
be
added
to the market portfolio. MPT
derives the required return for a
correctly priced asset in this context.
51
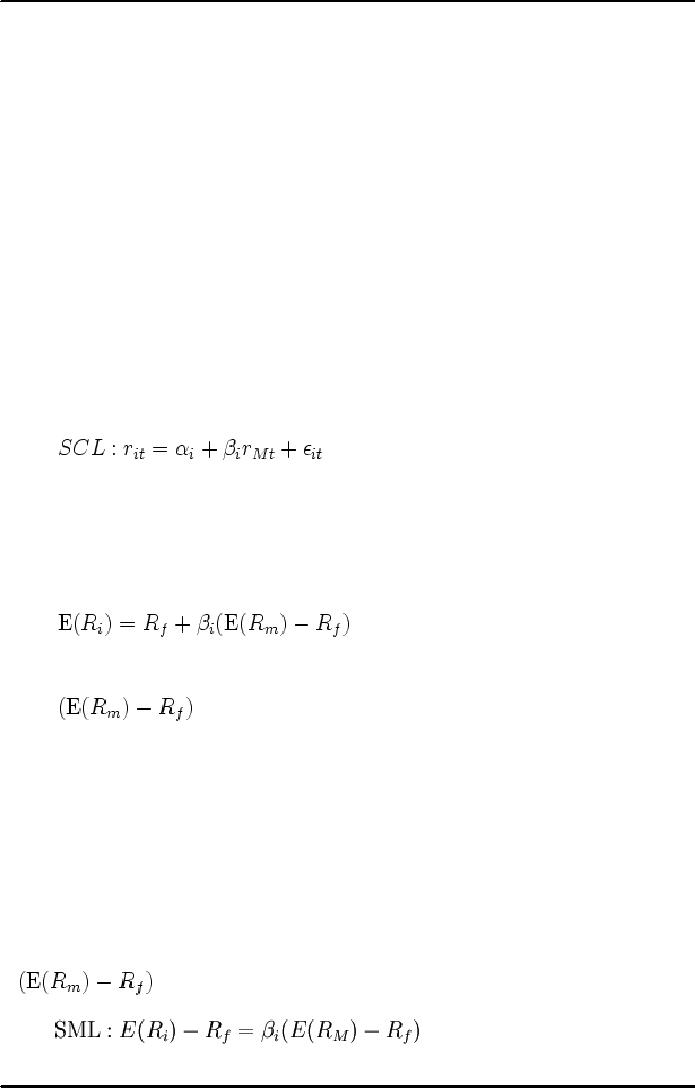
Corporate
Finance FIN 622
VU
Systematic
Risk and Specific
Risk
Specific
risk is the risk associated with
individual assets - within a
portfolio these risks can be
reduced
through
diversification (specific risks
"cancel out"). Systematic risk, or
market risk, refers to the risk
common to
all securities - except for
selling short as noted below, systematic
risk cannot be diversified away
(within
one market). Within the
market portfolio, asset
specific risk will be diversified
away to the extent
possible.
Systematic risk is therefore equated with
the risk (standard deviation) of the
market portfolio.
Since
a security will be purchased
only if it improves the risk / return
characteristics of the market
portfolio,
the risk of a
security will be the risk it adds to the
market portfolio. In this context, the
volatility of the asset,
and
its correlation with the
market portfolio, is historically
observed and is therefore a given (there
are
several
approaches to asset pricing
that attempt to price assets by modeling
the stochastic properties of the
moments
of assets' returns - these
are broadly referred to as conditional
asset pricing models).
The
(maximum)
price paid for any particular
asset (and hence the return
it will generate) should also
be
determined
based on its relationship with the
market portfolio.
Systematic
risks within one market
can be managed through a
strategy of using both long
and short
positions
within one portfolio,
creating a "market neutral"
portfolio.
Security
Characteristic Line
The
Security
Characteristic Line (SCL)
represents the relationship between the
market
return (rM) and
the
return of a given asset i (ri) at a given time t. In general, it is
reasonable to assume that the
SCL is a
straight
line and can be illustrated as a
statistical equation:
where
αi is called the
asset's alpha coefficient
and βi the asset's beta
coefficient.
Capital
asset pricing
model
The
asset return depends on the amount paid
for the asset today. The
price paid must ensure that
the
market
portfolio's risk / return characteristics
improve when the asset is
added to it. The CAPM is a
model
which
derives the theoretical required return
(i.e. discount rate) for an
asset in a market, given the
risk-free
rate
available to investors and the risk of
the market as a whole.
The
CAPM is usually
expressed:
�
β,
Beta, is the measure of asset sensitivity
to a movement in the overall market; Beta
is usually
found
via regression on historical data. Betas
exceeding one signify more
than average "risk
ness";
betas
below one indicate lower than
average.
�
is the
market premium, the historically observed
excess return of the
market
over
the risk-free rate'
Once
the expected return, E(ri), is calculated using CAPM,
the future cash flows of the
asset can be
discounted
to their present value using
this rate to establish the correct
price for the asset. (Here
again, the
theory
accepts in its assumptions
that a parameter based on
past data can be combined
with a future
expectation.)
A more
risky stock will have a higher
beta and will be discounted
at a higher rate; less sensitive
stocks will
have
lower betas and be
discounted at a lower rate. In theory, an
asset is correctly priced when its
observed
price
is the same as its value
calculated using the CAPM derived
discount rate. If the observed price
is
higher
than the valuation, then the
asset is overvalued; it is undervalued for a
too low price.
Securities
Market Line
The
relationship between Beta & required
return is plotted on the securities
market line (SML) which
shows
expected
return as a function of β. The
intercept is the risk-free rate available
for the market, while the
slope
is
. The
Securities market line can
be regarded as representing a single-factor model
of
the
asset price, where Beta is
exposure to changes in value of the
Market. The equation of the SML is
thus:
52

Corporate
Finance FIN 622
VU
Comparison
with Arbitrage Pricing Theory
The
SML and CAPM are
often contrasted with the
Arbitrage pricing theory
(APT), which holds that
the
expected
return of a financial asset
can be modeled as a linear function of
various macro-economic
factors,
where
sensitivity to changes in each factor is
represented by a factor specific
bets coefficient.
The
APT is less restrictive in its
assumptions: it allows for an explanatory
(as opposed to statistical)
model
of
asset returns, and assumes
that each investor will hold
a unique portfolio with its
own particular array of
betas,
as opposed to the identical "market
portfolio". Unlike the CAPM, the
APT, however, does not
itself
reveal
the identity of its priced factors - the
number and nature of these
factors is likely to change
over time
and
between economies.
53
Table of Contents:
- INTRODUCTION TO SUBJECT
- COMPARISON OF FINANCIAL STATEMENTS
- TIME VALUE OF MONEY
- Discounted Cash Flow, Effective Annual Interest Bond Valuation - introduction
- Features of Bond, Coupon Interest, Face value, Coupon rate, Duration or maturity date
- TERM STRUCTURE OF INTEREST RATES
- COMMON STOCK VALUATION
- Capital Budgeting Definition and Process
- METHODS OF PROJECT EVALUATIONS, Net present value, Weighted Average Cost of Capital
- METHODS OF PROJECT EVALUATIONS 2
- METHODS OF PROJECT EVALUATIONS 3
- ADVANCE EVALUATION METHODS: Sensitivity analysis, Profitability analysis, Break even accounting, Break even - economic
- Economic Break Even, Operating Leverage, Capital Rationing, Hard & Soft Rationing, Single & Multi Period Rationing
- Single period, Multi-period capital rationing, Linear programming
- Risk and Uncertainty, Measuring risk, Variability of return–Historical Return, Variance of return, Standard Deviation
- Portfolio and Diversification, Portfolio and Variance, Risk–Systematic & Unsystematic, Beta – Measure of systematic risk, Aggressive & defensive stocks
- Security Market Line, Capital Asset Pricing Model – CAPM Calculating Over, Under valued stocks
- Cost of Capital & Capital Structure, Components of Capital, Cost of Equity, Estimating g or growth rate, Dividend growth model, Cost of Debt, Bonds, Cost of Preferred Stocks
- Venture Capital, Cost of Debt & Bond, Weighted average cost of debt, Tax and cost of debt, Cost of Loans & Leases, Overall cost of capital – WACC, WACC & Capital Budgeting
- When to use WACC, Pure Play, Capital Structure and Financial Leverage
- Home made leverage, Modigliani & Miller Model, How WACC remains constant, Business & Financial Risk, M & M model with taxes
- Problems associated with high gearing, Bankruptcy costs, Optimal capital structure, Dividend policy
- Dividend and value of firm, Dividend relevance, Residual dividend policy, Financial planning process and control
- Budgeting process, Purpose, functions of budgets, Cash budgets–Preparation & interpretation
- Cash flow statement Direct method Indirect method, Working capital management, Cash and operating cycle
- Working capital management, Risk, Profitability and Liquidity - Working capital policies, Conservative, Aggressive, Moderate
- Classification of working capital, Current Assets Financing – Hedging approach, Short term Vs long term financing
- Overtrading – Indications & remedies, Cash management, Motives for Cash holding, Cash flow problems and remedies, Investing surplus cash
- Miller-Orr Model of cash management, Inventory management, Inventory costs, Economic order quantity, Reorder level, Discounts and EOQ
- Inventory cost – Stock out cost, Economic Order Point, Just in time (JIT), Debtors Management, Credit Control Policy
- Cash discounts, Cost of discount, Shortening average collection period, Credit instrument, Analyzing credit policy, Revenue effect, Cost effect, Cost of debt o Probability of default
- Effects of discounts–Not effecting volume, Extension of credit, Factoring, Management of creditors, Mergers & Acquisitions
- Synergies, Types of mergers, Why mergers fail, Merger process, Acquisition consideration
- Acquisition Consideration, Valuation of shares
- Assets Based Share Valuations, Hybrid Valuation methods, Procedure for public, private takeover
- Corporate Restructuring, Divestment, Purpose of divestment, Buyouts, Types of buyouts, Financial distress
- Sources of financial distress, Effects of financial distress, Reorganization
- Currency Risks, Transaction exposure, Translation exposure, Economic exposure
- Future payment situation – hedging, Currency futures – features, CF – future payment in FCY
- CF–future receipt in FCY, Forward contract vs. currency futures, Interest rate risk, Hedging against interest rate, Forward rate agreements, Decision rule
- Interest rate future, Prices in futures, Hedging–short term interest rate (STIR), Scenario–Borrowing in ST and risk of rising interest, Scenario–deposit and risk of lowering interest rates on deposits, Options and Swaps, Features of opti
- FOREIGN EXCHANGE MARKET’S OPTIONS
- Calculating financial benefit–Interest rate Option, Interest rate caps and floor, Swaps, Interest rate swaps, Currency swaps
- Exchange rate determination, Purchasing power parity theory, PPP model, International fisher effect, Exchange rate system, Fixed, Floating
- FOREIGN INVESTMENT: Motives, International operations, Export, Branch, Subsidiary, Joint venture, Licensing agreements, Political risk