 |
PDA corresponding to CFG |
| << Nondeterministic PDA |
| Conversion form of PDA >> |

Theory of
Automata
(CS402)
Theory of
Automata
Lecture
N0. 39
Reading
Material
Introduction
to Computer Theory
Chapter
15
Summary
PDA
corresponding to CFG, Examples of PDA corresponding to
CFG
PDA
corresponding to CFG
Theorem
Corresponding to
any CFG there exists a
PDA accepting the language
generated by the CFG.
Since an
algorithm has already been
discussed to convert the CFG
in CNF, so the PDA can be
constructed
corresponding to
the CFG. As the CFG in CNF
generates all the nonnull
words of the corresponding CFL,
so
accepting
the null string (if it is
contained in the CFL), can
be managed separately.
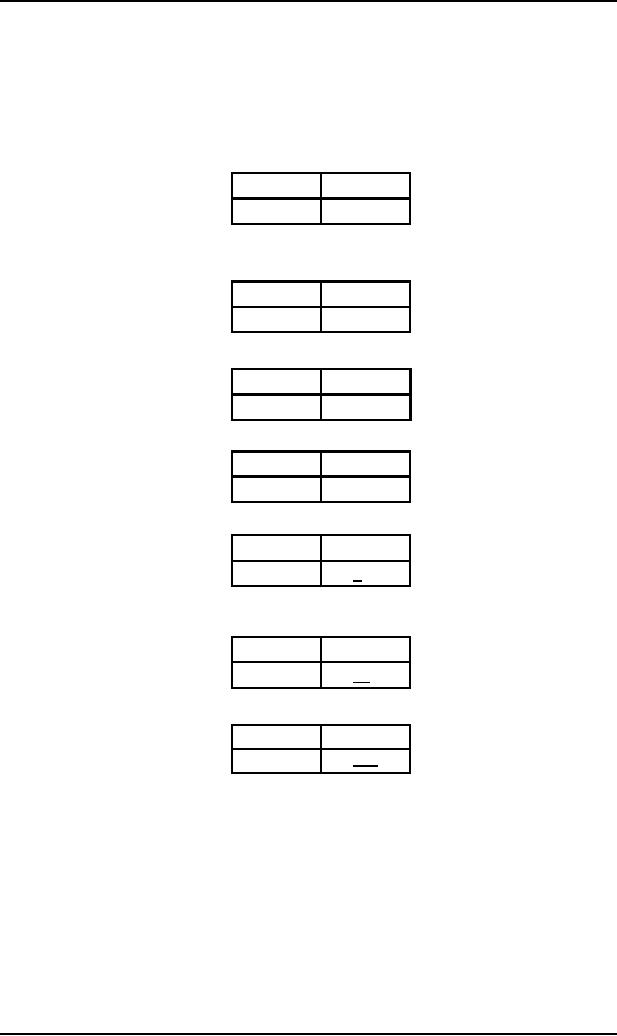
Example
Consider
the following CFG which is
in CNF and does not generate
the null string
S ∆ SB|AB
A ∆ CC
B∆b
C∆a
The
corresponding PDA will be
a
b
READ1
READ2
ACCEPT
START
C
B
READ3
PUSH
S
POP
S
A
S
PUSH
C
PUSH
B
PUSH
B
PUSH
S
PUSH
A
PUSH
C
Here the
STACK alphabet G= {S, A,
B, C}, where the TAPE
alphabet ¬={a,
b}
Note: It
may be noted that when
the POP state is entered
either a nonterminal is replaced by two
nonterminals at
the top
of the STACK accommodating a production,
or a nonterminal is popped out from the
top of the stack
and a
READ state is entered to
read a specified letter from the
TAPE or else the machine
crashes.
The
choice of path taken at POP
state to accommodate the
word belonging to the CFL
can be determined by the
left
most derivation of the word.
Consider the word aab with
its left most derivation, as
follows
119
Theory of
Automata
(CS402)
Working-String
Generation
Production
Used
S fi AB
S ∆ AB
step
1
fi CCB
A ∆ CC
step
2
fi aCB
C∆a
step
3
fi aaB
C∆a
step
4
fi aab
B∆b
step
5
First of
all the START state is
entered
STACK
TAPE
...
aab
...
The PUSH
S state is entered
STACK
TAPE
aab ...
S
The
POP state is entered and to
accommodate the production S ∆ AB, PUSH
B and PUSH A states are
entered.
STACK
TAPE
aab ...
AB
Then
the POP state is entered
and to accommodate the
production A ∆ CC, PUSH
C, PUSH C states are
entered
STACK
TAPE
CCB
aab
The
POP state is entered and to
accommodate the production C ∆ a,
READ1 is entered and
the letter a is read
from
the TAPE.
STACK
TAPE
CB
aab
The
POP state is entered and to
accommodate the production C ∆ a,
READ1 state is entered
and the letter a is
read
from the TAPE
STACK
TAPE
aab
B
The
POP state is entered and to
accommodate the production B ∆ b,
READ2 state is entered
and the letter b is
read
from the TAPE
STACK
TAPE
aab
D
The
D
shown in
the STACK indicates that
there are no nonterminals in the
working string and D is read
from the
STACK
which leads to READ3 state where the D is read
from the TAPE and
the ACCEPT state is
entered
which
shows that the word
aab is accepted by the
PDA.
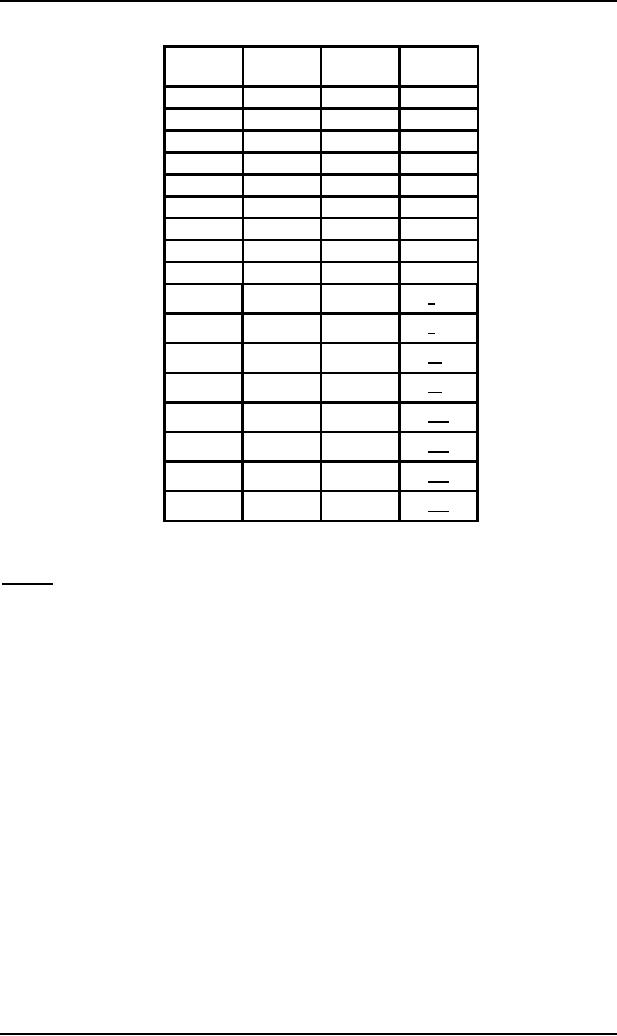
Following
is the table showing all
the observations discussed above, for
the word aab
120
Theory of
Automata
(CS402)
Left
most
STATE
STACK
TAPE
derivation
D
START
aab
S
PUSH
S
S
aab
D
POP
aab
aab
PUSH
B
B
fiAB
PUSH
A
AB
aab
POP
B
aab
PUSH
C
CB
aab
fiCCB
PUSH
C
CCB
aab
POP
CB
aab
fiaCB
READ1
CB
aab
POP
B
aab
fiaaB
READ1
B
aab
D
POP
aab
fiaab
D
READ2
aab
D
POP
aab
D
READ3
aab
D
ACCEPT
aab
Following
is an example of building the
PDA corresponding to the given
CFG
Example
Consider
the following CFG
S ∆ XY
X ∆ aX | bX
|a
Y ∆ Ya | Yb |
a
First of
all, converting the CFG to
be in CNF, introduce the nonterminals A
and B as
A∆a
B∆b
The
following CFG is in
CNF
S ∆ XY
X ∆ AX | BX
|a
Y ∆ YA | YB |
a
A∆a
B∆b
121
Theory of
Automata
(CS402)
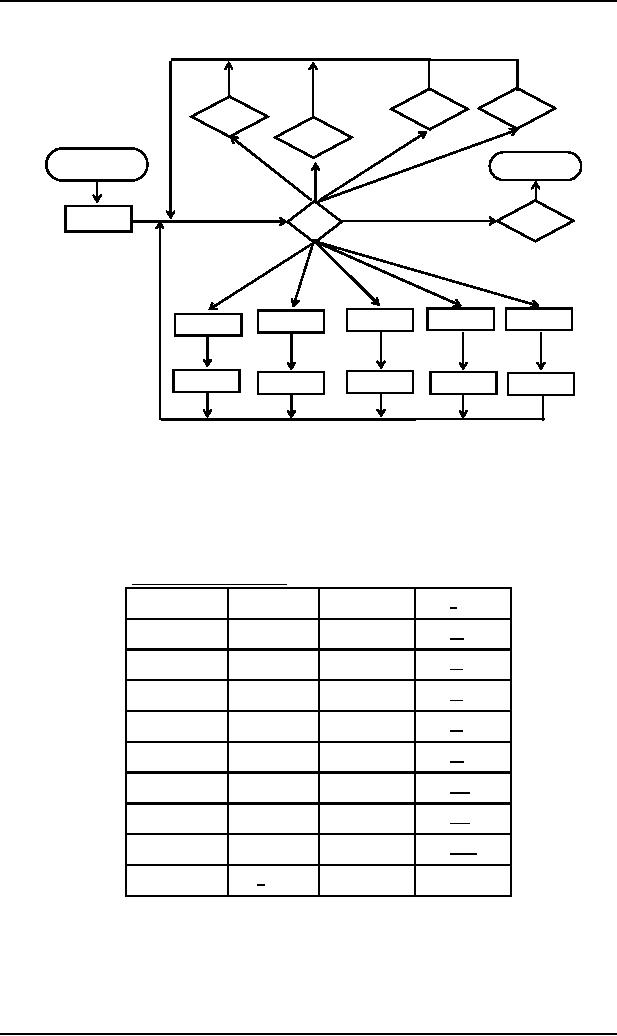
The
PDA corresponding to the above
CFG will be
a
b
a
a
READ3
READ4
READ1
READ2
B
A
START
ACCEPT
Y
X
PUSH
S
READ5
POP
S
Y
X
X
Y
PUSH
B
PUSH
X
PUSH
A
PUSH
X
PUSH
Y
PUSH
X
PUSH
B
PUSH
A
PUSH
Y
PUSH
Y
The
word aaab can be generated
as
Working-String
Generation
Production
Used
S fi XY
S ∆ XY
step
1
fi AXY
X ∆ AX
step
2
fi aXY
A∆a
step
3
fi aaY
X∆a
step
4
fi aaYB
Y ∆ YB
step
5
fi aaaB
Y∆a
step
6
fi aaab
B∆b
step
7
STACK
TAPE
STACK
TAPE
(START)
aaab
(POP)
Y
aaab
(PUSH S)
S
aaab
(READ1) Y
aaab
(POP)
(POP)
aaab
aabb
(PUSH Y)
Y
aaab
(PUSH B)
B
aabb
(PUSH X)
XY
aaab
(PUSH Y)
YB
aabb
aaab
(POP)
Y
aaab
(POP)
B
(PUSH X)
XY
aaab
(READ2) B
aaab
(POP)
(PUSH A)
AXY
aaab
aaab
(POP)
XY
aaab
(READ4)
aaab
(POP)
(READ3) XY
aaab
122
Table of Contents:
- What does automata mean, Introduction to languages
- Kleene Star Closure, Recursive definition of languages
- Regular Expression, Recursive definition of Regular Expression
- Equivalent Regular Expressions
- Finite Automaton
- Equivalent FAs
- FA corresponding to finite languages
- Examples of TGs: accepting all strings
- Generalized Transition Graphs
- Nondeterminism, Kleeneís Theorem
- Proof(Kleeneís Theorem Part II)
- Kleeneís Theorem Part III
- Concatenation of FAs
- Closure of an FA
- Nondeterministic Finite Automaton, Converting an FA to an equivalent NFA
- NFA with Null String
- NFA and Kleeneís Theorem
- NFA corresponding to Concatenation of FAs
- Distinguishable strings and Indistinguishable strings
- Finite Automaton with output, Moore machine
- Mealy machine
- Equivalent machines
- Mealy machines in terms of sequential circuit
- Regular languages, Complement of a language
- Nonregular languages
- Pumping Lemma
- Pumping Lemma version II
- Pseudo theorem
- Decidability
- finiteness of a language
- Context Free Grammar (CFG), CFG terminologies
- Trees
- Polish Notation (o-o-o)
- Total language tree, Regular Grammar
- Null Production
- Chomsky Normal Form (CNF)
- A new format for FAs
- Nondeterministic PDA
- PDA corresponding to CFG
- Conversion form of PDA
- Conversion Form, Joints of the machine
- Row language, Nonterminals
- Non-Context-Free language, Pumping lemma for CFLs
- Decidablity, Parsing Techniques
- Turing machine