 |
Advanced Computer
Architecture-CS501
________________________________________________________
Advanced
Computer Architecture
Lecture
No. 35
Reading
Material
Vincent
P. Heuring & Harry F. Jordan
Chapter
6
Computer
Systems Design and Architecture
6.3,
6.4
Summary
·
Overflow
·
Different
Implementations of the
adder
·
Unsigned
and Signed Multiplication
·
Integer
and Fraction Division
·
Branch
Architecture
Overflow
When
two m-bit numbers are
added and the result exceeds
the capacity of an
m-bit
destination,
this situation is called an
overflow. The following
example describes
this
condition:
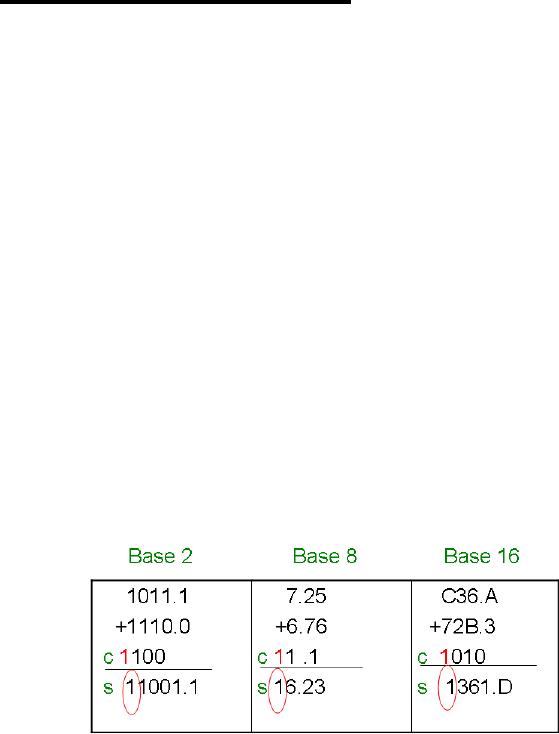
Example
1
Overflow
in fixed point
addition:
In these
three cases, the fifth
position is not allowed so
this results in an
overflow.
Different
Implementations of the Adder
For a
binary adder, the sum bit is
obtained by following
equation:
__ _ _
__
sj = xjyjcj+xjyjcj+xjyjcj+xjyjcj
and the
equation for carry bit
is
cj+1=xjyj+xjcj+yjcj
where x
and y are the input
bits.
Page
334
Last
Modified: 01-Nov-06
Advanced Computer
Architecture-CS501
________________________________________________________
The
sum can be computed by the
two methods:
·
Ripple
Carry Adder
·
Carry
Look ahead Adder
Ripple
Carry Adder
In this
adder circuit, we feed carry
out from the previous
stage to the next stage and
so
on.
For 64 bit addition, 126
logic levels are required
between the input and output
bits.
The
logic levels can be reduced by using a
higher base (Base 16).
This is a relatively
slow
process.
Complement
Adder/Subtractor
We can
perform subtraction using an
unsigned adder by
·
Complement the second
input
·
Supply overflow detection
hardware
2's
Complement Adder/Subtractor
A
combined adder/subtractor can be built
using a mux to select the
second adder input.
In
this
case, the mux also
determines the carry-in to
the adder. The equation for
mux output
is
:
_ _
qj =y j r + yj r
Carry
Look ahead Adder
The
basic idea in carry look
ahead is to speed up the
ripple carry by determining
whether
the
carry is generated at the j
position after addition,
regardless of the carry-in at
that
stage or
the carry is propagated from
input to output in the
digit.
This
results in faster addition and
lesser propagation delay of
the carry bits. It divides
the
carry
into two logical variables
Gj (generate) and Pj (propagate). These variables
are
defined
as:
Gj = xjyj
P j = x j
+y j
Hence
the carry out will be
c j +1= G j
+P j c j
Here
the G and P each require one
gate, and the sum bit
needs two more gates in
the full
adder.
This results in a less
complexity i.e. log(m) which
is much less as compare to
ripple
carry adder where complexity
is m (m is the number of bits of a
digit to be added).
Ripple
carry and look ahead schemes
are can be mixed by producing a
carry-out at the
left end
of each look ahead module
and using ripple carry to
connect modules at any
level
of the
look ahead tree.
Unsigned
Multiplication
The
general schema for unsigned
multiplication in base b is shown in
Figure 6.5 of the
text
book.
Page
335
Last
Modified: 01-Nov-06
Advanced Computer
Architecture-CS501
________________________________________________________
Parallel
Array Multiplier
Figure
6.6 of the text book
shows the structure of a fully
parallel array multiplier
for base
b
integers. All signal lines
carry base b digits and each
computational block consists of a
full
adder with an AND gate to
form the product xiyj. In case of
binary, m2
full adders
are
required
and the signals will have to
pass through almost 4m
gates.
Series
parallel Multiplier
A
combination of parallel and sequential
hardware is used to build a
multiplier. This
results
in a good speed of operation and also
saves the hardware.
Signed
Multiplication
The
sign of a product is easily
computed from the sign of
the multiplier and
the
multiplicand.
The product will be positive if
both have same sign and
negative if both
have
different sign. Also, when
two unsigned digits having m
and n bits respectively
are
multiplied,
this results in a (m+n)
bit product, and (m+n+1)-bit
product in case of
sign
digits.
There are three methods
for the multiplication of
sign digits:
1. 2's
complement multiplier
2. Booth
recoding
3.
Bit-Pair recoding
2's complement
Multiplication
If
numbers are represented in 2's
complement form then the
following three
modifications
are required:
1.
Provision for sign
extension
2.
Overflow prevention
3.
Subtraction as well as addition of
the partial product
Booth
Recoding
The
Booth Algorithm makes
multiplication simple to implement at
hardware level and
speed up
the procedure. This
procedure is as follows:
1. Start
with LSB and for each 0 of
the original number, place a 0 in
the recorded
number
until a 1 in indicated.
2. Place
a 1 for 1in the recorded
table and skip any succeeding
1's until a 0 is
encountered.
3. Place
a 0 with 1 and repeat the
procedure.
Example
2
Recode
the integer 485 according to
Booth procedure.
Page
336
Last
Modified: 01-Nov-06
Advanced Computer
Architecture-CS501
________________________________________________________
Solution
Original
number:
00111100101=256+128+64+32+4+1=485
Recoded
Number:
_
_ _
01000101111=+512-32+8-4+2-1=485
Bit-Pair
Recoding
Booth
recoding may increase the
number of additions due to the
number of isolated
1s.
To avoid
this, bit-pair recoding is
used. In bit-pair recoding,
bits are encoded in pairs
so
there
are only n/2 additions
instead of n.
Division
There
are two types of
division:
·
Integer
division
·
Fraction
division
Integer
division
The
following steps are used
for integer division:
1. Clear
upper half of dividend
register and put dividend in
lower half.
Initialize
quotient
counter bit to 0
2. Shift
dividend register left 1
bit
3. If
difference is +ve, put it
into upper half of dividend
and shift 1 into quotient.
If
ve,
shift 0 into quotient
4. If
quotient bits<m, goto
step 2
5. m-bit
quotient is in quotient register and
m-bit remainder is in upper
half of
dividend
register
Example
3
Divide
4710 by 510.
Solution
D=000000
101111,
d=000101
D
000001
011110
d
000101
Diff(-)
q
0
D
000010
111100
Page
337
Last
Modified: 01-Nov-06
Advanced Computer
Architecture-CS501
________________________________________________________
d
000101
Diff(-)
q
00
D
000101
111000
d
000101
Diff(+)
q
001
D
000001
110000
d
000101
Diff(-)
q
0010
D
000011
100000
d
000101
Diff(-)
q
00100
D
000111
000000
d
000101
Diff(+)000010
q
001001
Hence
remainder = (000010)2 = 210
Quotient
= (001001)2
= 910
Fraction
Division
The
following steps are used
for fractional
division:
1. Clear
lower half of dividend
register and put dividend in
upper half.
Initialize
quotient
counter bit to 0
2. If
difference is +ve, report
overflow
3. Shift
dividend register left 1
bit
4. If
difference is +ve, put it
into upper half of dividend
and shift 1 into quotient.
If
negative,
shift 0 into quotient
5. If
quotient bits<m, go to step
3
6. m-bit
quotient has decimal at the
left end and remainder is in upper
half of
dividend
register
Branch
Architecture
The
next important function
perform by the ALU is branch.
Branch architecture of a
machine
is based on
1.
condition codes
2.
conditional branches
Condition
Codes
Condition
Codes are computed by the
ALU and stored in processor status register.
The
`comparison'
and `branching' are treated as two
separate operations. This approach is
not
used in
the SRC. Table 6.6 of
the text book shows
the condition codes after
subtraction,
for
signed and unsigned x and y. Also see
the SRC Approach from text
book.
Page
338
Last
Modified: 01-Nov-06
Advanced Computer
Architecture-CS501
________________________________________________________
Usually
implementation with flags is
easier however it requires status
registers. In case of
branch
instructions, decision is based on
the branch itself.
Note:
For more information on this
topic, please see chapter 6
of the text book.
Page
339
Last
Modified: 01-Nov-06
Table of Contents:
- Computer Architecture, Organization and Design
- Foundations of Computer Architecture, RISC and CISC
- Measures of Performance SRC Features and Instruction Formats
- ISA, Instruction Formats, Coding and Hand Assembly
- Reverse Assembly, SRC in the form of RTL
- RTL to Describe the SRC, Register Transfer using Digital Logic Circuits
- Thinking Process for ISA Design
- Introduction to the ISA of the FALCON-A and Examples
- Behavioral Register Transfer Language for FALCON-A, The EAGLE
- The FALCON-E, Instruction Set Architecture Comparison
- CISC microprocessor:The Motorola MC68000, RISC Architecture:The SPARC
- Design Process, Uni-Bus implementation for the SRC, Structural RTL for the SRC instructions
- Structural RTL Description of the SRC and FALCON-A
- External FALCON-A CPU Interface
- Logic Design for the Uni-bus SRC, Control Signals Generation in SRC
- Control Unit, 2-Bus Implementation of the SRC Data Path
- 3-bus implementation for the SRC, Machine Exceptions, Reset
- SRC Exception Processing Mechanism, Pipelining, Pipeline Design
- Adapting SRC instructions for Pipelined, Control Signals
- SRC, RTL, Data Dependence Distance, Forwarding, Compiler Solution to Hazards
- Data Forwarding Hardware, Superscalar, VLIW Architecture
- Microprogramming, General Microcoded Controller, Horizontal and Vertical Schemes
- I/O Subsystems, Components, Memory Mapped vs Isolated, Serial and Parallel Transfers
- Designing Parallel Input Output Ports, SAD, NUXI, Address Decoder , Delay Interval
- Designing a Parallel Input Port, Memory Mapped Input Output Ports, wrap around, Data Bus Multiplexing
- Programmed Input Output for FALCON-A and SRC
- Programmed Input Output Driver for SRC, Input Output
- Comparison of Interrupt driven Input Output and Polling
- Preparing source files for FALSIM, FALCON-A assembly language techniques
- Nested Interrupts, Interrupt Mask, DMA
- Direct Memory Access - DMA
- Semiconductor Memory vs Hard Disk, Mechanical Delays and Flash Memory
- Hard Drive Technologies
- Arithmetic Logic Shift Unit - ALSU, Radix Conversion, Fixed Point Numbers
- Overflow, Implementations of the adder, Unsigned and Signed Multiplication
- NxN Crossbar Design for Barrel Rotator, IEEE Floating-Point, Addition, Subtraction, Multiplication, Division
- CPU to Memory Interface, Static RAM, One two Dimensional Memory Cells, Matrix and Tree Decoders
- Memory Modules, Read Only Memory, ROM, Cache
- Cache Organization and Functions, Cache Controller Logic, Cache Strategies
- Virtual Memory Organization
- DRAM, Pipelining, Pre-charging and Parallelism, Hit Rate and Miss Rate, Access Time, Cache
- Performance of I/O Subsystems, Server Utilization, Asynchronous I/O and operating system
- Difference between distributed computing and computer networks
- Physical Media, Shared Medium, Switched Medium, Network Topologies, Seven-layer OSI Model