 |
Null Production |
| << Total language tree, Regular Grammar |
| Chomsky Normal Form (CNF) >> |
Theory of
Automata
(CS402)
Theory of
Automata
Lecture
N0. 35
Reading
Material
Introduction
to Computer Theory
Chapter
13
Summary
Examples
of building TG's corresponding to the
Regular Grammar, Null productions with
examples, Nullable
productions
with examples, Unit
production with example,
Chomsky Normal Form
(Definition)
Example
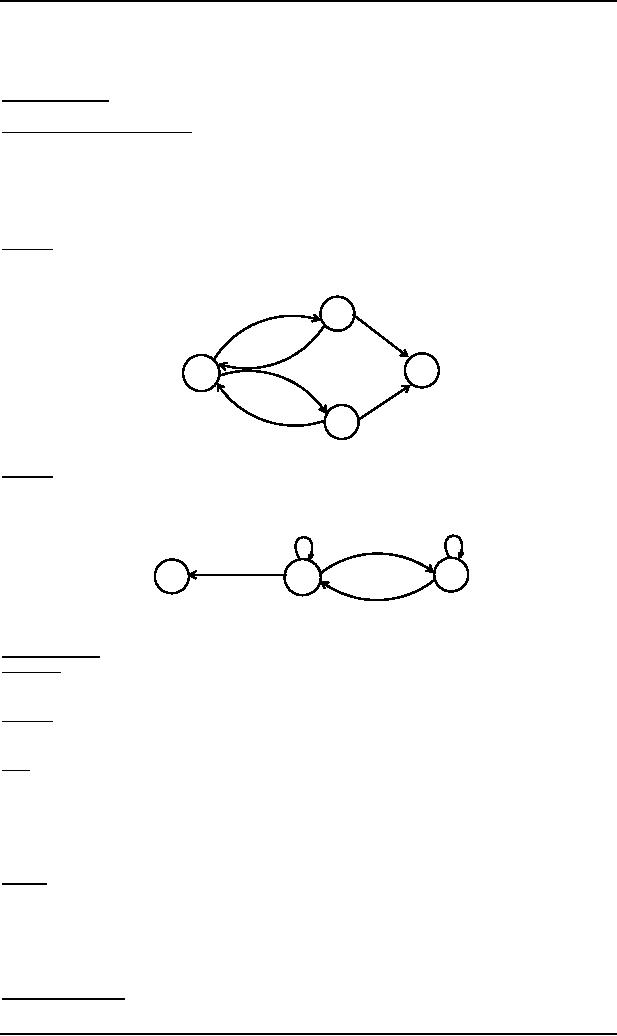
Consider
the following CFG
S ∆ aA|bB
A ∆ aS|a
B ∆ bS|b
A
then
the corresponding TG will be
a
a
a
+
S-
b
b
b
B
+
The
corresponding RE may be (aa+bb) .
Example
Consider
the following CFG
S ∆ aaS|bbS|abX|baX|L
X ∆ aaX|bbX|abS|baS,
aa,bb
aa,bb
then
the corresponding TG will be
ab,ba
L
X
+
S-
ab,ba
The
corresponding language is
EVEN-EVEN.
Null
Production
Definition
The
production of the form nonterminal
∆ L
is
said to be null
production.
Example:
Consider the CFG, S ∆ aA|bB|L, A ∆ aa|L, B ∆ aS
Here S ∆ L and A
∆ L
are
null productions.
Note
If a CFG
has a null production, then it is
possible to construct another
CFG without null production
accepting
the
same language with the
exception of the word L i.e.
if
the language contains the
word L then
the new
language
cannot have the word
L.
Following
is a method to construct a CFG
without null production for
a given CFG
Method
Delete
all the Null productions and
add new productions e.g.
consider
the productions of a certain CFG X ∆ aNbNa, N ∆ L, delete
the production N ∆ L and using
the
production
X ∆
aNbNa,
add the new productions X ∆ aNba, X
∆
abNa
and X ∆ aba
Thus the
new CFG will contain the
productions X ∆ aNba|abNa|aba|aNbNa
Note: It is to be
noted that X ∆ aNbNa
will still be included in
the new CFG.
Nullable
Production
104
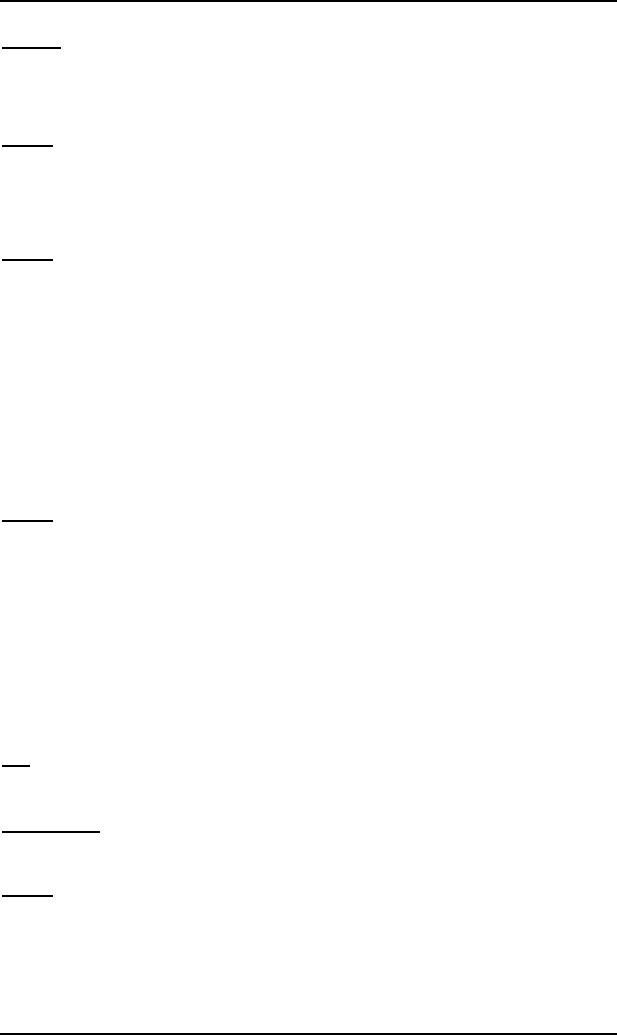
Theory of
Automata
(CS402)
Definition
A
production is called nullable
production if it is of
the form N ∆
L
or
there is
a derivation that starts at N
and leads to L i.e.
N1 ∆ N2, N2 ∆ N3, N3 ∆ N4, ..., Nn
∆L, where
N, N1, N2,
..., Nn are non terminals.
Example
Consider
the following CFG
S ∆ AA|bB, A
∆
aa|B, B
∆
aS |
L
Here S ∆ AA and A
∆
B
are nullable productions, while B
∆ L
is
null a production.
Following
is an example describing the method to
convert the given CFG
containing null productions and
nullable
productions into the one
without null productions
Example
Consider
the following CFG
S ∆ XaY|YY|aX|ZYX
X ∆ Za|bZ|ZZ|Yb
Y ∆ Ya|XY|L
Z ∆ aX|YYY
It is to be
noted that in the given CFG,
the productions S ∆ YY, X
∆
ZZ, Z
∆
YYY
are Nullable productions,
while Y
∆ L
is
Null production.
Here the
method of removing null productions, as
discussed earlier, will be used along
with replacing
nonterminals
corresponding to nullable productions like
nonterminals for null productions are
replaced.
Thus the
required CFG will be
S ∆XaY|Xa|aY|a|YY|Y|aX|ZYX|YX|ZX|ZY
X ∆ Za|a|bZ|b|ZZ|Z|Yb
Y ∆ Ya|a|XY|X|Y
Z ∆ aX|a|YYY|YY|Y
Example
Consider
the following CFG
S ∆ XY, X
∆
Zb, Y
∆
bW
Z ∆ AB, W
∆
Z, A
∆
aA|bA|L
B ∆Ba|Bb|L.
Here A ∆ L and B
∆ L
are
null productions, while Z ∆ AB, W
∆
Z
are nullable productions. The
new CFG
after,
applying the method, will
be
S ∆ XY
X ∆ Zb|b
Y ∆ bW|b
Z ∆ AB|A|B
W∆Z
A ∆ aA|a|bA|b
B ∆Ba|a|Bb|b
Note
While
adding new productions all
Nullable productions should be handled
with care. All Nullable
productions
will be
used to add new productions, but
only the Null production
will be deleted.
Unit
production
The
productions of the form nonterminal
∆
one
nonterminal, is called the unit
production.
Following
is an example showing how to
eliminate the unit productions
from a given CFG.
Example
Consider
the following CFG
S ∆ A|bb
A ∆ B|b
B ∆ S|a
Separate
the unit productions from
the nonunit productions as shown
below
105

Theory of
Automata
(CS402)
unit
prods.
nonunit
prods.
S∆A
S ∆ bb
A∆B
A∆b
B∆S
B∆a
S ∆ A gives S
∆
b
(using A ∆ b)
S ∆ A ∆ B gives S
∆
a
(using B ∆ a)
A ∆ B gives A
∆
a
(using B ∆ a)
A ∆ B ∆ S gives A
∆
bb
(using S ∆ bb)
B ∆ S gives B
∆
bb
(using S ∆ bb)
B ∆ S ∆ A gives B
∆
b
(using A ∆ b)
Thus the
new CFG will be
S ∆ a|b|bb, A
∆
a|b|bb, B
∆
a|b|bb.
Which
generates the finite
language {a,b,bb}.
Chomsky
Normal Form
If a CFG
has only productions of the
form
nonterminal
∆
string of
two nonterminals
or
nonterminal
∆
one
terminal
then
the CFG is said to be in
Chomsky Normal Form
(CNF).
106
Table of Contents:
- What does automata mean, Introduction to languages
- Kleene Star Closure, Recursive definition of languages
- Regular Expression, Recursive definition of Regular Expression
- Equivalent Regular Expressions
- Finite Automaton
- Equivalent FAs
- FA corresponding to finite languages
- Examples of TGs: accepting all strings
- Generalized Transition Graphs
- Nondeterminism, Kleeneís Theorem
- Proof(Kleeneís Theorem Part II)
- Kleeneís Theorem Part III
- Concatenation of FAs
- Closure of an FA
- Nondeterministic Finite Automaton, Converting an FA to an equivalent NFA
- NFA with Null String
- NFA and Kleeneís Theorem
- NFA corresponding to Concatenation of FAs
- Distinguishable strings and Indistinguishable strings
- Finite Automaton with output, Moore machine
- Mealy machine
- Equivalent machines
- Mealy machines in terms of sequential circuit
- Regular languages, Complement of a language
- Nonregular languages
- Pumping Lemma
- Pumping Lemma version II
- Pseudo theorem
- Decidability
- finiteness of a language
- Context Free Grammar (CFG), CFG terminologies
- Trees
- Polish Notation (o-o-o)
- Total language tree, Regular Grammar
- Null Production
- Chomsky Normal Form (CNF)
- A new format for FAs
- Nondeterministic PDA
- PDA corresponding to CFG
- Conversion form of PDA
- Conversion Form, Joints of the machine
- Row language, Nonterminals
- Non-Context-Free language, Pumping lemma for CFLs
- Decidablity, Parsing Techniques
- Turing machine