 |
METHODS OF PROJECT EVALUATIONS, Net present value, Weighted Average Cost of Capital |
| << Capital Budgeting Definition and Process |
| METHODS OF PROJECT EVALUATIONS 2 >> |
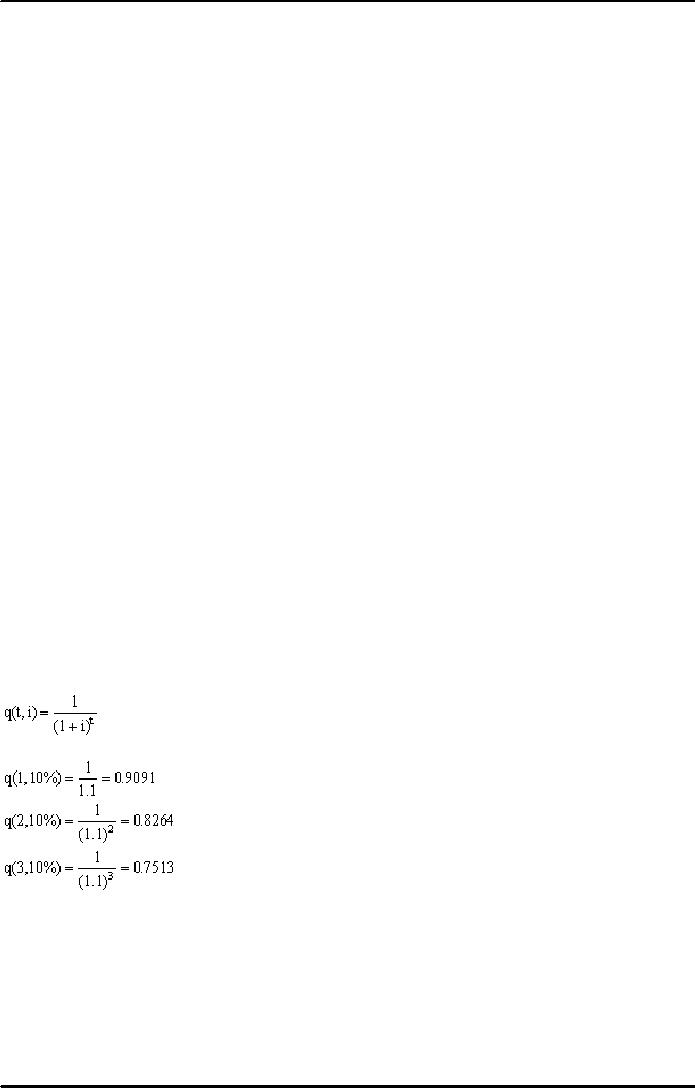
Corporate
Finance FIN 622
VU
Lesson
09
METHODS
OF PROJECT EVALUATIONS
The
following topics will be
discussed in this hand out.
Methods
of Project evaluations:
NPV
Associated
topics that will be covered
are:
Weighted
Average Cost of Capital
Opportunity
cost
Net
present value
(NPV)
There
are two aspects of NPV
method of project evaluation. First is the initial
investment or upfront cost
and
second, is the benefits (like cash
flow) emerging from the
project.
First
aspect is pretty simple. As it is
incurred in the current or present time, there
are no issues
associated
with
its measurement. On the other
side, benefits shall be reaped in
future and involves time
value of
money,
making the measurement complex and
difficult.
NPV
measures the NET benefit by which the
value of a firm would
increase in case the project
in
undertaken.
As on
overview of this method, the present
value of future cash flow is
calculated using a discount
rate.
And if
this PV of future cash flow is
greater than the initial investment, the
NPV is stated as "positive".
Alternatively,
this suggests that project is
worth undertaking and financially viable.
If the PV of future cash
flow
is less than initial investment,
then it is better to scrap the
project.
The
NPV method is used for evaluating the
desirability of investments or projects.
Net Present Value is
found
by subtracting the required investment:
NPV =
PV required investment
The
building worth Rs.
2,000,000, but this does not
mean that you are
Rs. 2,000,000 better off.
You
committed
Rs. 1,900,000, and therefore
your net present value is
calculated by using the above
formula:
NPV =
2,000,000 1,900,000 = Rs.
100,000
In
other words, your office
development is worth more than it costs,
it makes a net contribution to
value.
The
formula for calculating NPV
can be written as:
NPV = Co + C1
/ 1 + r
Where:
Co = the
cash flow at time o or investment and
therefore cash outflow
r = the discount
rate/the required minimum rate of
return on investment
The
discount factor r can be calculated
using:
Examples:
Decision
rule:
If NPV
is positive (+): accept the
project
If NPV
is negative (-): reject the
project
Weighted
Average Cost of
Capital:
A calculation of a
firm's cost of capital in which
each category of capital is
proportionately weighted.
All
capital
sources - common stock, preferred stock,
bonds and any other
long-term debt - are included in
a
27

Corporate
Finance FIN 622
VU
WACC
calculation.
WACC
is calculated by multiplying the cost of
each capital component by its
proportional weight and
then
summing:
WACC =
E / V * Re + D / V * Rd * ( 1 Tc )
Where:
Re =
cost of equity
Rd =
cost of debt
E =
market value of the firm's equity
D =
market value of the firm's
debt
V=E+D
E/V =
percentage of financing that is
equity
D/V =
percentage of financing that is
debt
Tc = corporate tax
rate
Broadly
speaking, a company's assets
are financed by either debt or equity.
WACC is the average of the
costs
of these sources of financing, each of
which is weighted by its respective
use in the given situation. By
taking
a weighted average, we can see how
much interest the company
has to pay for every
dollar it
finances.
A firm's
WACC is the overall required return on
the firm as a whole and, as
such, it is often used
internally
by
company directors to determine the
economic feasibility of expansionary
opportunities and mergers. It
is
the appropriate
discount rate to use for
cash flows with risk that is
similar to that of the overall
firm.
Opportunity
Cost:
The
cost of an alternative that must be
forgone in order to pursue a certain
action is called opportunity
cost.
Put another
way, the benefits you could have
received by taking an alternative
action.
There is a
difference in return between a chosen
investment and one that is
necessarily passed up. Say
you
invest in a
stock and it returns a
paltry 2% over the year. In
placing your money in the
stock, you gave up
the
opportunity of another investment - say, a risk-free
government bond yielding 6%. In this
situation,
your
opportunity costs are 4%
(6%-2%).
The
opportunity cost of going to
college is the money you
would have earned if you
worked instead. On the
one
hand, you lose four
years of salary while getting
your degree; on the other
hand, you hope to earn
more
during
your career, thanks to your
education, to offset the lost
wages.
Here's
another example: if a gardener decides to
grow carrots, his or her
opportunity cost is the
alternative
crop
that might have been
grown instead (potatoes,
tomatoes, pumpkins, etc.).
In
both cases, a choice between
two options must be made. It
would be an easy decision if
you knew the
end
outcome; however, the risk that you could
achieve greater "benefits"
(be they monetary or otherwise)
with
another option is the opportunity
cost.
28
Table of Contents:
- INTRODUCTION TO SUBJECT
- COMPARISON OF FINANCIAL STATEMENTS
- TIME VALUE OF MONEY
- Discounted Cash Flow, Effective Annual Interest Bond Valuation - introduction
- Features of Bond, Coupon Interest, Face value, Coupon rate, Duration or maturity date
- TERM STRUCTURE OF INTEREST RATES
- COMMON STOCK VALUATION
- Capital Budgeting Definition and Process
- METHODS OF PROJECT EVALUATIONS, Net present value, Weighted Average Cost of Capital
- METHODS OF PROJECT EVALUATIONS 2
- METHODS OF PROJECT EVALUATIONS 3
- ADVANCE EVALUATION METHODS: Sensitivity analysis, Profitability analysis, Break even accounting, Break even - economic
- Economic Break Even, Operating Leverage, Capital Rationing, Hard & Soft Rationing, Single & Multi Period Rationing
- Single period, Multi-period capital rationing, Linear programming
- Risk and Uncertainty, Measuring risk, Variability of return–Historical Return, Variance of return, Standard Deviation
- Portfolio and Diversification, Portfolio and Variance, Risk–Systematic & Unsystematic, Beta – Measure of systematic risk, Aggressive & defensive stocks
- Security Market Line, Capital Asset Pricing Model – CAPM Calculating Over, Under valued stocks
- Cost of Capital & Capital Structure, Components of Capital, Cost of Equity, Estimating g or growth rate, Dividend growth model, Cost of Debt, Bonds, Cost of Preferred Stocks
- Venture Capital, Cost of Debt & Bond, Weighted average cost of debt, Tax and cost of debt, Cost of Loans & Leases, Overall cost of capital – WACC, WACC & Capital Budgeting
- When to use WACC, Pure Play, Capital Structure and Financial Leverage
- Home made leverage, Modigliani & Miller Model, How WACC remains constant, Business & Financial Risk, M & M model with taxes
- Problems associated with high gearing, Bankruptcy costs, Optimal capital structure, Dividend policy
- Dividend and value of firm, Dividend relevance, Residual dividend policy, Financial planning process and control
- Budgeting process, Purpose, functions of budgets, Cash budgets–Preparation & interpretation
- Cash flow statement Direct method Indirect method, Working capital management, Cash and operating cycle
- Working capital management, Risk, Profitability and Liquidity - Working capital policies, Conservative, Aggressive, Moderate
- Classification of working capital, Current Assets Financing – Hedging approach, Short term Vs long term financing
- Overtrading – Indications & remedies, Cash management, Motives for Cash holding, Cash flow problems and remedies, Investing surplus cash
- Miller-Orr Model of cash management, Inventory management, Inventory costs, Economic order quantity, Reorder level, Discounts and EOQ
- Inventory cost – Stock out cost, Economic Order Point, Just in time (JIT), Debtors Management, Credit Control Policy
- Cash discounts, Cost of discount, Shortening average collection period, Credit instrument, Analyzing credit policy, Revenue effect, Cost effect, Cost of debt o Probability of default
- Effects of discounts–Not effecting volume, Extension of credit, Factoring, Management of creditors, Mergers & Acquisitions
- Synergies, Types of mergers, Why mergers fail, Merger process, Acquisition consideration
- Acquisition Consideration, Valuation of shares
- Assets Based Share Valuations, Hybrid Valuation methods, Procedure for public, private takeover
- Corporate Restructuring, Divestment, Purpose of divestment, Buyouts, Types of buyouts, Financial distress
- Sources of financial distress, Effects of financial distress, Reorganization
- Currency Risks, Transaction exposure, Translation exposure, Economic exposure
- Future payment situation – hedging, Currency futures – features, CF – future payment in FCY
- CF–future receipt in FCY, Forward contract vs. currency futures, Interest rate risk, Hedging against interest rate, Forward rate agreements, Decision rule
- Interest rate future, Prices in futures, Hedging–short term interest rate (STIR), Scenario–Borrowing in ST and risk of rising interest, Scenario–deposit and risk of lowering interest rates on deposits, Options and Swaps, Features of opti
- FOREIGN EXCHANGE MARKET’S OPTIONS
- Calculating financial benefit–Interest rate Option, Interest rate caps and floor, Swaps, Interest rate swaps, Currency swaps
- Exchange rate determination, Purchasing power parity theory, PPP model, International fisher effect, Exchange rate system, Fixed, Floating
- FOREIGN INVESTMENT: Motives, International operations, Export, Branch, Subsidiary, Joint venture, Licensing agreements, Political risk