Median in Case of a Frequency Distribution of a Continuous Variable

<< WHAT IS STATISTICS?:DESIRABLE PROPERTIES OF THE MODE, THE ARITHMETIC MEAN

GEOMETRIC MEAN:HARMONIC MEAN, MID-QUARTILE RANGE >>

MTH001 Elementary Mathematics

LECTURE # 25:

· Median in case of a frequency distribution of a continuous variable

· Median in case of an open-ended frequency distribution

· Empirical relation between the mean, median and the mode

· Quantiles (quartiles, deciles & percentiles)

· Graphic location of quantiles.

Median in Case of a Frequency Distribution of a Continuous Variable:

In case of a frequency distribution, the median is given by the formula

h ⎛n ⎞

X = l + ⎜ - c⎟

f ⎝2 ⎠

Where

l =lower class boundary of the median class (i.e. that class for which the cumulative

frequency is just in excess of n/2).

h=class interval size of the median class

f =frequency of the median class

n=Σf (the total number of observations)

c =cumulative frequency of the class preceding the median class

Note:

This formula is based on the assumption that the observations in each class are evenly

distributed between the two class limits.

Example:

Going back to the example of the EPA mileage ratings, we have

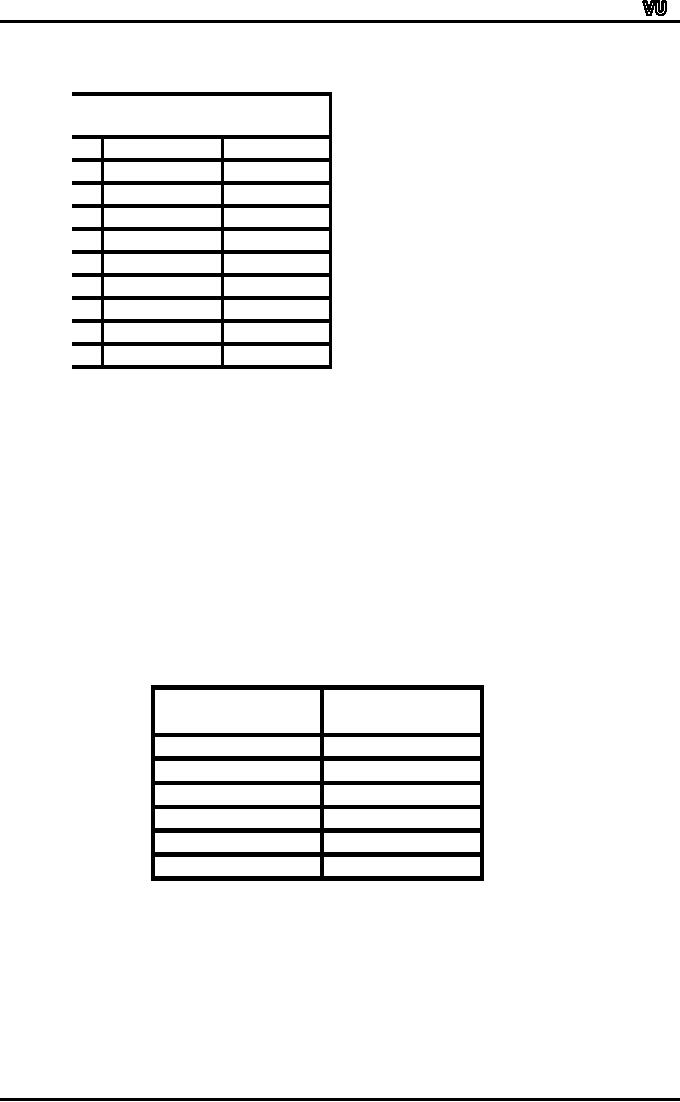
No.

Mileage

Class

Cumulative

Rating

Boundaries Frequency

Cars

30.0 32.9

29.95 32.95

33.0 35.9

32.95 35.95

36.0 38.9

35.95 38.95

39.0 41.9

38.95 41.95

42.0 44.9

41.95 44.95

In this example, n = 30 and n/2 = 15.

Thus the third class is the median class. The median lies somewhere between 35.95 and

38.95. Applying the above formula, we obtain

(15 - 6)

X = 35.95 +

= 35.95 + 1.93

= 37.88

~ 37.9

Interpretation:

Page

171

MTH001 Elementary Mathematics

This result implies that half of the cars have mileage less than or up to 37.88 miles per

gallon whereas the other half of the cars has mileage greater than 37.88 miles per gallon.

As discussed earlier, the median is preferable to the arithmetic mean when there are a few

very high or low figures in a series. It is also exceedingly valuable when one encounters a

frequency distribution having open-ended class intervals.

The concept of open-ended frequency distribution can be understood with the help of the

following example.

WAGES OF WORKERS

Example:

IN A FACTORY

Monthly Income

No. of

(in Rupees)

Workers

Less than 2000/-

100

2000/- to 2999/-

300

3000/- to 3999/-

500

4000/- to 4999/-

250

5000/- and above

Total

1200

In this example, both the first class and the last class are open-ended classes. This is so

because of the fact that we do not have exact figures to begin the first class or to end the

last class. The advantage of computing the median in the case of an open-ended frequency

distribution is that, except in the unlikely event of the median falling within an open-ended

group occurring in the beginning of our frequency distribution, there is no need to estimate

the upper or lower boundary. This is so because of the fact that, if the median is falling in an

intermediate class, then, obviously, the first class is not being involved in its

computation.The next concept that we will discuss is the empirical relation between the

mean, median and the mode. This is a concept which is not based on a rigid mathematical

formula; rather, it is based on observation. In fact, the word `empirical' implies `based on

observation'.

This concept relates to the relative positions of the mean, median and the

mode in case of a hump-shaped distribution. In a single-peaked frequency distribution, the

values of the mean, median and mode coincide if the frequency distribution is absolutely

symmetrical.

Page

172

MTH001 Elementary Mathematics

THE SYMMETRIC CURVE

Mean = Median = Mode

But in the case of a skewed distribution, the mean, median and mode do not all lie on the

same point. They are pulled apart from each other, and the empirical relation explains the

way in which this happens. Experience tells us that in a unimodal curve of moderate

skewness, the median is usually sandwiched between the mean and the mode.

The second point is that, in the case of many real-life data-sets, it has been

observed that the distance between the mode and the median is approximately double of

thf distance between the median and the mean, as shown below:

This diagrammatic picture is equivalent to the following algebraic expression:

Median - Mode

2 (Mean - Median) ---- (1)

The above-mentioned point can also be expressed in the following way:

Mean Mode =

3 (Mean Median)

---- (2)

Equation (1) as well as equation (2) yields the approximate relation given below:

EMPIRICAL RELATION BETWEEN

THE MEAN, MEDIAN AND THE MODE :

Mode = 3 Median 2 Mean

An exactly similar situation holds in case of a moderately negatively skewed distribution.

An important point to note is that this empirical relation does not hold in case of a

J-shaped or an extremely skewed distribution.

Let us now extend the concept of partitioning of the frequency distribution by

taking up the concept of quantiles (i.e. quartiles, deciles and percentiles).

Page

173

MTH001 Elementary Mathematics

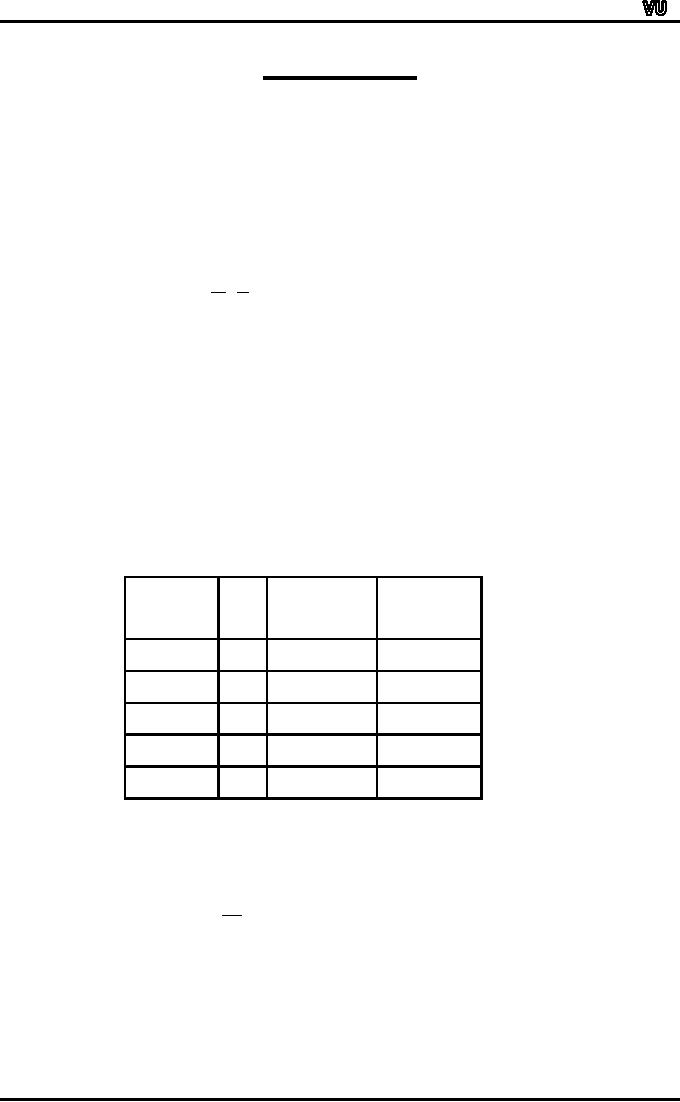
We have already seen that the median divides the area under the frequency polygon into

two equal halves:

50%

Median

A further split to produce quarters, tenths or hundredths of the total area under the

frequency polygon is equally possible, and may be extremely useful for analysis. (We are

often interested in the highest 10% of some group of values or the middle 50% another.)

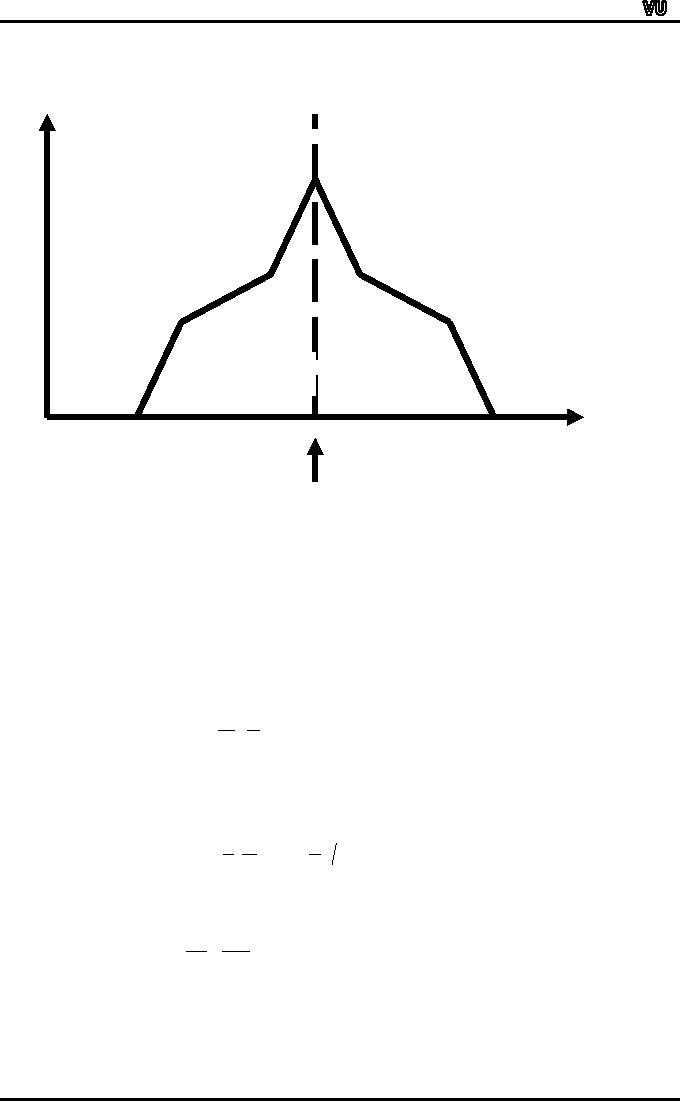
QUARTILES

The quartiles, together with the median, achieve the division of the total area into four equal

parts.

The first, second and third quartiles are given by the formulae:

First quartile:

⎛n

⎞

Q1 = l +

⎜ - c⎟

⎝4

⎠

Second quartile (i.e. median):

h⎛2n ⎞ h

Q =l+ ⎜ -c⎟=l+ (n 2-c)

f⎝4 ⎠ f

Third quartile:

h ⎛ 3n

⎞

= l +

- c⎟

⎜

f ⎝ 4

⎠

It is clear from the formula of the second quartile that the second quartile is the same as the

median.

Page

174

MTH001 Elementary Mathematics

25% 25% 25% 25%

Q1 Q2 = X Q3

DECILES & PERCENTILES

The deciles and the percentiles given the division of the total area into 10 and 100 equal

parts respectively.

The formula for the first decile is

h⎛ n ⎞

D1 = l + ⎜ - c⎟

The formulae for the subsequent deciles afe⎝10

⎠

h ⎛ 2n ⎞

D2 = l + ⎜ - c⎟

f ⎝ 10 ⎠

h ⎛ 3n

⎞

D3 = l +

- c⎟

⎜

f ⎝ 10

⎠

and so on.

It is easily seen that the 5th decile is the same quantity as the median.

The formula for the first percentile is

h⎛ n ⎞

P =l+ ⎜ -c⎟

f ⎝100 ⎠

The formulae for the subsequent percentiles are

h ⎛ 2n

⎞

P2 = l + ⎜

- c⎟

f ⎝100 ⎠

⎛ 3n

⎞

P3 = l +

- c⎟

⎜

⎝ 100

⎠

and so on.

Again, it is easily seen that the 50th percentile is the same as the median, the 25th

percentile is the same as the 1st quartile, the 75th percentile is the same as the 3rd quartile,

the 40th percentile is the same as the 4th decile, and so on.

All these measures i.e. the median, quartiles, deciles and percentiles are

collectively called quantiles. The question is, "What is the significance of this concept of

partitioning? Why is it that we wish to divide our frequency distribution into two, four, ten or

hundred parts?"

Page

175

MTH001 Elementary Mathematics

The answer to the above questions is: In certain situations, we may be interested in

describing the relative quantitative location of a particular measurement within a data set.

Quantiles provide us with an easy way of achieving this. Out of these various quantiles, one

of the most frequently used is percentile ranking.

Let us understand this point with the help of an example.

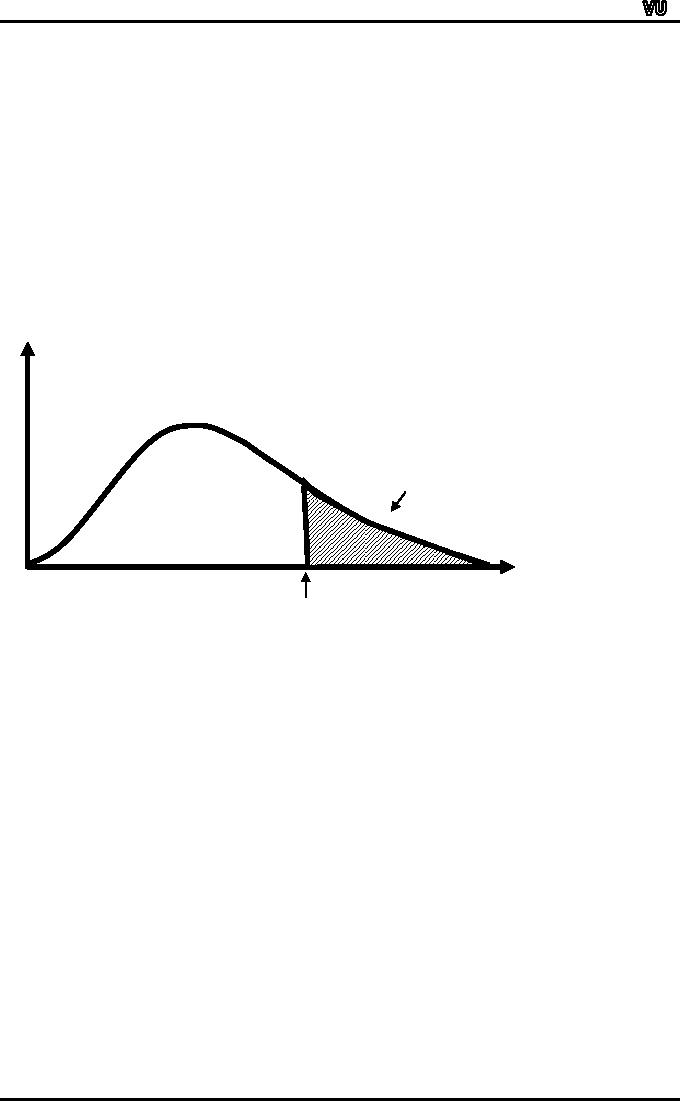
EXAMPLE:

If oil company `A' reports that its yearly sales are at the 90th percentile of all companies in

the industry, the implication is that 90% of all oil companies have yearly sales less than

company A's, and only 10% have yearly sales exceeding company A's:

This is demonstrated in the following figure:

Rel

ativ

Fre

que

ncy

0.10

0.90

Yearly

Company A's sales

(90th percentile)

It is evident from the above example that the concept of percentile ranking is quite a useful

concept, but it should be kept in mind that percentile rankings are of practical value only for

large data sets.

It is evident from the above example that the concept of percentile ranking is quite a useful

concept, but it should be kept in mind that percentile rankings are of practical value only for

large data sets.

The next concept that we will discuss is the graphic location of quantiles.

Let us go back to the example of the EPA mileage ratings of 30 cars

that

was

discussed in an earlier lecture. The statement of the example was:

EXAMPLE:

Suppose that the Environmental Protection Agency of a developed country performs

extensive tests on all new car models in order to determine their mileage rating.

Suppose that the following 30 measurements are obtained by conducting such tests on a

particular new car model.

Page

176

MTH001 Elementary Mathematics

ILEAGE RATINGS ON 30 CARS (MILES PER

GALLON)

42.1

44.9

37.5

32.9

40.0

40.2

35.6

35.9

38.8

38.6

38.4

40.5

39.0

37.0

36.7

37.1

34.8

33.9

38.1

39.8

When the above data was converted to a frequency distribution, we obtained:

Class Limit

Frequency

30.0 32.9

33.0 35.9

36.0 38.9

39.0 41.9

42.0 44.9

Also, we considered the graphical representation of this distribution.

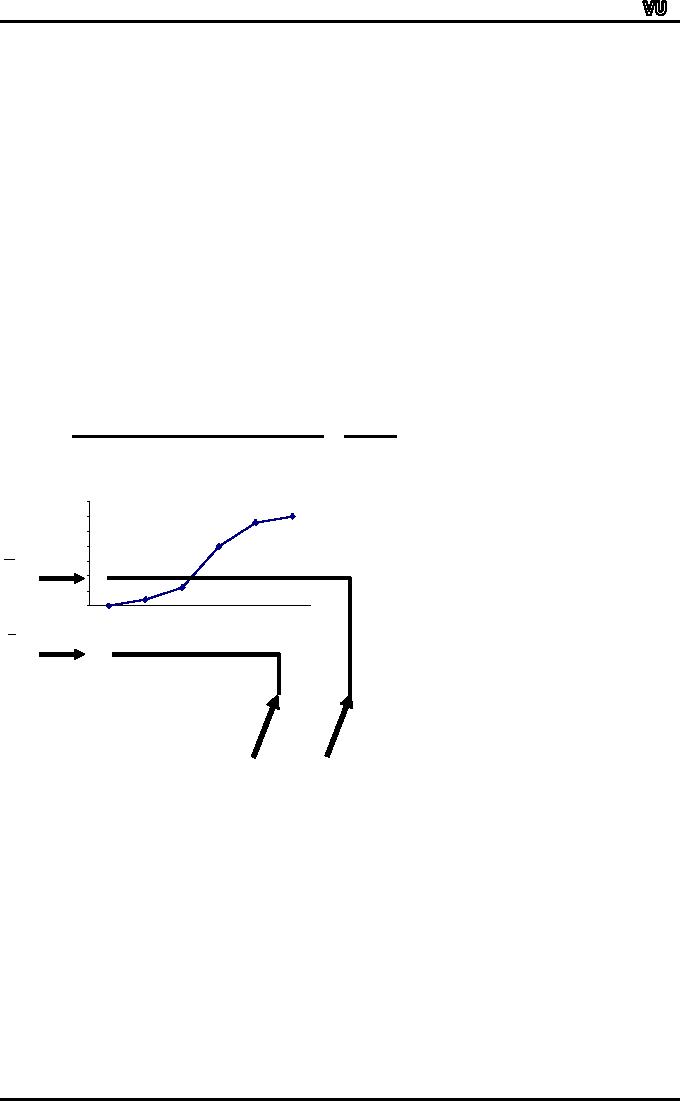
The cumulative frequency polygon of this distribution came out to be as shown in the

following figure:

Page

177

MTH001 Elementary Mathematics

Cumulative Frequency Polygon or OGIVE

This ogive enables us to find the median and any other quantile that we may be interested in

very conveniently. And this process is known as the graphic location of quantiles.

Let us begin with the graphical location of the median:

Because of the fact that the median is that value before which half of the data

lies, the first step is to divide the total number of observations n by 2.

In this example:

n 30

= 15

2 2

The next step is to locate this number 15 on the y-axis of the cumulative frequency polygon.

Cumulative Frequency Polygon or OGIVE

Page

178

MTH001 Elementary Mathematics

Lastly, we drop a vertical line from the cumulative frequency polygon down to the x-axis.

Cumulative Frequency Polygon or OGIVE

Now, if we read the x-value where our perpendicular touches the x-axis, students, we find

that this value is approximately the same as what we obtained from our formula.

Cumulative Frequency Polygon or OGIVE

X = 37.9

It is evident from the above example that the cumulative frequency polygon is a very useful

device to find the value of the median very quickly.In a similar way, we can locate the

Page

179

MTH001 Elementary Mathematics

quartiles, deciles and percentiles.To obtain the first quartile, the horizontal line will be drawn

against the value n/4, and for the third quartile, the horizontal line will be drawn against the

value 3n/4.

Cumulative Frequency Polygon or OGIVE

For the deciles, the horizontal lines will be against the values n/10, 2n/10, 3n/10, and so on.

And for the percentiles, the horizontal lines will be against the values n/100, 2n/100, 3n/100,

and so on.

The graphic location of the quartiles as well as of a few deciles and percentiles

for the data-set of the EPA mileage ratings may be taken up as an exercise:

This brings us to the end of our discussion regarding quantiles which are sometimes also

known as fractiles --- this terminology because of the fact that they divide the frequency

distribution into various parts or fractions.

Page

180

Table of Contents: