 |
Linear Programming:PRESENTATION IN TABULAR FORM - (SIMPLEX TABLE) |
| << Linear Programming:SIMPLEX METHOD, Simplex Procedure |
| Linear Programming:ARTIFICIAL VARIABLE TECHNIQUE >> |
Operations
Research (MTH601)
118
Now a
question may arise whether
the above solution constitutes
the best or optimal
solution.
Examining
the objective function
Z
+
2 S2 + 3 S3 = 240,
we
observe that the coefficients of
the non-basic variables
S2 and S3 are positive on the left
hand side and this is
the
indication
to stop the iteration. Hence
we conclude that Z
=
240 will be the maximum
value of Z
and
the solution set
can
be written as
Z*
=240
x
=
30
y
=
30
S1 = 40
S2 = 0
S3 = 0
PRESENTATION
IN TABULAR FORM - (SIMPLEX
TABLE)
The
relevant information of first example may
be presented in a concise form as what we
call 'Simplex
table'
instead of writing down th
set of equations in full
symbols for the variables in
each of the equations. The
given
linear
programming problem is expressed in a
standard form including
slack variables. Then we
write the
coefficients
of the variables and the
right hand side in the
table.
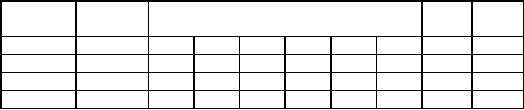
The
above example is presented in
the following tabular form.
This is the initial
table.
RHS
Ratio
Equation
Basic
Coefficient
of
S2
S3
No.
Variable
Z
x
y
S1
0
-
1
-3
-5
0
0
0
0
-
1
0
1
0
1
0
0
40
∞
S1
2
0
0
1
0
1
0
30
30
S2
3
0
1
1
0
0
1
60
60
S3
Solution:
Z
=
0, S1 = 40, S2 = 30, S3 = 60, x
= y = 0
The
basic procedure when using
the simplex table is the
same as before. We give below
the steps of the
simplex
method that would be applied
to prepare the next table
from the initial
table.
STEP
1
To
select the entering basic
variable: Consider
the first row corresponding
to the equation 0 of the
table. If the
problem
is one to maximize the
effectiveness (profit), the
variable with the most
negative coefficient is selected
as
118
Operations
Research (MTH601)
119
the
new entering basic variable.
The column corresponding to the
most negative coefficient -5 is 'y'
and
the same
is
marked as a key
column indicating
that y
is
the new entering basic
variable.
STEP
2
To
select the leaving basic
variable: Now
consider all the rows except
the first row. Formulate
the ratio in each
row
by taking right hand side of each
row and dividing by the
corresponding element of the
key column. The
ratios
in
this example are 40/0 = ∞,
30/1 = 30, 60/1 = 60.
Select the least non-negative
ratio.
In this example the
minimum
non-negative
ration corresponds to the
row 2 indicating that S2 is the leaving basic
variable and this row
containing
S2 as the basic variable is
marked as a key
row. The
element at the intersection of
key column and key row is
called
the
key number or pivot number.
In this example the key
number is 1. If this is not 1, the
same can be made 1 by
dividing
the same row
suitably.
STEP
3
Elimination
of coefficients in the key
column: Gauss
Jordan elimination requires
that all the elements in
the key
column
except the key row
should vanish. Suitably multiplying
coefficients of the key row
and adding the same
to
the
corresponding coefficients of the
other rows achieve this
result.
In
this example, multiply the
key row by 5 and add this
resulting row to the row 0.
To get rid of the coefficient of
y
in
the second row, next
multiply the key row by 0
and add to the row 1
and similarly multiply the
key row by -1 and
add
to the row 3 to eliminate the coefficient
of y
in
the third row. So all the
key column elements are thus
made 0 in
all
the rows except the key
row. The resulting table is
presented. Note that y has
entered the basis and
S2 has left.
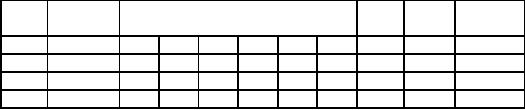
This
is the first
iteration
y
enters
the basis and S2 leaves the
basis
Iteration
I:
RHS
Ratio
Solution
Eqn.
Basic
Coefficient
of
S1 S2
S3
No.
Variable
Z
x
y
0
-
1
-3
0
0
5
0
150
-
Z=150
1
0
1
0
1
0
0
40
40
S1=40
S1
2
0
0
1
0
1
0
30
∞
y=30
y
3
0
1
0
0
-1
1
30
30
S3=30
S3
STEP
4
Further
improvement of solution: After
every iteration, look at the
objective function row (row
0). Scan if there is
any
negative coefficients among variables in
this row for a maximization
problem. If there is a negative
coefficient,
this
is a clear indication that the
problem has not reached
the maximum value. Still
there is a scope of improving
the
existing
solution. In this example, we have
the coefficient of x
in
the objective function row as -3 (a
negative)
indicating
that x
can
be selected as the new entering
basic variable. Mark this column as
key column and
another
iteration
is required. So find the
ratio in each of the rows 1, 2
and 3. We have, the ratios
40, ∞
and
30 as indicated in
the
table under the column
ratio. Select the row
corresponding to least non-negative
value (i.e.) 30, (row
3). So S3 is
the
leaving variable and this
key row is marked and
the same procedure of
eliminating the coefficients of x in
the
119
Operations
Research (MTH601)
120
key
column is performed by multiplying the
key row by 3, -1 and 0 and
adding to the row 0, 1 and
2
respectively.
The result is presented in
the table below.
STEP
5
Stopping
rule: The
row 0 has all coefficients of
the variables as non-negative. If
there is no negative coefficient
in
this
row, this is an indication that the
problem has reached the
maximum value and this is
the optimal solution to
the
linear
programming problem.
Note:
If
the problem is one of
minimization subject to constraints of
< sign, the criterion for
selecting the
entering
variable
is to pick the variable in
the objective row with
the most positive coefficient. It all of
them are negative or
0,
this suggests that the
present solution is the
optimum.
120
Operations
Research (MTH601)
121
REVIEW
QUESTIONS
1.
A
manufacturer has two
products P1 and P2 both or which are
produced in two steps by
machines
M1 and M2. The process times
per hundred for the
products on the machines
are:-
Products
M1
M2
Contribution
(per
100 units)
4
5
Rs.
10
P1
5
2
Rs.
5
P2
Available
hrs
100
80
The
manufacturer is in a market upswing and
can sell as much as he can
produce of both
products.
Formulate
the mathematical model and
determine optimum product
mix using simplex
method.
2.
The
ABC company, a manufacturer of
test equipment has three
major departments for
its
manufacture
of X-10
model and X-20
model. Monthly capacities
are given as
follows:-
Time
required
per
unit
Hours
available
X-10
Model
X-20
Model
this
month
Main
Frame
4.0
2.0
1,600
Department
Electrical
Wiring
2.5
1.0
1,200
Department
Assembly
Department
4.5
1.5
1,600
The
contribution of the X-10
model is Rs. 40/- each
and the contribution of the
X-20
model is Rs. 10/-
each.
Assuming
that the company can sell
any quantity of either
product due to favorable
conditions, find:
(i)
the optimal output for
both models with the
help of simplex
method
(ii)
the highest possible contribution
for this month.
(iii)
the slack time in the
three departments.
3.
A
manager produces three items
A,
B and
C.
He has the possibility of applying
two strategies -
produce
all the three items or
any two of them. Products
A
and
C
pass
through shops I and II,
whereas B
is
further
processed in shop III. Each
shop has limited available
hours. Hours available in shops I, II
and III
are
162 hours, 189 hours
and 5 hours respectively.
Profit per unit from
A,
B and
C
is
Rs. 27/-, Rs. 29/-
and
Rs.
25/- respectively. The
following table gives the
processing time of different items in
different shops.
Items
Shops
A
B
C
I
27
12
12
II
27
15
25
121
Operations
Research (MTH601)
122
III
0
3
0
Find
the optimum production of
A,
B and
C
so
as to maximize profit.
4.
The
ABC
manufacturing
company can make two
products P1 and P2. Each of the products
requires
time
on a cutting machine and a finishing
machine.
Product
P1
P2
Cutting
hours (per unit)
2
1
Finishing
hours (per unit)
3
3
Profit
per unit
Rs.
6
Rs.
4
Maximum
sales (unit per week)
-
200
The
number of cutting hours available
per week is 390 and number
of finishing hours available
per week is
810.
How much should be produced
of each product in order to
achieve maximum profit for
the company?
5.
A
manufacturer can produce
three products A,
B and
C
which
pass through different machines
M1,
M2 and M3. Available machines for
each product and the
requirement of machine time
for each product is
given
in the matrix below.
Machine
time
Products
Available
time
in
hours
A
B
C
in
hours
1
2
2
1,900
M1
3
2
4
2,100
M2
3
2
-
1,500
M3
If
the profit of each unit of
A,
B and
C
is
respectively Rs. 5, Rs. 4
and Rs. 6, find how
many units of each
product
should be produced so that
the profit will be
maximum.
6.
A
firm produces 3 products
A,
B and
C
using
same type of materials
L,
M,
and N.
The specific
consumption
of each material for unit
production is given in the
table. The profits of A,
B and
C
are
respectively
Rs. 70, Rs. 50 and
Rs. 60.
Material
Quantity
required per unit
Available
of
production
Material
2
1
3
80
L
4
4
1
240
M
3
4
2
160
N
122
Operations
Research (MTH601)
123
(a)
Find
the suitable production
programme so as to maximize the
profit.
(b)
What
type of surplus material
would be available? Can you
utilize materials?
(c)
Find
the production pattern
(revised) and profit
theorem.
7.
A
material manufacturing firm
has discontinued production of a
certain unprofitable product
line.
This
created considerable excess
production capacity. Management is
considering to devote this
excess
capacity
to one or more of three
products; call them products
1, 2 and 3. The available
capacity on the
machines
which limit output is
summarized in the following
table.
Available
time
Machine
type
(in
machine-hour per
week)
Milling
machine
250
Lathe
150
Grinder
50
The
number of machine-hours required
for each unit of the
respective products is given
below.
Productivity
(in machine hours per
unit)
Machine
type
Product
1 Product 2
Product
3
Milling
machine
8
2
3
Lathe
4
3
0
Grinder
2
-
1
The
unit profit would be Rs.
20, Rs. 6 and Rs. 8
respectively for products 1, 2
and 3. Find how much
of
each
product the firm should
produce in order to maximize
profit.
8.
A
factory produces three products,
which are processed through
three different stages. The
time
required
to manufacture one unit of
each of the three products
and the daily capacity of
the stages are
given
in
the following table.
Time
per unit in
minutes
Stage
capacity
Stage
Product
1 Product 2 Product
3
(minutes)
1
1
2
1
430
2
3
-
2
460
3
1
4
-
420
Profit
per
3
2
5
unit
(Rs.)
(i)
Set
the data in a simplex
table.
(ii)
Find
the table of optimum
solution.
(iii)
State
from the tale-maximum
profit, production pattern
and surplus capacity of any
stage.
123
Operations
Research (MTH601)
124
(iv)
What
is the meaning of the shadow
price? Where is it shown in
the table? Explain it in
respect
of
resources of stages
having
shadow
price.
(v)
How
many units of other
resources will be required to completely
utilize the surplus
resource?
9.
Solve
the following problem using
simplex method:
Maximize
x0 = 2x1 + 3x2 + 4x3
Subject
to
2x1 +
x2 +
2x3 ≤
50
x1 +
3x2 +
x3 ≤
25
x1 +
2x2 +
x3 ≤
26
x2 , x3 ≥
0
x1 ,
10.
A
furniture company can produce four
types of chairs. Each chair
is first made in the
carpentry
shop
and then varnished, waxed
and polished in the
finishing shop. Manhours
required in each shop
are:
Chair
type
1
2
3
4
Carpentry
shop
4
9
7
10
Finishing
shop
1
1
3
40
Contribution
per
12
20
18
40
chair-Rs.
Total
number of man-hours available
per month in carpentry and
finishing shops are 6000
and 4000
respectively.
Assuming abundant the number of
chairs of different type produced so
that profit is
maximized
using the simplex
method.
11.
A
stereo equipment manufacturer
can produce two models A
and B of 40 and 80 watts total
music
power
each. Each model passes
through three different manufacturing
divisions 1, 2 and 3 where model
A
takes
4, 2.5 and 4.5 hrs
each and model B takes 2, 1
and 1.5 hrs each.
The three divisions have a
maximum
of
1600, 1200 and 1600
hours every month
respectively. Model A gives a
contribution of Rs. 400 each
and
B
gives Rs. 100 each. Assuming
abundant product demand,
find out the optimum
product mix and
the
maximum
contribution through simplex
method.
12.
A
company produces three
products P,
Q and
R
form
three raw materials
A,
B and
C.
One unit of
product
P
requires
2 units of A
and
3 units B.
A unit of product Q
requires
2 units of B
and
5 units of C
and
one
unit of product R
requires
3 units of A,
2 units of B
and
4 units of C.
The company has 8 units
of
material
A,
10 units of material B
and
15 units of material C
available
to it. Profits per unit of
products P,
Q
and
R
are
Rs. 3, Rs. 5 and Rs. 4
respectively.
a)
Formulate the problem
mathematically.
b)
How many units of each
product should be produced to
maximize profit?
13.
A
pharmaceutical company has
100 kg of A,
180 kg of B
and
120 kg of C
available
per month.
They
can use these materials to
make three products namely
5-10-5, 20-5-10, where the
numbers in each
124
Operations
Research (MTH601)
125
case
represent the percentage by
weight of A,
B and
C
respectively
in each of the product. The
cost of
the
raw materials are given
below.
Ingredient
A
B
C
Inert
Ingredient
Cost
per Kg (Rs.)
80
20
50
20
Selling
price of these products are
Rs. 40.5, Rs. 43 and
Rs. 45/kg respectively.
There is a capacity
restriction
that the product 5-10-5
cannot be produced more than
30 kg per month. Determine
how much of
each
product they should product
they should to maximize
their monthly profit.
125
Operations
Research (MTH601)
126
14.
Consider
the following linear
programming problem:
Maximize
x0 = 3x1 + 2x2 + 5x3
Subject
to
x1 +
2x2 +
2x3 ≤
8
3x1 +
2x2 +
6x3 ≤
12
2x1 +
3x2 +
4x3 ≤
12
x3 ≥
0
x1 ,
x2 ,
(i)
Solve
this problem by simplex
method.
(ii)
Does
this problem have an
alternative optimal
solution?
(iii)
The
validity of one of the steps
in simplex method becomes
questionable as you work out
this
problem.
What is this step?
15.
An
aviation fuel manufacturer sells
two types of fuel, A
and
B.
Type A
fuel
is 25 per cent grade
I
petrol,
25 per cent grade II petrol
and 50 per cent grade III
petrol. Type B
fuel
is 50 per cent grade
III
petrol.
Type B
fuel
is 50 per cent grade II
petrol and 50 percent grade
III petrol. Available for
production
are
2000 liters/hour of grade I
and 800 liters/hour of grade
II and III. The cost of
petrol is Rs. 3 per litre
for
grade
I, Rs. 6 per litre for
grade II and Rs. 5 per
litre for grade III. Type
A
can
be sold for Rs. 7.5
per litre
and
type B
for
Rs. 9.00 per litre.
How much of each fuel
should be made?
16.
A
manufacturer uses three raw
products a,
b, c priced
at 30, 50 and 120 rupees
per kg respectively.
He
can make three different
products A,
B and
C,
which can be sold at 90,
100 and 120 rupees
per kg
respectively.
The raw products can be
obtained only in limited
quantities, namely 20, 15
and 10 kg per day.
Given
2 kg of a
plus
1 kg of b
plus
1 kg c
will
yield 4 kg of A,
3 kg of a
plus
2 kg of b
plus
2 kg of c
will
yield
7 kg of B,
2 kg of b
plus
1 kg of c
will
yield 3 kg of C.
Make
a production plan, assuming
the order and cost
are not influenced by the
choice among the
alternatives.
Solve the problem by simplex
method.
126
Table of Contents:
- Introduction:OR APPROACH TO PROBLEM SOLVING, Observation
- Introduction:Model Solution, Implementation of Results
- Introduction:USES OF OPERATIONS RESEARCH, Marketing, Personnel
- PERT / CPM:CONCEPT OF NETWORK, RULES FOR CONSTRUCTION OF NETWORK
- PERT / CPM:DUMMY ACTIVITIES, TO FIND THE CRITICAL PATH
- PERT / CPM:ALGORITHM FOR CRITICAL PATH, Free Slack
- PERT / CPM:Expected length of a critical path, Expected time and Critical path
- PERT / CPM:Expected time and Critical path
- PERT / CPM:RESOURCE SCHEDULING IN NETWORK
- PERT / CPM:Exercises
- Inventory Control:INVENTORY COSTS, INVENTORY MODELS (E.O.Q. MODELS)
- Inventory Control:Purchasing model with shortages
- Inventory Control:Manufacturing model with no shortages
- Inventory Control:Manufacturing model with shortages
- Inventory Control:ORDER QUANTITY WITH PRICE-BREAK
- Inventory Control:SOME DEFINITIONS, Computation of Safety Stock
- Linear Programming:Formulation of the Linear Programming Problem
- Linear Programming:Formulation of the Linear Programming Problem, Decision Variables
- Linear Programming:Model Constraints, Ingredients Mixing
- Linear Programming:VITAMIN CONTRIBUTION, Decision Variables
- Linear Programming:LINEAR PROGRAMMING PROBLEM
- Linear Programming:LIMITATIONS OF LINEAR PROGRAMMING
- Linear Programming:SOLUTION TO LINEAR PROGRAMMING PROBLEMS
- Linear Programming:SIMPLEX METHOD, Simplex Procedure
- Linear Programming:PRESENTATION IN TABULAR FORM - (SIMPLEX TABLE)
- Linear Programming:ARTIFICIAL VARIABLE TECHNIQUE
- Linear Programming:The Two Phase Method, First Iteration
- Linear Programming:VARIANTS OF THE SIMPLEX METHOD
- Linear Programming:Tie for the Leaving Basic Variable (Degeneracy)
- Linear Programming:Multiple or Alternative optimal Solutions
- Transportation Problems:TRANSPORTATION MODEL, Distribution centers
- Transportation Problems:FINDING AN INITIAL BASIC FEASIBLE SOLUTION
- Transportation Problems:MOVING TOWARDS OPTIMALITY
- Transportation Problems:DEGENERACY, Destination
- Transportation Problems:REVIEW QUESTIONS
- Assignment Problems:MATHEMATICAL FORMULATION OF THE PROBLEM
- Assignment Problems:SOLUTION OF AN ASSIGNMENT PROBLEM
- Queuing Theory:DEFINITION OF TERMS IN QUEUEING MODEL
- Queuing Theory:SINGLE-CHANNEL INFINITE-POPULATION MODEL
- Replacement Models:REPLACEMENT OF ITEMS WITH GRADUAL DETERIORATION
- Replacement Models:ITEMS DETERIORATING WITH TIME VALUE OF MONEY
- Dynamic Programming:FEATURES CHARECTERIZING DYNAMIC PROGRAMMING PROBLEMS
- Dynamic Programming:Analysis of the Result, One Stage Problem
- Miscellaneous:SEQUENCING, PROCESSING n JOBS THROUGH TWO MACHINES
- Miscellaneous:METHODS OF INTEGER PROGRAMMING SOLUTION