 |
Inventory Control:SOME DEFINITIONS, Computation of Safety Stock |
| << Inventory Control:ORDER QUANTITY WITH PRICE-BREAK |
| Linear Programming:Formulation of the Linear Programming Problem >> |
Operations
Research (MTH601)
72
STEP 1:
Calculate
usage value by multiplying
annual usage of each item
with its unit cost
and tabulate them
and
assign
rank by giving rank to the
largest usage value as in
table below.
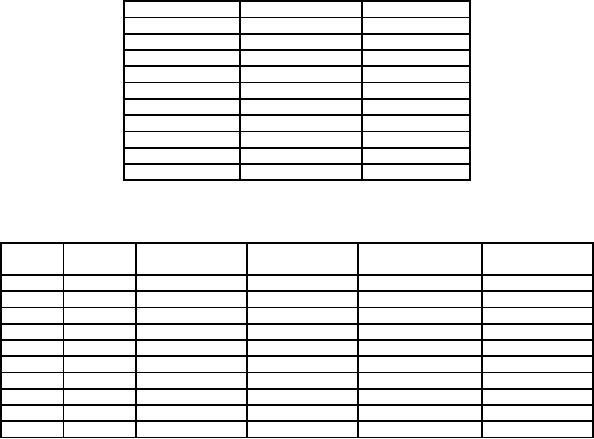
Items
No.
Annual
Usage
Ranking
1
3000
6
2
40500
1
3
300
9
4
5000
4
5
200
10
6
22000
2
7
800
7
8
4000
5
9
9000
3
10
700
8
STEP
2: Arrange
items as per ranking and
calculate cumulative usage
and % cumulative value as in
the table below.
%
of cumulative
Cumulative
%
Rank
Item
No.
Annual
usage
Cumulative
Annual
usage
Annual
usage
of
item
1
2
40500
40500
47
10
2
6
22000
62500
73
20
3
9
9000
71500
84
30
4
4
5000
76500
91
40
5
8
4000
80500
94.2
50
6
1
3000
83500
98
60
7
7
800
84300
98.6
70
8
10
700
85000
99.4
80
9
3
300
85300
99.8
90
10
5
200
85500
100
100
If
you draw the figure,
you will see that
the curve changes at points
(say) X and Y. The items
upto X is classified as
class
A items and between X and Y
as class B and the rest as
class C items.
SOME
DEFINITIONS
Lead-time:
This is
defined as the time interval
between the placing of the
orders and the actual
receipt of goods.
Lead-time
Demand: This
is the lead-time multiplied by
demand rate. For example, if
the lead-time is 3 weeks
and
the
demand is at the rate of 50
items per week, then
the lead-time demand is 3
x
50 = 150
items.
The
lead-time may not be
constant. For one batch, a
vendor may take 45 days
and for the next
batch 50 days and so
on.
Lead-time itself is therefore a
stochastic variable. This
complicates the problem of
accumulating stock over
the
period
encompassed by the lead-time.
Lead-time may also be
forecast exponentially as is done
with the demand.
Safety
stock or Buffer stock:
Lead-time
demand is the stock level,
which, on the average is
sufficient to satisfy
the
customer's
orders as the stocks are
being replenished. "On the
average" would mean that
during this period of
replenishment
50% of the customer's order
can be filled and the
remaining 50% may either be
refused or back
ordered
to be filled later. The
reason for this is obvious.
Forecast is after all a
point estimate only. If the
demand is
72
Operations
Research (MTH601)
73
greater
than the forecasts, the
customers would not be
serviced. If the demand is less
then the forecasts,
overstocking
would occur. When these
two variables, stock level
and service to the customer,
are summed up over
thousands
of stock level and service
to the customer, are becomes
a major problem for an
organisation to find an
acceptable
compromise between the two.
Sometimes the management in an
organisation would like to
limit the
disservice
to the customer down to 5% or
10% at the cost of extra
stocking. This extra stock
in excess of the
lead-
time
demand is called the safety
stock. Saftely stock may be
expressed as percentages of the
lead-time demand. It
may
be computed in different
ways.
Reorder
level: This
is defined as the level of
the inventory at which the
order is placed. It has
generally two
components
(i) Lead time Demand
and (ii) Safety
Stock.
Reorder
level (ROL) = Lead time
demand (LTD) + Safety stock
(SS).
Computation
of Safety Stock:
As
discussed earlier, if the
demand exceeds the forecast,
the result is bad service to
the customer and if the
demand
is
less than the forecast
figure, this results in
overstocking. Thus there is a
forecast error. This error
is assumed to be
normally
distributed, with zero mean.
If the standard deviation of
the forecast error is
calculated, then safety
stock
may
be set with the desired
confidence level to result in
not more the 5 or 10%
shortages etc.
There
is another measure of variation,
popularly known as mean
absolute deviation (MAD),
which can be computed
far
more easily. It can be
routinely smoothed every
period for obtaining better
estimates of the safety
stock.
MAD
is related to the standard
deviation for a normal
distribution as given
by.
MAD
=
2
š
SD.
SD
=
š 2MAD
Therefore,
Now
safety stock = Z
(S.D)
=
Z
š 2MAD
=
K
MAD
where
K is called service factor
K
=
Z
š 2
The
safety stock is for just
one period and has to be
extended over the lead
time. The necessary formula
has been
derived
by extensive simulation by statisticians
and is given below.
MADLT
= (0.659+ 0.341 LT)
MAD
Safety
stock over the
lead-time
=
K
(0.659
+
0.341
LT
) MAD
=
Z
š 2
(0.659 + 0.34
LT
)MAD
Example:
A company
uses annually 50000 units of
raw materials at a cost Rs.
1.2 per item. Ordering
cost of items is
Rs.
45 per order and item
carrying cost is 15% per
year of the average
inventory.
73
Operations
Research (MTH601)
74
1.
Find
the economic
quantity.
2.
Suppose
that the company follows
the EOQ policy and it
operates for 300 days a
year, that the
procurement
time is 12 days and mum,
minimum and average
inventories.
Solution:
D
= Demand = 50000/year
No.
of days = 300/year
C1
= Rs.
1.2 per item
Lead
time = 12 days
C2
= Rs. 45
per order
Safety
stock = 500
C3
= 15% of
Rs. 1.2/item/year.
=
Rs. 0.18 per item
per year.
2C2D
EOQ
=
(1)
C3
2×45×50000
=
0.18
=
25000000
=
5000
(2)
Requirement
per day = 50000/300
Lead
time demand = 12 x 500/3 =
2000
Safety
stock
=
500
Reorder
level
=
Lead time demand + safety
stock
=
2000 + 500 = 2500
Maximum
inventory = E.O.Q + Safety
stock
=
5000 + 500 = 5500
Minimum
inventory = Safety stock =
500
Average
inventory
=
(Max. Inv. + Min.
Inv.)/2
=
(5500 + 500)/2 = 3000
Example
A scrutiny of
past records gives the
following distributions for
lead time and daily
demand during lead
time.
Lead
time distribution
74

Operations
Research (MTH601)
75
Lead
time (days)
3
4
5
6
7
8
9
10
Frequency
2
3
4
4
2
2
2
1
Demand
distribution
Demand/day
(units)
0
1
2
3
4
5
6
7
Frequency
2
4
5
5
4
2
1
2
What
should be the buffer
stock?
Solution:
Computation
of average or mean lead
time.
∑
(Frequency
×
lead
time)
=
∑
Frequency
6+12+20+24+14+6+18+10
=
20
=
6
days
Average
demand
∑
(Frequency
×
demand/day)
=
∑
frequency
0+4+10+15+16+10+6+14
=
25
=3
Average
lead-time demand
=
Average lead time x Average
demand/day
=
6 x 3 = 18.
Maximum
lead-time demand.
=
Max. lead time x Max.
demand/day
=
10 x 7 = 70
∴
Buffer
stock = Max. lead time
demand - Average lead time
demand
*Example
7.7.3
For
a fixed order quantity
system find the EOQ,
SS, ROL and average
inventory for an item with
the
following
data.
Demand
= 10000 units
Cost
of item = Re. 1
Order
cost = Rs. 12
75

Operations
Research (MTH601)
76
Holding
cost = 24%
Post
lead times = 13 days
Solution:
2C2D
EOQ
=
(1)
C3
2×12×10000
=
=
1000
items
0.24×1
(2)
The
Average lead time = (13 + 14
+ 15 + 16 + 17)/5
=
15 days ( 30 days time is
omitted)
Maximum
lead time = 30 days
Safety
stock = ( 30 - 15) x 10000/(30 x
12) = 420
(3)
Reorder
level = Lead time demand +
Safety stock
=
417 + 420 = 837
(4)
Average
inventory = (1420 +
420)/2
=
1840/2 = 920.
Example:
An airline
has determined that 10 spare
brake cylinders will give
them stock out risk of
30%, whereas 14
will
reduce the risk to 15%
and 16 to 10%. It takes 3
months to receive items from
supplier and the airline
has an
average
of 4 cylinders per month. At
what stock level should
they reorder assuming that
they wish to maintain
an
85%
service level.
Solution:
Lead
time demand = 3 x 4 = 12
items
Safety
stock at 85% service
=
15% disservice
or
15% stock out
risk
=
14 items
Reorder
level = 12 + 14 = 26 items.
Example:
Data on
the distribution of lead
time for a motor component
were collected as shown.
Management would
like
to set safety stock levels
that will limit the
stock out to 10%.
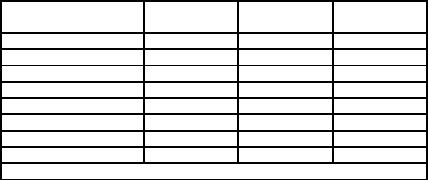
Lead
time (weeks)
1
2
3
4
5
6
7
8
Frequency
of occurrence
10
20
70
40
30
10
10
10
76
Operations
Research (MTH601)
77
How
many weeks of safety stock
are required to provide the
desired service
level?
Solution:
Lead
time (weeks)
Frequency
Probability
Cumulative
Probability
1
10
0.05
0.05
2
20
0.10
0.15
3
70
0.35
0.50
4
40
0.20
0.70
5
30
0.15
0.85
6
10
0.05
0.90
7
10
0.05
0.95
8
10
0.05
1.00
200
Average
lead time = ∑
(lead
time x frequency)/ ∑
frequency
=
(10 + 40 + 210 + 160 + 150 +
60 + 70 + 80)/200
=
770/200 = 3.85 weeks
Upto
90% service level max.
lead time is 6 weeks.
Hence
6 - 3.85 = 2.15 weeks of
stock would provide the
service level of 90%
(Note:
If the lead time is given as
a continuous time distribution
take the mid
point.)
Example:
Demand for
a product during an order
period is assumed to be normally
distributed with mean of
1000
units
and standard deviation of 40
units. What % service can a
company expect to provide
(i) if it satisfies
the
average
demand only (ii) if it
carries a safety stock of 60
units.
Solution:
1.
If
the company provides only
average demand, we can
expect only 50% service
level.
2.
The
standard normal variate Z is
computed with the following
formula.
Z
= (Safety stock - 0)/
Standard deviation
=
(60 - 0)/40 = 1.5
The
area under normal curve
for Z = 1.5 is
0.4332.
∴
Service
level = 0.50 + 0.4332 =
0.9332
04
93.32%
Example:
A manufacturer of
water filters purchases
components in EOQ's of 850
units/order. Total
demand
averages
12000 components per year
and MAD = 32 units per
month. If the manufacturer
carries a safety stock of
80
units,
what service level does
the this give the
firm?
Solution:
77
Operations
Research (MTH601)
78
2
×
MAD
=
MAD
/
0.8 =
32 /
0.8 =
40
Standard
deviation =
š
Z
= (S S - 0)/S.D = (80 - 0)/40 =
2
The
area under normal curve
for Z = 2 = 0.4772.
Service
level = 0.9772 or
97.72%
Example:
A firm has
normally distributed forecast of
usage with MAD = 60 units. It
desires a service level,
which
limits
the stock, outs to one
order cycle per
year.
(1)
How much safety stock
should be carried if the
order quantity is normally a
week's supply?
(2)
How much safety stock
should be carried if the
order quantity is weeks
supply.
Solution:
No.
of orders = 52/year.
1
stock out in 52 weeks means
a 98 % = (51/52) values
For
98% area, the value
of
Z
= 2.05 (from tables)
S
D = MAD/0.8 = 60/08
Z
= (S S - 0 )/S D= (S S - 0)/60/0.8
2.05
= (S S - 0 ) x 0.8/60
SS
= 2.05 x 60/0.8 = 154
units.
(a)
Number of orders =
52/5
1
stock out = (52/5 -
1)
Service
level = (47/5)/(52/5) = 47/52 =
0.904
Z
= 1.285 (for area = 0.404)
MAD = 60
1.285
= S S/75
S
S = 75 x 1.285 = 96 units.
78
Table of Contents:
- Introduction:OR APPROACH TO PROBLEM SOLVING, Observation
- Introduction:Model Solution, Implementation of Results
- Introduction:USES OF OPERATIONS RESEARCH, Marketing, Personnel
- PERT / CPM:CONCEPT OF NETWORK, RULES FOR CONSTRUCTION OF NETWORK
- PERT / CPM:DUMMY ACTIVITIES, TO FIND THE CRITICAL PATH
- PERT / CPM:ALGORITHM FOR CRITICAL PATH, Free Slack
- PERT / CPM:Expected length of a critical path, Expected time and Critical path
- PERT / CPM:Expected time and Critical path
- PERT / CPM:RESOURCE SCHEDULING IN NETWORK
- PERT / CPM:Exercises
- Inventory Control:INVENTORY COSTS, INVENTORY MODELS (E.O.Q. MODELS)
- Inventory Control:Purchasing model with shortages
- Inventory Control:Manufacturing model with no shortages
- Inventory Control:Manufacturing model with shortages
- Inventory Control:ORDER QUANTITY WITH PRICE-BREAK
- Inventory Control:SOME DEFINITIONS, Computation of Safety Stock
- Linear Programming:Formulation of the Linear Programming Problem
- Linear Programming:Formulation of the Linear Programming Problem, Decision Variables
- Linear Programming:Model Constraints, Ingredients Mixing
- Linear Programming:VITAMIN CONTRIBUTION, Decision Variables
- Linear Programming:LINEAR PROGRAMMING PROBLEM
- Linear Programming:LIMITATIONS OF LINEAR PROGRAMMING
- Linear Programming:SOLUTION TO LINEAR PROGRAMMING PROBLEMS
- Linear Programming:SIMPLEX METHOD, Simplex Procedure
- Linear Programming:PRESENTATION IN TABULAR FORM - (SIMPLEX TABLE)
- Linear Programming:ARTIFICIAL VARIABLE TECHNIQUE
- Linear Programming:The Two Phase Method, First Iteration
- Linear Programming:VARIANTS OF THE SIMPLEX METHOD
- Linear Programming:Tie for the Leaving Basic Variable (Degeneracy)
- Linear Programming:Multiple or Alternative optimal Solutions
- Transportation Problems:TRANSPORTATION MODEL, Distribution centers
- Transportation Problems:FINDING AN INITIAL BASIC FEASIBLE SOLUTION
- Transportation Problems:MOVING TOWARDS OPTIMALITY
- Transportation Problems:DEGENERACY, Destination
- Transportation Problems:REVIEW QUESTIONS
- Assignment Problems:MATHEMATICAL FORMULATION OF THE PROBLEM
- Assignment Problems:SOLUTION OF AN ASSIGNMENT PROBLEM
- Queuing Theory:DEFINITION OF TERMS IN QUEUEING MODEL
- Queuing Theory:SINGLE-CHANNEL INFINITE-POPULATION MODEL
- Replacement Models:REPLACEMENT OF ITEMS WITH GRADUAL DETERIORATION
- Replacement Models:ITEMS DETERIORATING WITH TIME VALUE OF MONEY
- Dynamic Programming:FEATURES CHARECTERIZING DYNAMIC PROGRAMMING PROBLEMS
- Dynamic Programming:Analysis of the Result, One Stage Problem
- Miscellaneous:SEQUENCING, PROCESSING n JOBS THROUGH TWO MACHINES
- Miscellaneous:METHODS OF INTEGER PROGRAMMING SOLUTION