IMPLEMENTATION OF AN ODD-PARITY GENERATOR CIRCUIT

<< ODD-PRIME NUMBER DETECTOR, Combinational Circuit Implementation

BCD ADDER: 2-digit BCD Adder, A 4-bit Adder Subtracter Unit >>

CS302 - Digital Logic & Design

Lesson No. 14

IMPLEMENTATION OF AN ODD-PARITY GENERATOR CIRCUIT

The first step in implementing any circuit is to represent its operation in terms of a Truth

or Function table. The function table for an 8-bit data as input has 28 has 256 input

combinations, which becomes unmanageable. Therefore, for the sake of simplicity a 4-bit data

with odd parity is assumed. The receiver circuit is also based on the 4-bit data. The function

table for the 4-bit data is shown. Figure 14.1

Input

Output

Input

Output

Table 14.1

Function Table of an Odd-Parity Generator Circuit

The function table represents the 16 possible combinations of 4 data bits. The 4 data

bits are represented by variables D3, D2, D1 and D0. The output P represents the state of the

Parity bit. Since Odd-Parity is being used therefore the 4-bit data and the parity bit should add

up to give odd number of 1s. The function table shows the Parity bit set to 1 when the 16, 4-bit

data input combinations have no 1s or an even number of 1s.

The information in the function table is mapped directly to a four variable K-map to

simplify the Boolean expression represented by the Odd-Parity generator function. None of the

1s mapped in the K-map are adjacent to each other thus the function mapped to the K-map

can not be simplified. Figure 14.1

D3D2\D1D0

Figure 14.1

Karnaugh map of the Odd-Parity Generator Function

However, using the Rules of Boolean algebra, applying Demorgan's theorems and

knowing the function table of XOR and XNOR gates the Boolean expression can be simplified.

Simplifying the expression based on SOP form results in

ABCD + ABCD + ABCD + ABCD + ABCD + ABCD + ABCD + ABCD

= AB(CD + CD) + AB(CD + CD) + AB(CD + CD) + AB(CD + CD)

= (CD + CD)(AB + AB) + (CD + CD)(AB + AB)

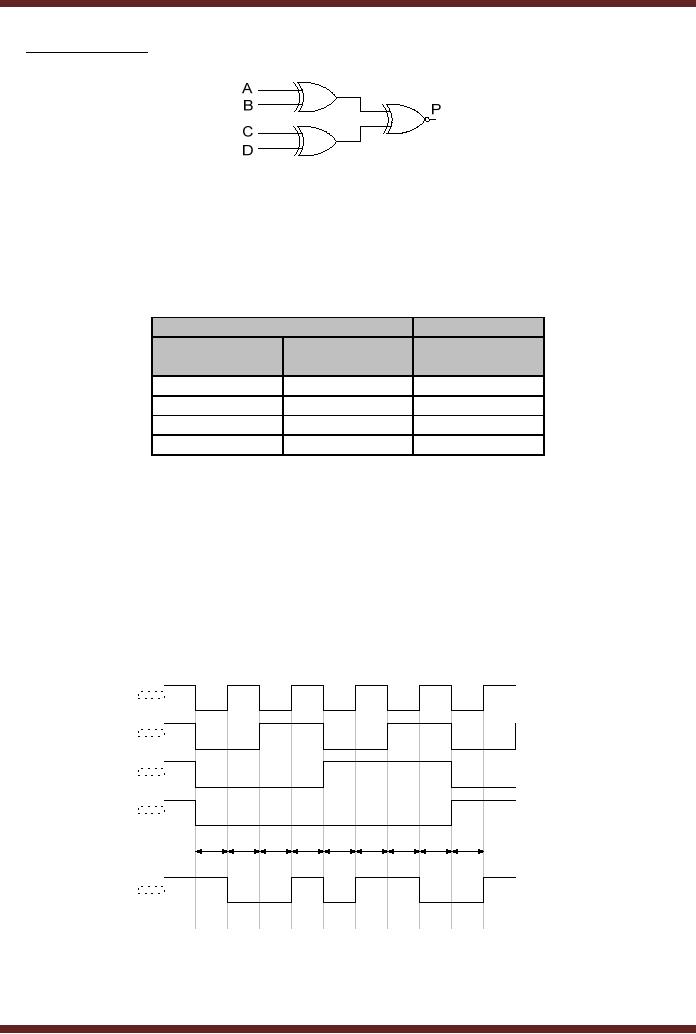
= (C ⊕ D)(A ⊕ B) + (C ⊕ D)(A ⊕ B)

131

CS302 - Digital Logic & Design

= (A ⊕ B) ⊕ (C ⊕ D)

Figure 14.2

Odd-Parity Generator Circuit

The parity generator circuit shown checks the 4-bit number, generates a parity bit

which along with the 4-bit data is transmitted. The receiver calculates the parity bit of the

received 4-bit data and compares it with the parity sent. If the received and calculated parity

bits are the same, then no error has occurred. An XOR gate is used to detect parity errors.

Table 14.2

Input

Output

Received

Calculated

Error Output

Parity Bit

Table 14.2

Detecting Error at Receiver End

Operation of Odd-Parity Generator Circuit

The timing diagram shows the operation of the Odd-Parity generator circuit. Figure

14.3. The A, B, C and D timing diagrams represent the changing 4-bit data values. During time

interval t0 the 4-bit data value is 0000, during time interval t1, the data value changes to 0001.

Similarly during time intervals t2, t3, t4 up to t8 the data values change to 0010, 0011, 0100

and 1000 respectively. During interval t0 the output of the two XOR gates is 0 and 0, therefore

the output of the XNOR gate is 1. At interval t1, the outputs of the two XOR gates is 1 and 0,

therefore the output of the XNOR gate is 0. The output P can similarly be traced for intervals t2

to t8.

Figure 14.3

Timing Diagram of Odd-Parity Generator Circuit

132

CS302 - Digital Logic & Design

XOR and XNOR Gates

XOR and XNOR gates are used to implement the Odd-Parity Generator Circuit. An

XNOR is also used to check for single bit errors at the Receiver end. Both, the XOR and

XNOR gates perform simple comparison functions. The XOR gate detects dissimilar inputs,

where as the XNOR gate looks for similar inputs. Both, the gates can be considered as

functional devices as each gate performs a simple specific function.

The XOR and XNOR gates are implemented using a combination of NOT, AND and

OR gates. Since the function performed by the XOR and XNOR gate is commonly used in

digital circuits therefore XOR and XNOR gates are available in Integrated circuit form which

can be readily used instead of implementing an XOR and XNOR circuit based on NOT-AND-

OR combination of gates.

The function table for the Parity Error detector circuit is identical to the truth table of an

XOR gate. Boolean expression representing the function of an XOR gate is AB + AB which is

implemented using a combination NOT, AND and OR gates.

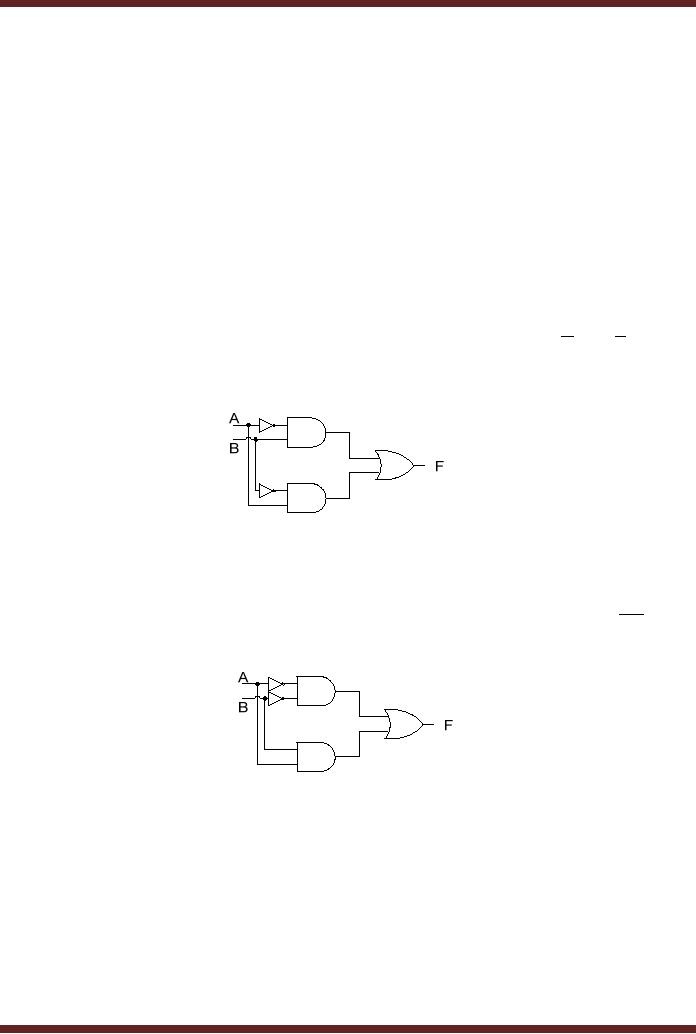
Figure 14.3

Implementation of XOR Gate

The XNOR gate is also implemented using a combination of NOT, AND and OR gates.

The function of the XNOR gate is represented in term of Boolean expression as AB + AB .

Figure 14.4

Implementation of XNOR Gate

Combinational Function Devices

Digital circuits are formed by the combination of Logic Gates. Most Combinational

circuits perform standard and useful functions such as addition, comparison, decoding and

encoding, multiplexing and de-multiplexing, selection and enabling of devices and many more

operations. Implementation of these standard functional devices through combination of gates

takes up considerable space, therefore these functional devices are implemented as MSI or

Medium Scale Integrated Chips.

133

CS302 - Digital Logic & Design

The simplest of these functional devices can be considered to be the NAND and NOR

gates which perform the AND-NOT and OR-NOT functions. The XOR and XNOR Gates are

also a combination of NOT-AND-OR gates which perform functions to detect dissimilar and

similar inputs.

Half Adder and Full Adder

A single bit binary adder circuit basically adds two bits and a carry bit, generated by the

addition of the least significant bits. The output of the single bit adder circuit generates a sum

bit and a carry bit. A single digit binary adder circuit therefore has three inputs, one

representing single bit number A, the other representing the single bit number B and the third

bit represents the single bit carry. The single bit binary adder has two bit output. One bit

represents the Sum between numbers A and B. The other bit represents the carry bit

generated due to addition.

In Digital logic terminology the adder which has been described is known as a full

adder. An adder circuit that only has two bit input representing the two single bit numbers A

and B and does not have the carry bit input from the least significant digit is regarded as a

half-adder. The block diagrams represent a Half-Adder and a Full-Adder. Figure 14.5.

1. Half-Adder

A Half-Adder can be fully described in terms of its Function table, its Sum and Carry

Out Boolean Expressions and the circuit Implementation.

∑

Cout

Cin

Half-Adder

Full-Adder

Figure 14.5

Block diagrams of Half-Adder and Full-Adder

Half-Adder Function Table

The Half-Adder has a 2-bit input and a 2-bit output. The function table of the Half-Adder

has two input columns representing the two single bit numbers A and B. The function table

also has two output columns representing the Sum bit and Carry Out bit. Table 14.3

Input

Output

Sum

Carry Out

Table 14.3

Half-Adder Function Table

134

CS302 - Digital Logic & Design

Half-Adder Sum & Carry Out Boolean Expressions

The Sum and Carry Out expressions of the Half-Adder can be determined from the

function table. The Half-Adder Sum and Carry Out outputs are defined by the expressions

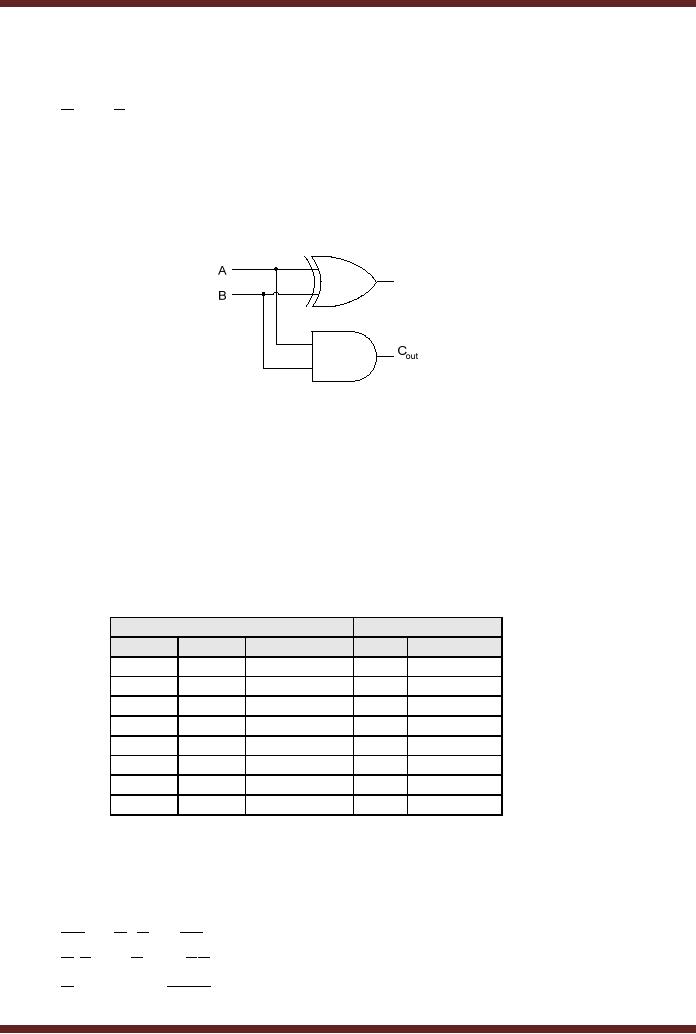
Sum = AB + AB = A ⊕ B

CarryOut = AB

Half-Adder Logic Circuit

The Half-Adder Logic Circuit can be directly implemented from the Sum and Carry Out

Boolean expressions. Figure 14.6

∑

Figure 14.6

Half-Adder Logic Circuit

2. Full-Adder

A Full-Adder can be fully described in terms of its Function table, its Sum and Carry

Out Boolean Expressions and the circuit Implementation.

Full-Adder Function Table

The Full-Adder has a 3-bit input and a 2-bit output. The function table of the Full-Adder

has three input columns representing the two single bit numbers A, B and the Carry In bit. The

function table also has two output columns representing the Sum bit and Carry Out bit. Table

14.4

Input

Output

Carry In(C)

Sum Carry Out

Table 14.4

Full-Adder Function Table

Full-Adder Sum & Carry Out Boolean Expressions

The Sum and Carry Out expressions of the Full-Adder can be determined from the

function table. The Full-Adder Sum and Carry Out outputs are defined by the expressions

Sum = ABC + ABC + ABC + ABC

Sum = A(BC + BC) + A(BC + BC)

Sum = A(B ⊕ C) + A(B ⊕ C)

135

CS302 - Digital Logic & Design

Sum = A ⊕ B ⊕ C

CarryOut = ABC + ABC + ABC + ABC

CarryOut = C(AB + AB) + AB(C + C)

CarryOut = C(A ⊕ B) + AB

Full-Adder Logic Circuit

The Full-Adder Logic Circuit can be directly implemented from the Sum and Carry Out

Boolean expressions. Figure 14.7

∑

Cin

Cout

Figure 14.7

Full-Adder Logic Circuit

Forming a Full-Adder using Half-Adders

A 1-bit Full-Adder cane be implemented by combining together two Half-Adders. Figure

14.8

∑

Figure14.8

Implementing a Full-Adder using two Half-Adders

The Sum output of the first Half-Adder is (A ⊕ B)

The Carry Out of the first Half-Adder is AB

The Sum output of the second Half-Adder is (A ⊕ B) ⊕ Cin = (A ⊕ B ⊕ Cin )

136

CS302 - Digital Logic & Design

The Carry Out of the second Half-Adder is (A ⊕ B)Cin

The output of the OR gate is AB + (A ⊕ B)Cin

Parallel Binary Adders

Single bit Full or Half Adders do not perform any useful function. To add two 4-bit

numbers a 4-bit adder is required. Four single bit Full-Adders are connected together to form a

4-bit Parallel Adder capable of adding two 4-bit binary numbers. Figure 14.9.

The two 4-bit numbers A and B are applied at the circuit inputs A0-3 and B0-3

respectively. The 4-bit Sum output of the Parallel Adder is available at outputs S0-3. The Carry

In to the circuit is set to 0. (Cin=0). The Carry is available at Cout.

Figure 14.9

4-bit Parallel Binary Adder

Carry Propagation

Parallel Binary Adders can be implemented by connecting the required number of 1-bit

full adders in a configuration represented in figure 14.9. However, there is a practical limitation

to the number of 1-bit Full-Adders that can be connected in parallel. In the 4-bit Parallel Adder,

the Most significant bit adder which adds bits A3, B3 and the Carry bit C3, can not proceed until

it receives the Carry from the next least significant 1-bit adder which adds bits A2, B2. The A2

B2 bit adder can not proceed unless it receives the carry input C2 from the A1, B1 adder. The

A1, B1 adder in tern depends on A0, B0 adder to provide the carry input. Thus the carry has to

propagate through each Full-adder before it reaches the last or most significant full adder.

Assume that each gate has a propagation delay of 10 nsec. A 1-bit Full Adder

generates a Carry out after 30 nsec. For a 4-bit Parallel Adder Full-adder the Carry out from

the most significant adder would be after 120 nsec. The delay can increase to prohibitive

levels if 8-bit, 16-bit or 64-bit parallel adders are implemented. 64-bit parallel adders are used

by computers.

Look-Ahead Carry Circuits

To overcome the problem of carry propagation or carry ripple, Look-Ahead carry

generator circuits are used. These circuits look at the bits to be added and decide if a higher

order carry is to be generated. The Look-Ahead Carry Circuits although increase the circuitry

but they provide a practical solution to the prohibitive delays that are caused by the ripple carry

in parallel adders.

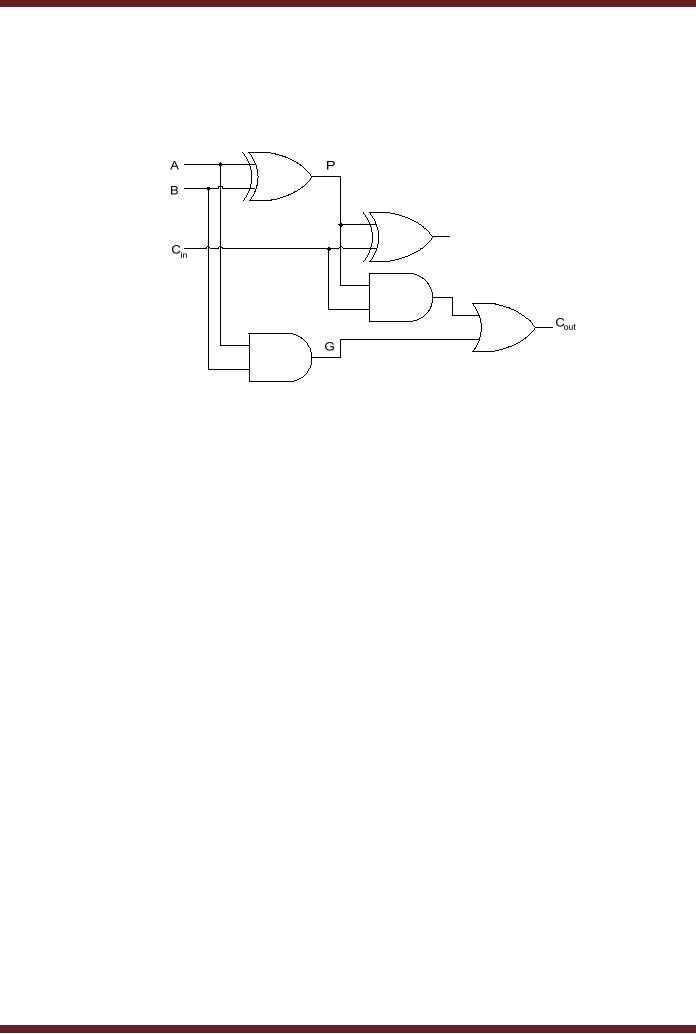
Consider the Full-Adder Circuit. 14.10. The output (A ⊕ B) at output P of the XOR gate

and the output AB at output G of the AND gate is available simultaneously after one gate

delay. If the G output of the AND gate is 1, the Carry Out has to be a 1 no matter what is the

137

CS302 - Digital Logic & Design

other input of the Carry Out OR gate. The Sum and Carry Out can be expressed in terms of P

and G gate outputs.

· The P output is called the Carry Propagate.

· The G output is called the Carry Generate

∑

Figure 14.10 Full-Adder with Carry Generate and Carry Propagate

Carry Outputs in terms of Carry Propagate and Carry Generate

The Sum and Carry Out Boolean expressions can be rewritten in terms of P, Carry

Propagate and G, Carry Generate terms.

Sum = P ⊕ C

CarryOut = CP + G

Writing the expressions for the four Carry Out terms C1, C2, C3 and C4 in terms of Carry

Propagate P and Carry Generate G.

C1 = C 0P0 + G0

· C 2 = C1P1 + G1 = P1 (C 0P0 + G0 ) + G1 = G1 + P1G0 + P0P1C 0

· C3 = G 2 + P2G1 + P1P2G0 + P0P1P2C0

· C3 = C 2P2 + G 2 = P2 (G1 + P1G0 + P0P1C 0 ) + G 2 = G 2 + P2G1 + P1P2G0 + P0P1P2C 0

· C 4 = G3 + P3G 2 + P2P3G1 + P1P2P3G0 + P0P1P2P3C 0

where Pn = A n ⊕ Bn and Gn = A nBn

The Look-Ahead Carry Generator Circuit is shown. Figure 14.11. The inputs to the

Look-Ahead Carry Generator Circuit are the Carry Propagate terms P0, P1, P2 and P3 and Carry

Generate terms G0, G1, G2 and G3.

The Carry Propagate P0, P1, P2 and P3 and Carry Generate terms G1, G2, G3 and G4

are generated by the XOR and AND gates after one gate delay.

The Outputs of the Look-Ahead Carry Generator Circuit are C1, C2, C3 and C4. The

output C1 is generated by the circuit represented by the expression C1 = C 0P0 + G0 which

138

CS302 - Digital Logic & Design

requires an AND gate to generate the product term C 0P0 and a second level two input OR

gate to sum the terms C 0P0 and G0 . Thus C1 is available after two gate delays.

Look-Ahead

Carry

Generator

Figure 14.11 Look-Ahead Carry Generator

Similarly, the output C2 is generated by the circuit represented by the expression

C 2 = G1 + P1G0 + P0P1C 0 which requires a 2-input and 3-input AND gates to generate the

product terms P1G0 and P0P1C 0 respectively. A second level three input OR gate is required to

sum the three terms. Thus C2 is also available after two gate delays.

The output C3 is

generated by the circuit represented by

the

expression C3 = G 2 + P2G1 + P1P2G0 + P0P1P2C0 . The expression is implemented by a

combination of three AND gates having 2, 3 and 4 inputs respectively and a single 4-input OR

gate. Again two levels of gates is used, C3 is available after a gate delay of two.

Finally, the output C4 is generated by the circuit represented by the

expression C 4 = G3 + P3G 2 + P2P3G1 + P1P2P3G0 + P0P1P2P3C 0 . To implement the expression

two levels of 2, 3, 4 and 5 input AND gates and a single 5 input OR gate is used. C4 is

available after a gate delay of two.

Thus for Carry outputs C1, C2, C3 and C4 the delay is of the order of two after the

Propagate Carry and Generate Carry terms become available.

139

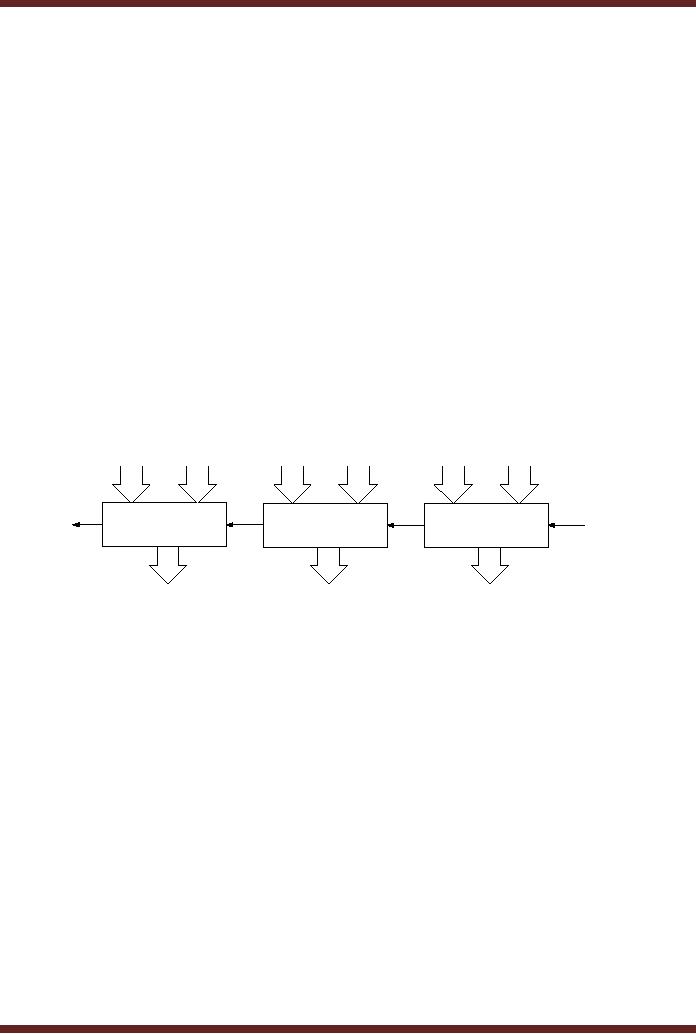
CS302 - Digital Logic & Design

MSI Adders

4-bit parallel Adders are available as Medium Scale Integrated Circuits. These circuits

use the Look-Ahead Carry Circuitry to remove the carry ripple. The two ICS are 74LS83A and

74LS283. Both the devices are functionally identical, however they are not pin compatible.

These devices are packaged as 16-pin devices. The division of the 16 pins is

· 4 pins for the 4-bit input A

· 4 pins for the 4-bit input B

· 4 pins for the 4-bit output Sum

· 1 pin for Carry In

· 1 pin for Carry Out

· 1 pin for Circuit Power Supply

· 1 pin for Circuit GND

The 74LS83A or the 74LS283 can be cascaded together to form 8-bit, 12-bit or 16-bit

Parallel Adders. Figure 14.12 The Carry Out pin of one IC is connected to the Carry In pin of

the other IC.

A (4-7)

A (0-3)

A (8-11)

B (8-11)

B (4-7)

B (0-3)

C12

C0=0

74LS283

Sum (8-11)

Sum (4-7)

Sum (0-3)

Figure 14.12

12-bit Parallel Adder using three 74LS283 ICs

140

Table of Contents: