 |

Database
Management System
(CS403)
VU
Lecture No.
19
Reading
Material
"Database
Systems Principles, Design
and Implementation"
Section
7.1 7.7
written
by Catherine Ricardo, Maxwell
Macmillan.
"Database
Management Systems", 2nd edition, Raghu Ramakrishnan,
Johannes Gehrke,
McGraw-Hill
Overview of Lecture:
o Functional
Dependency
o Inference
Rules
o Normal
Forms
In the
previous lecture we have
studied different types of
joins, which are used
to
connect
two different tables and
give different output
relations. We also started the
basics of
normalization. From this
lecture we will study in length
different aspects of
normalization.
Functional
Dependency
Normalization
is based on the concept of functional
dependency. A functional
dependency
is a type of relationship between
attributes.
164

Database
Management System
(CS403)
VU
Definition
of Functional Dependency
If A
and B are attributes or sets
of attributes of relation R, we say
that B is
functionally
dependent on A if each value of A in R
has associated with it
exactly one
value of
B in R.
We write
this as A
B, read as "A
functionally determines B" or " A
determines B".
This
does not mean that A causes
B or that the value of B can
be calculated from
the
value of
A by a formula, although sometimes that
is the case. It simply means
that if
we know
the value of A and we
examine the table of
relation R, we will find only
one
value of
B in all the rows that
have the given value of A at
any one time. Thus
then
the
two rows have the
same A value, they must also
have the same B value.
However,
for a
given B value, there may be
several different A values.
When a functional
dependency
exits, the attributes or set
of attributes on the left
side of the arrow is
called a
determinant. Attribute of set of
attributes on left side are
called determinant
and on
right are called dependants. If
there is a relation R with
attributes (a,b,c,d,e)
a
b,c,d
d
e
For
Example there is a relation of
student with following
attributes. We will establish
the
functional dependency of different
attributes: -
STD
(stId,stName,stAdr,prName,credits)
stId
stName,stAdr,prName,credits
prName
credits
Now in
this example if we know the
stID we can tell the
complete information
about
that
student. Similarly if we know
the prName , we can tell
the credit hours for
any
particular
subject.
Functional
Dependencies and
Keys:
We can
determine the keys of a
relation after seeing its
functional dependencies. The
determinant
of functional dependency that
determines all attributes of
that table is the
super
key. Super key is an
attribute or a set of attributes
that identifies an
entity
uniquely.
In a table, a super key is any
column or set of columns whose
values can be
used to
distinguish one row from
another. A minimal super key
is the candidate key
,
so if a
determinant of functional dependency
determines all attributes of
that relation
then it
is definitely a super key and if
there is no other functional
dependency whereas
a subset
of this determinant is a super key
then it is a candidate key. So
the functional
dependencies
help to identify keys. We
have an example as under:
-
EMP
(eId,eName,eAdr,eDept,prId,prSal)
eId
(eName,eAdr,eDept)
eId,prId
prSal
Now in
this example in the employee
relation eId is the key
from which we can
uniquely
determine the employee name
address and department .
Similarly if we
know
the employee ID and project
ID we can find the project
salary as well. So FDs
help in
finding out the keys
and their relation as
well.
165

Database
Management System
(CS403)
VU
Inference
Rules
Rules of
Inference for functional dependencies,
called inference axioms or
Armstrong
axioms,
after their developer, can
be used to find all the FDs
logically implied by a
set
of FDs.These
rules are sound , meaning
that they are an immediate
consequence of
the
definition of functional dependency
and that any FD that
can be derived from a
given
set of FDs using them is
true. They are also
complete, meaning they can
be used
to derive
every valid reference about
dependencies .Let A,B,C and D be
subsets of
attributes
of a relation R then following
are the different inference
rules: -
Reflexivity:
If B is a
subset of A, then A
B. This
also implies that A
A always
holds.
Functional
dependencies of this type are called
trivial dependencies. For
Example
StName,stAdr
stName
stName
stName
Augmentation:
If we
have A
B then
AC.
BC.
For Example
If
stId
stName
then
StId,stAdr
stName,stadr
Transitivity:
If
A
B and
B
C, then
A
C
If
stId
prName
and prName
credits
then
stId
credits
Additivity
or Union:
If
A
B and
A
C, then
A
BC
If
empId
eName
and empId
qual
Then we can write it
as
empId
qual
Projectivity
or Decomposition
If
A
BC then
A
B and
A
C
If
empId
eName,qual
Then we can write it
as
empId
eName
and empID
qual
Pseudo
transitivity:
If
A
B and
CB
D, then
AC
D
If
stID
stName
and stName,fName
stAdr
Then we can write it
as
StId,fName
stAdr
Normal
Forms
Normalization
is basically; a process of efficiently
organizing data in a
database.
There
are two goals of the
normalization process: eliminate
redundant data (for
example,
storing the same data in
more than one table)
and ensure data dependencies
make
sense (only storing related
data in a table). Both of these
are worthy goals as
they
reduce the amount of space a
database consumes and ensure
that data is logically
stored.
We will now study the first
normal form
166
Database
Management System
(CS403)
VU
First
Normal Form:
A
relation is in first normal
form if and only if every
attribute is single valued
for each
tuple.
This means that each
attribute in each row , or
each cell of the table,
contains
only
one value. No repeating
fields or groups are
allowed. An alternative way
of
describing
first normal form is to say
that the domains of
attributes of a relation
are
atomic,
that is they consist of single
units that cannot be broken
down further. There
is no
multivalued (repeating group) in
the relation multiple values
create problems in
performing
operations like select or
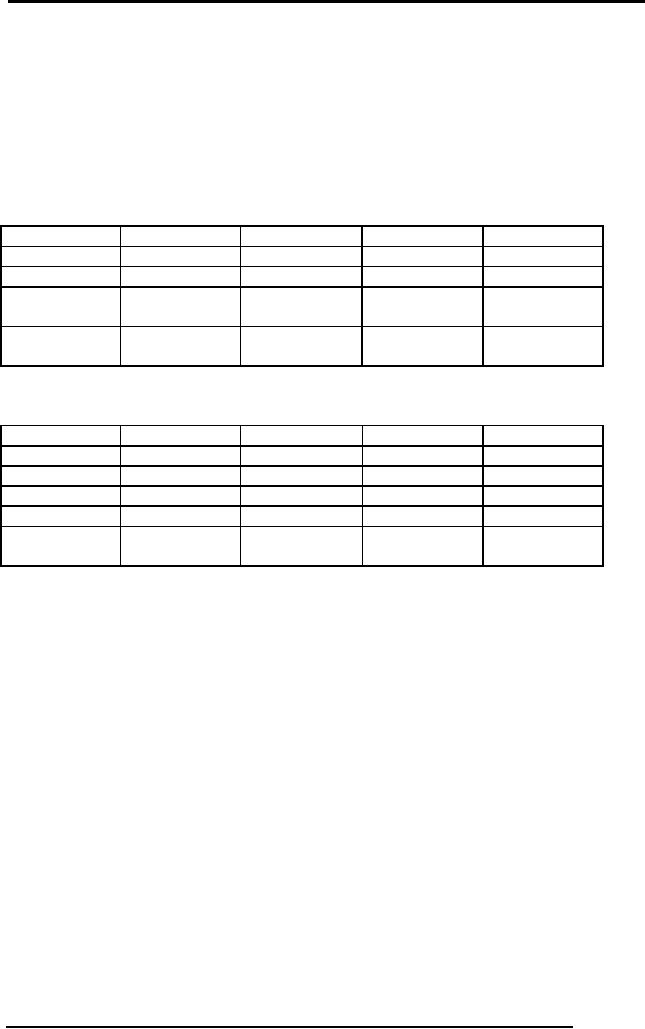
join. For Example there is a
relation of Student
STD(stIdstName,stAdr,prName,bkId)
stId
stName
stAdr
prName
bkId
S1020
Sohail
Dar
I-8
Islamabad
MCS
B00129
S1038
Shoaib
Ali
G-6
Islamabad
BCS
B00327
S1015
Tahira
Ejaz
L Rukh
Wah
MCS
B08945,
B06352
S1018
Arif
Zia
E-8,
BIT
B08474
Islamabad.
Now in
this table there is no
unique value for every
tuple, like for S1015
there are two
values
for bookId. So to bring it in
the first normal
form.
stId
stName
stAdr
prName
bkId
S1020
Sohail
Dar
I-8
Islamabad
MCS
B00129
S1038
Shoaib
Ali
G-6
Islamabad BCS
B00327
S1015
Tahira
Ejaz
L Rukh
Wah
MCS
B08945
S1015
Tahira
Ejaz
L Rukh
Wah
MCS
B06352
S1018
Arif
Zia
E-8,
BIT
B08474
Islamabad.
Now
this table is in first
normal form and for
every tuple there is a
unique value.
Second
Normal Form:
A
relation is in second normal
form (2NF) if and only if it
is in first normal form
and
all
the nonkey attributes are
fully functionally dependent on
the key. Clearly, if
a
relation
is in 1NF and the key
consists of a single attribute,
the relation is
automatically
in 2NF. The only time we
have to be concerned about 2NF is
when the
key is
composite. Second normal form
(2NF) addresses the concept of
removing
duplicative
data. It remove subsets of data
that apply to multiple rows
of a table and
place
them in separate tables. It
creates relationships between
these new tables and
their
predecessors through the use
of foreign keys.
Summary
Normalization
is the process of structuring
relational database schema
such that most
ambiguity
is removed. The stages of
normalization are referred to as
normal forms
and
progress from the least restrictive
(First Normal Form) through
the most
restrictive
(Fifth Normal Form).
Generally, most database designers do not
attempt to
implement
anything higher than Third
Normal Form or Boyce-Codd
Normal Form.
167

Database
Management System
(CS403)
VU
We have
started the process of normalization in
this lecture. We will cover
this topic
in detail
in the coming
lectures.
Exercise:
Draw
the tables of an examination
system along with attributes
and bring those
relations
in First Normal Form.
168
Table of Contents:
- Introduction to Databases and Traditional File Processing Systems
- Advantages, Cost, Importance, Levels, Users of Database Systems
- Database Architecture: Level, Schema, Model, Conceptual or Logical View:
- Internal or Physical View of Schema, Data Independence, Funct ions of DBMS
- Database Development Process, Tools, Data Flow Diagrams, Types of DFD
- Data Flow Diagram, Data Dictionary, Database Design, Data Model
- Entity-Relationship Data Model, Classification of entity types, Attributes
- Attributes, The Keys
- Relationships:Types of Relationships in databases
- Dependencies, Enhancements in E-R Data Model. Super-type and Subtypes
- Inheritance Is, Super types and Subtypes, Constraints, Completeness Constraint, Disjointness Constraint, Subtype Discriminator
- Steps in the Study of system
- Conceptual, Logical Database Design, Relationships and Cardinalities in between Entities
- Relational Data Model, Mathematical Relations, Database Relations
- Database and Math Relations, Degree of a Relation
- Mapping Relationships, Binary, Unary Relationship, Data Manipulation Languages, Relational Algebra
- The Project Operator
- Types of Joins: Theta Join, Equi–Join, Natural Join, Outer Join, Semi Join
- Functional Dependency, Inference Rules, Normal Forms
- Second, Third Normal Form, Boyce - Codd Normal Form, Higher Normal Forms
- Normalization Summary, Example, Physical Database Design
- Physical Database Design: DESIGNING FIELDS, CODING AND COMPRESSION TECHNIQUES
- Physical Record and De-normalization, Partitioning
- Vertical Partitioning, Replication, MS SQL Server
- Rules of SQL Format, Data Types in SQL Server
- Categories of SQL Commands,
- Alter Table Statement
- Select Statement, Attribute Allias
- Data Manipulation Language
- ORDER BY Clause, Functions in SQL, GROUP BY Clause, HAVING Clause, Cartesian Product
- Inner Join, Outer Join, Semi Join, Self Join, Subquery,
- Application Programs, User Interface, Forms, Tips for User Friendly Interface
- Designing Input Form, Arranging Form, Adding Command Buttons
- Data Storage Concepts, Physical Storage Media, Memory Hierarchy
- File Organizations: Hashing Algorithm, Collision Handling
- Hashing, Hash Functions, Hashed Access Characteristics, Mapping functions, Open addressing
- Index Classification
- Ordered, Dense, Sparse, Multi-Level Indices, Clustered, Non-clustered Indexes
- Views, Data Independence, Security, Vertical and Horizontal Subset of a Table
- Materialized View, Simple Views, Complex View, Dynamic Views
- Updating Multiple Tables, Transaction Management
- Transactions and Schedules, Concurrent Execution, Serializability, Lock-Based Concurrency Control, Deadlocks
- Incremental Log with Deferred, Immediate Updates, Concurrency Control
- Serial Execution, Serializability, Locking, Inconsistent Analysis
- Locking Idea, DeadLock Handling, Deadlock Resolution, Timestamping rules