 |
Equivalent FAs |
| << Finite Automaton |
| FA corresponding to finite languages >> |
Theory of
Automata
(CS402)
Theory of
Automata
Lecture
N0. 6
Reading
Material
Chapter
5
Introduction
to Computer Theory
Summary
Language
of strings beginning with
and ending in different
letters, Accepting all
strings, accepting
non-
empty
strings, accepting no string,
containing double a's,
having double 0's or double
1's, containing
triple
a's or triple b's,
EVEN-EVEN
Example
Consider
the Language L of Strings, defined
over Σ = {a, b}, beginning
with and ending in different
letters.
The
language L may be expressed by
the following regular
expression a(a + b)*b + b(a +
b)*a
This
language may be accepted by
the following FA a
b
b
4+
2
a
a
1
b
a
a
b
5+
3
b
Example
Consider
the Language L, defined over Σ =
{a, b} of all
strings including Λ. The
language L may be
accepted
a,b
by the
following FA
a,b
1±
2+
The
language L may also be
accepted by the following
FA
a,b
±
The
language L may be expressed by
the regular expression (a +
b)*
Example
Consider
the Language L , defined over Σ =
{a, b} of all
non empty strings. The
language L may be
accepted
a,b
by the
following FA
a,b
-
+
The
above language may be
expressed by the regular
expression (a + b)+
Example
Consider
the following FA, defined
over Σ = {a, b}
a,b
a,b
-
+
It is to be
noted that the above FA
does
not accept any string,
even it
does not accept the null
string; as there is
no path
starting from initial state
and ending in final
state.
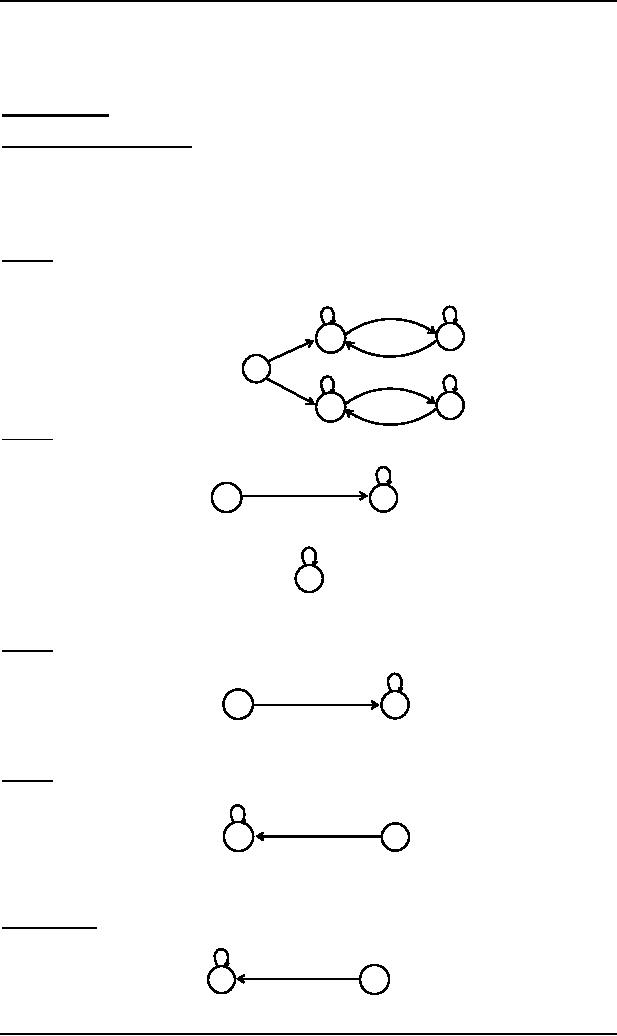
Equivalent
FAs
It is to be
noted that two FAs
are said to be equivalent, if
they accept the same
language, as shown in
the
following
FAs.
a,b
FA1
a,b
+
17
Theory of
Automata
(CS402)
a,b
a,b
1-
2
FA2
a,b
a,b
a,b
3+
1-
2
FA3
±
Note
FA1 has already been discussed,
while in FA2,
there is no final state and
in FA3, there is a final
state but FA3
is
disconnected
as the states 2 and 3 are
disconnected.
It may
also be noted that the
language of strings accepted by
FA1, FA2 and
FA3 is denoted by the
empty set i.e.
{ } OR
Ø
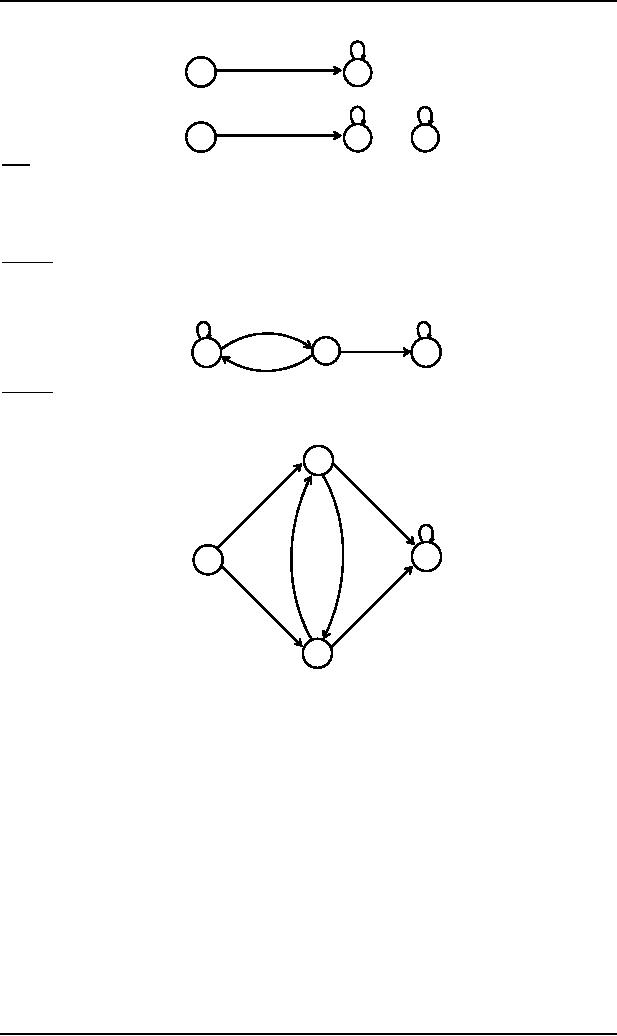
Example
Consider
the Language L of strings , defined
over Σ = {a, b}, containing
double a.
The
language L may be expressed by
the regular expression
(a+b)* (aa) (a+b)*. This language may be
accepted
by the
following FA.
b
a,b
a
a
2
1-
3+
b
Example
Consider
the language L of strings,
defined over Σ={0, 1},
having
double 0's or double 1's,
The
language L
may be
expressed by the regular
expression (0+1)* (00 +
11) (0+1)*
This
language may be accepted by
the following FA
x
0
0
0,1
1
0
+
-
1
1
y
18
Theory of
Automata
(CS402)
Example
Consider
the language L of strings,
defined over Σ={a, b},
having
triple a's or triple b's.
The
language L may
be
expressed by RE (a+b)* (aaa + bbb) (a+b)*
a
2
4
This
language may be accepted by
the FA as shown aside
a
a
a,b
b
6+
1
a
b
b
a
b
b
3
5
3
b
1±
3
b
a
a
a
a
b
4
2
b
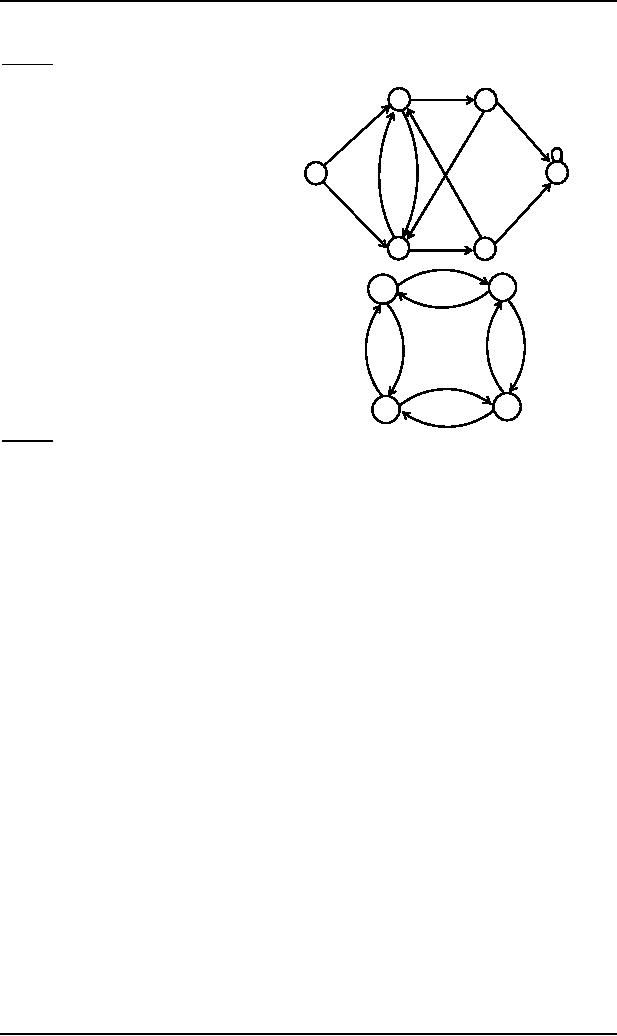
Example
Consider
the EVEN-EVEN
language,
defined over Σ = {a, b}. As
discussed earlier that EVEN-EVEN
language
can be expressed by the
regular expression (aa+bb+(ab+ba)(aa+bb)*(ab+ba))*
EVEN-EVEN
language
may be accepted by the FA as shown
aside
19
Table of Contents:
- What does automata mean, Introduction to languages
- Kleene Star Closure, Recursive definition of languages
- Regular Expression, Recursive definition of Regular Expression
- Equivalent Regular Expressions
- Finite Automaton
- Equivalent FAs
- FA corresponding to finite languages
- Examples of TGs: accepting all strings
- Generalized Transition Graphs
- Nondeterminism, Kleene’s Theorem
- Proof(Kleene’s Theorem Part II)
- Kleene’s Theorem Part III
- Concatenation of FAs
- Closure of an FA
- Nondeterministic Finite Automaton, Converting an FA to an equivalent NFA
- NFA with Null String
- NFA and Kleene’s Theorem
- NFA corresponding to Concatenation of FAs
- Distinguishable strings and Indistinguishable strings
- Finite Automaton with output, Moore machine
- Mealy machine
- Equivalent machines
- Mealy machines in terms of sequential circuit
- Regular languages, Complement of a language
- Nonregular languages
- Pumping Lemma
- Pumping Lemma version II
- Pseudo theorem
- Decidability
- finiteness of a language
- Context Free Grammar (CFG), CFG terminologies
- Trees
- Polish Notation (o-o-o)
- Total language tree, Regular Grammar
- Null Production
- Chomsky Normal Form (CNF)
- A new format for FAs
- Nondeterministic PDA
- PDA corresponding to CFG
- Conversion form of PDA
- Conversion Form, Joints of the machine
- Row language, Nonterminals
- Non-Context-Free language, Pumping lemma for CFLs
- Decidablity, Parsing Techniques
- Turing machine