DIGITAL CLOCK: Clocked Synchronous State Machines

<< Integrated Circuit Up Down Decade Counter Design and Applications

NEXT-STATE TABLE: Flip-flop Transition Table, Karnaugh Maps >>

CS302 - Digital Logic & Design

Lesson No. 30

DIGITAL CLOCK

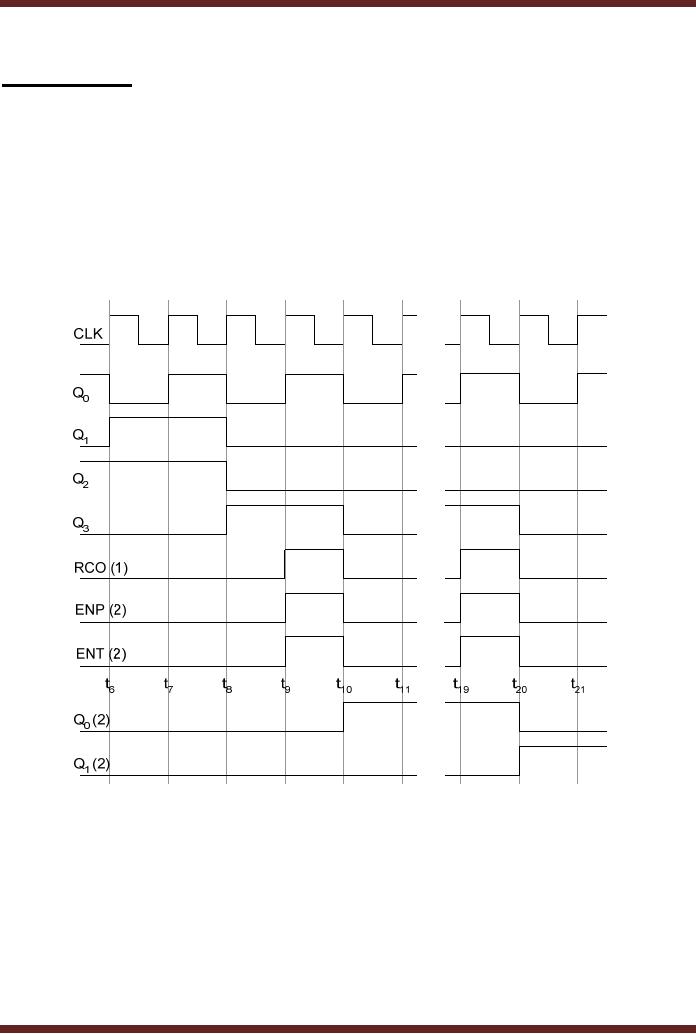
The timing diagram figure 30.1a shows the time interval t6 to t11 and t19 to t21. At time

interval t9 the units counter counts to 1001 (9) which is the terminal count of the 74x160

decade counter. The RCO signal is set to logic 1 to indicate the terminal count. The RCO

signal is connected to the ENP and ENT enable signals of the tens counter. At interval t10 the

tens counter is incremented by 1, the units counter recycles to 0000 (0) and the RCO signal is

deactivated inhibiting the tens counter from incrementing. At interval t19 the units counter once

again reaches its terminal count activating the RCO signal and enabling the tens counter to

increment its initial count 0001 to 0010. The counting sequence continues until the tens

counter increments to 0101 (5) and the units counter recycles to 0000 and continues with the

counting sequence on each positive clock transition.

Figure 30.1a Timing diagram of the divide by 60 minutes/seconds counter

The timing diagram fig 30.1b shows the timing sequence from interval t56 to t64. The unit

counter reaches its terminal count at interval t59. The output of the 3-input AND gate is set to

logic high. The output of the AND gate is connected to the ENP and ENT enable inputs of the

next counter, thus enabling the next counter. At interval t60, on a positive clock transition the

units counter recycles to 0000, the tens counter increments to 0110 (6) setting the output of

the NAND gate to logic 0 and the next counter increments its count. The NAND gate output is

connected tot the asynchronous active low clear input of the tens counter which is

asynchronously cleared to 0000.

312

CS302 - Digital Logic & Design

CLR

Figure 30.1b Timing diagram of the divide by 60 counter at time interval t56 to t64

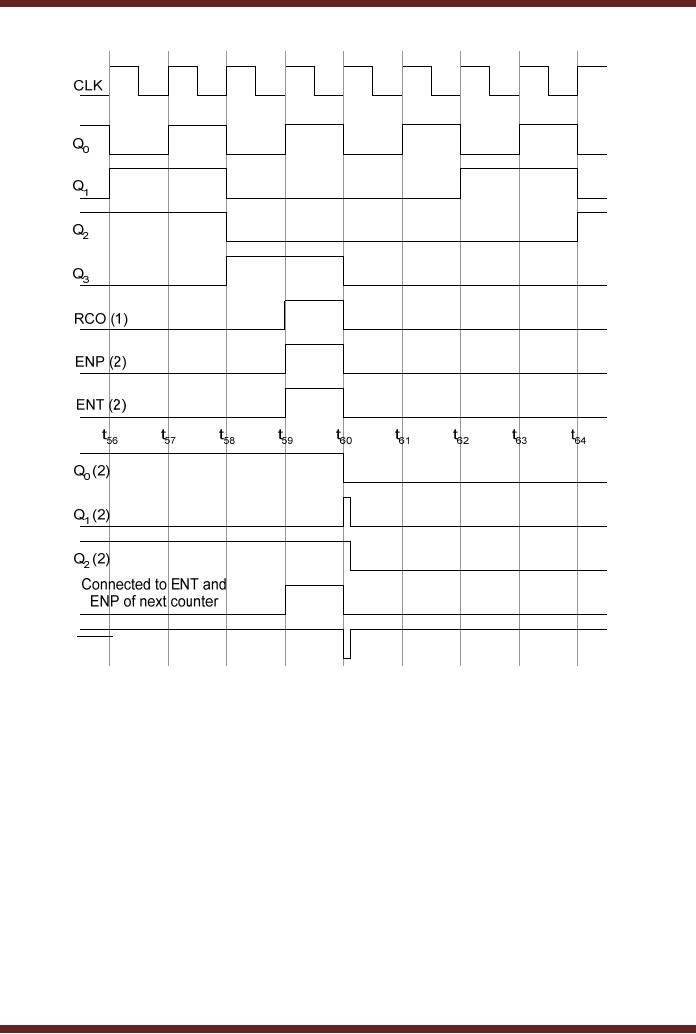
The hours unit counter circuit is configured as a decade counter, counting from 0000 to

1001 when it is enabled by the Minutes counter circuit. The NOT gate connected to the clock

input of the J-K flip-flop allows the negative-edge triggered J-K flip-flop to trigger when the

units counter is triggered to count from 0000 to 1001. The terminal count 1001 is detected by

the NAND gate (1) at interval t9 which sets the J input of the flip-flop to logic 1. The K input of

the flip-flop is at Logic 0, therefore on a clock transition at interval t10 the JK flip-flop output Q

is set to logic 1, the units counter recycles to 0000 resetting J input to logic 0. The unit counter

counts to 0001 and 0010 to represent hours 11 and 12 in interval t11 and t12 respectively. At

interval t12 as the unit counters count changes from 1011 (11) to 1100 (12), Q1 output is set to

logic 1, which sets the output of the NAND gate to logic 0 as the other input of the NAND is

already at logic 1 (Q). The NAND gate sets the K input to logic 1 and setting the active-low

LOAD signal to logic 0. At interval t13, at the positive clock transition the unit counter is

reloaded with the count 0001, the J-K flip-flop output toggles to logic 0 from logic 1. As the

units counter is reloaded with count 0001, the K input is set to logic 0. At intervals t14, t15 and

t16 the hours unit counter increments the hours count by 1.

313

CS302 - Digital Logic & Design

Figure 30.2a Hours Counter Circuit

LOAD

Figure 30.2b Hours Counter timing diagram

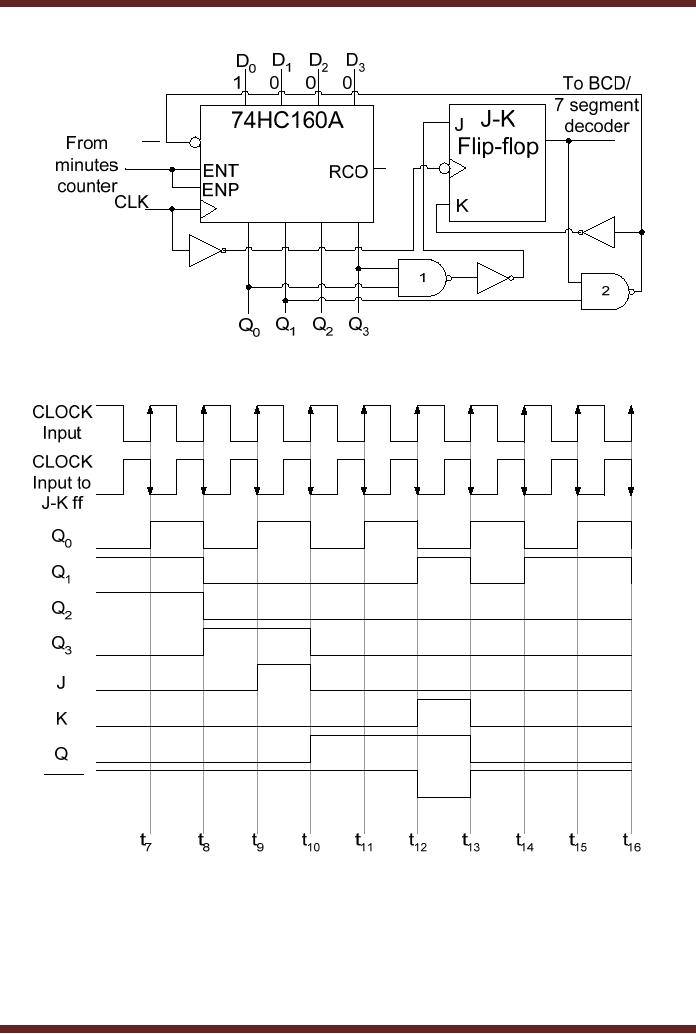
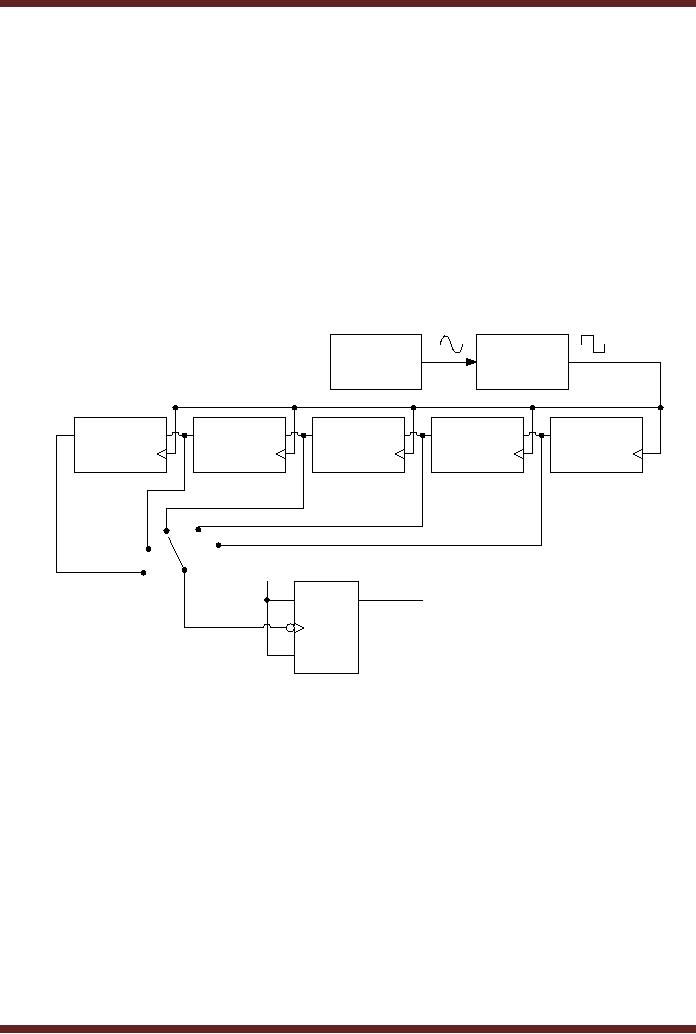
3. Frequency Counter

A frequency counter is used to measure the frequency of an input signal. The basis for

the operation of a frequency counter is counting of the clock pulses in a predetermined time

interval. The frequency of periodic signal is the number of cycles in a time period of one

second. The frequency of the unknown signal can be calculated by counting the number of

314

CS302 - Digital Logic & Design

clock pulses of the unknown signal and dividing the count number by the time interval in which

the clock pulses are counted, Figure 30.3

Clear

Input Signal with

unknown frequency

Counter

Sampling

BCD & Segment

Interval

Decoder

Figure 30.3a Frequency Counter Circuit

Input

signal

Counter

reset signal

Sampling

Interval

Counter

Input

Figure 30.3b Timing diagram of the Frequency Counter Circuit

In the circuit shown, the input signal with unknown frequency is applied at the AND

gate input. The second input of the AND gate is connected to a signal which determines the

sampling interval. The signal is set to logic high at interval t1 to enable the AND gate allowing

the input signal to be connected to the clock input of the counter circuit. The sampling interval

signal is set to logic low at the end of the sampling interval t2 to disable the AND gate and

inhibit the counter from counting. Before the counter counts the clock pulses of the input signal

315

CS302 - Digital Logic & Design

it is reset by activating the Asynchronous input to clear the counter. At the end of the sampling

interval the counter output is displayed on 7-segment displays.

The accuracy of the frequency counter depends on the duration of the timing sampling

interval, which must be very accurate. Consider that during a sampling interval of 1 second

4573 clock pulses of the input signal are measured. Thus, the frequency of the unknown signal

is 4573 Hz. If the same input signal is sampled using a 0.1 second sampling interval then

457.3 pulses are counted, which means that either 457 or 458 will be counted depending on

the start of the sampling interval at t1. Thus the frequency is determined to be either 4570 or

4580. Similarly, if the sampling interval is reduced to 0.01 seconds, the numbers of clock

pulses measured are 45.73, which means that either 45 or 46 will be read indicating a

frequency of 4500 or 4600.

100

KHz

Pulse

Crystal

Shaper

Oscillator

Div by 10

100

KHz

switch

Divide by

2 output

Figure 30.4

Cascaded Counter circuit for obtaining accurate sampling intervals

Very accurate sampling intervals are implemented using cascaded counter which is

connected to a very accurate timing signal generated by a crystal controlled oscillator (Astable

multi-vibrator). The output timing signal of each cascade section is available at a switch which

is used to select the appropriate timing signal for controlling the sampling interval. The output

of the switch is connected to the clock input of a negative triggered J-K flip-flop, which divides

the input signal by 2. Thus, when the 1 Hz sampling interval is selected, the signal at the

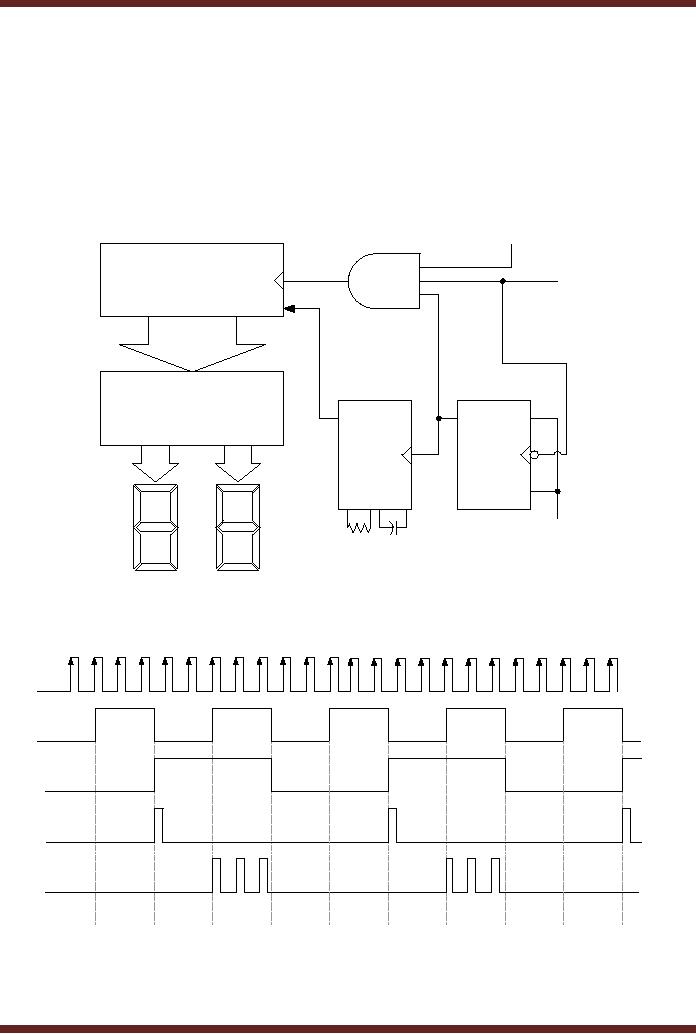
output of the J-K flip-flop has a time period of 2 seconds. Figure 30.4.

The detailed circuit diagram and the timing diagram of the frequency diagram are

shown in figure 30.5. In the timing diagram the Sampling Interval pulse is obtained from the

output of the J-K flip-flop shown in figure 30.4. The duration of the Sampling interval pulse can

be selected through the switch. The sampling interval signal is connected to the input of the 3-

input AND gate and the clock input of the second J-K flip-flop which toggles its output at each

negative transition of the clock. When the output of the second flip-flop changes to logic 1

(interval t1) it triggers the One-Shot which generates a short output pulse which clears the

316

CS302 - Digital Logic & Design

Counter circuit. At interval t2 during the positive half of the sampling interval when the output of

the second J-K flip-flop is high the 3-input AND gate is enabled and the input signal with

unknown frequency is applied at the input of the counter, which count the input signal pulses.

At interval t3 there is negative transition of the sampling signal, which triggers the second flip-

flop changing its output to logic 0. Logic 0 output of the flip-flop disables the 3-input AND gate

inhibiting the counter from counting. The pulses counted by the counter during interval t2 to t3

are directly displayed.

Input Signal with

unknown frequency

Counter

Sampling

Clear

Interval

BCD & Segment

Decoder

One

Flip-flop

Shot

Figure 30.5a Detailed circuit diagram of a frequency counter

Input

signal

Sampling

Interval

Output of

flip-flop 2

Counter

reset signal

Counter

Input

Figure 30.5b Timing diagram of the frequency counter circuit

317

CS302 - Digital Logic & Design

Design of Synchronous Counters

The counters that have been discussed are binary counters that count in a sequence

either upwards or downwards. The count start and end sequence of a counter can also be set

arbitrarily and the counter can then count up or down with in the terminal count limits.

Counters can also be designed that do not count in a sequence, instead they sequence

through a set of predefined arbitrary values. Counters can also be implemented using D flip-

flops instead of J-K flip-flops. No formal method of designing Counters has been discussed;

however during the study of synchronous counters a general procedure was discussed which

helps in the implementation of the counters. The procedure requires listing of the binary

counting sequence and then determining the input condition for each flip-flop which promotes

a change in their output state. The input conditions are dependent on the previous start

outputs of the flip-flops and are implemented by using logic gates. The method does help in

implementing counters but it is not a comprehensive method for the design and

implementation of different types of counters.

Clocked Synchronous State Machines

The Synchronous Counters are the simplest forms of Clocked Synchronous State

Machines. State Machine is a generic name given to Sequential circuits. The Sequential

circuits use a clock signal to change from one state to the other and all the flip-flops are

connected to a single clock signal, therefore it is a Clocked Synchronous State Machine.

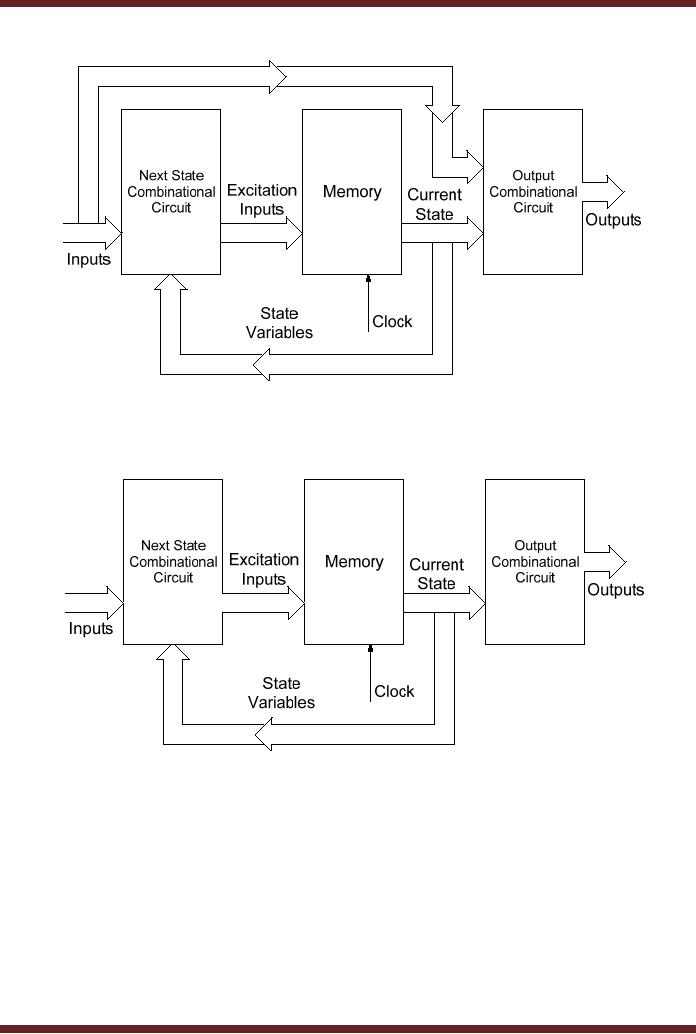
A general Sequential circuit consists of a combinational circuit and a memory element. The

memory element is made of a set of n flip-flops all connected to a a common clock. The n flip-

flops store 2n states. The flip-flops change their current state to the next state on each clock

transition. The next state is determined by the current state and the external input. The output

of the State Machine is determined by the current state and external input. The inputs to the

memory which allow the memory to change its state on a clock transition are known as

excitation inputs or excitation variables. The present state of the memory is represented by

state variables. The state variables and the inputs to the sequential circuit determine the

sequential circuit output. The Sequential circuit whose output depends on the current state and

the input is known as Mealy Machine. Figure 30.6a.

Sequential circuits whose output is

determined by the current state only is known as Moore Machine. Figure 30.6b.

318

CS302 - Digital Logic & Design

Figure 30.6a Clocked Sequential State Machine (Mealy Machine)

Figure 30.6b Clocked Sequential State Machine (Moore Machine)

Design Procedure

The design and implementation of Synchronous Counters follows an

established set of steps and rules which start from defining the state diagram and end at the

implementation of State machine.

7. State Diagram

319

CS302 - Digital Logic & Design

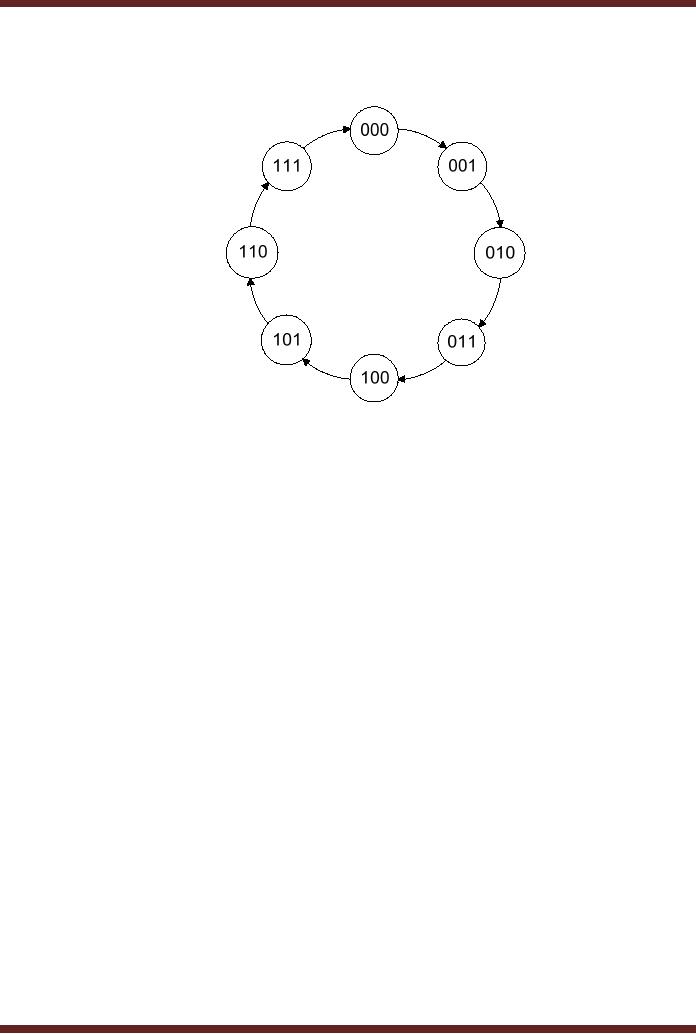
A sequential circuit (state machine) is described by a state diagram, which shows the

sequence of state through which the sequential circuit progresses when it is clocked. The state

diagram of a 3-bit Synchronous Up-Counter (sequential circuit) is shown in the figure. 30.7

Figure 30.7

State diagram of a 3-bit Up-Counter

320

Table of Contents: