 |
Definitions of Probability:MUTUALLY EXCLUSIVE EVENTS, Venn Diagram |
| << COUNTING RULES:RULE OF PERMUTATION, RULE OF COMBINATION |
| THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:ADDITION LAW >> |

MTH001
Elementary Mathematics
LECTURE #
30
Definitions of
Probability:
∑
Subjective
Approach to Probability
∑
Objective
Approach:
∑
Classical
Definition of Probability
Relative
Frequency Definition of
Probability
Before
we begin the various
definitions of probability, let us
revise the concepts
of:
∑
Mutually
Exclusive Events
∑
Exhaustive
Events
∑
Equally
Likely Events
MUTUALLY
EXCLUSIVE EVENTS:
Two
events A and B of a single
experiment are said to be
mutually exclusive or disjoint
if
and
only if they cannot both
occur at the same time
i.e. they have no points in
common.
EXAMPLE-1:
When
we toss a coin, we get
either
a head
or
a tail,
but not
both at
the same time.
The
two events head and
tail are therefore mutually
exclusive.
EXAMPLE-2:
When
a die is rolled, the events
`even number' and `odd
number' are mutually
exclusive as
we
can get either an even
number or an odd number in
one throw, not both at
the same
time.
Similarly, a student either
qualifies
or
fails, a
person is either a teenager or
not a
teenager,
etc., etc.
Three
or more events originating
from the same experiment
are mutually exclusive
if
pair
wise they are mutually
exclusive.
If
the two events can
occur at
the same time, they
are not mutually exclusive,
e.g., if we
draw
a card from an ordinary deck
of 52 playing cars, it can
be both a
king and a diamond.
Therefore,
kings and diamonds are
not mutually exclusive.
Speaking of playing
cards,
it is to be remembered that an ordinary
deck of playing cards
contains 52 cards
arranged
in 4 suits of 13 each. The
four suits are called
diamonds, hearts, clubs
and
spades;
the first two are
red and the last
two are black. The
face values called
denominations,
of the 13 cards in each suit
are ace, 2, 3, ..., 10,
jack, queen and king.
The
face
values called denominations, of
the 13 cards in each suit
are ace, 2, 3, ..., 10,
jack,
queen
and king.
We
have discussed the concepts
of mutually exclusive
events.
Another
important concept is that of
exhaustive events.
EXHAUSTIVE
EVENTS:
Events
are said to be collectively
exhaustive, when the union
of mutually
exclusive
events is equal to the
entire sample space
S.
EXAMPLES:
1.
In the
coin-tossing experiment, `head'
and `tail' are collectively
exhaustive events.
2.
In the
die-tossing experiment, `even
number' and `odd number'
are collectively
exhaustive
events.
In
conformity with what was
discussed in the last
lecture:
PARTITION
OF THE SAMPLE
SPACE:
A
group of mutually exclusive
and exhaustive events
belonging to a sample space
is
called
a partition of the sample
space. With reference to any
sample space S, events A
and
⎯A form a
partition as they are
mutually exclusive and their
union is the entire sample
space.
The
Venn D
iagram
below clearly indicates this
point.
Page
212
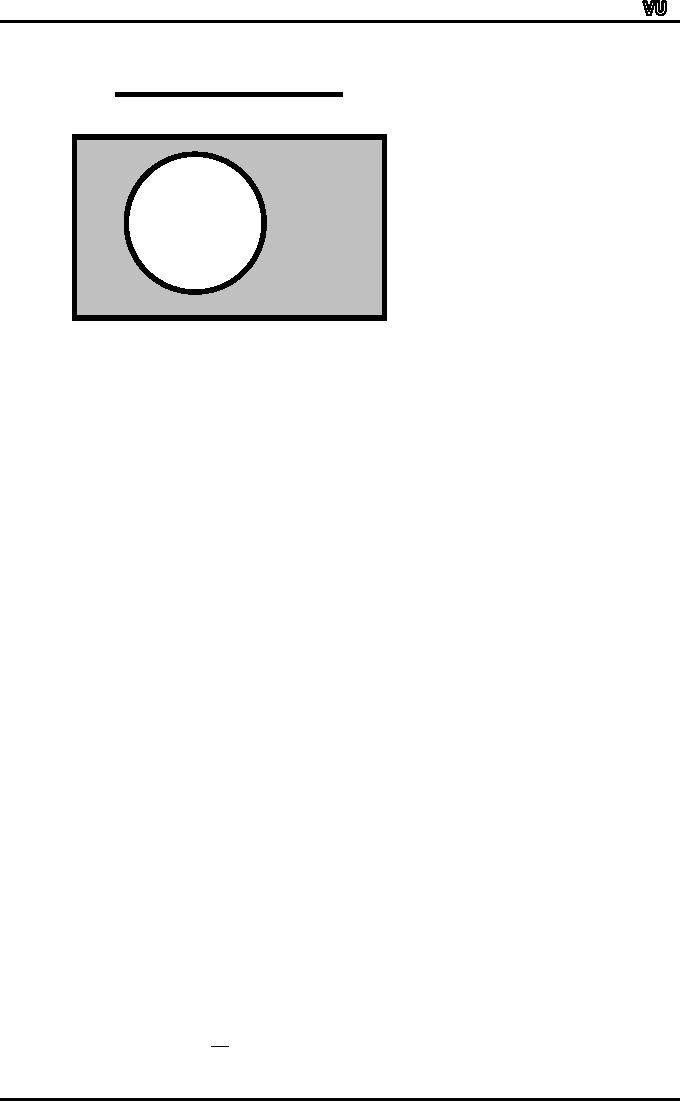
MTH001
Elementary Mathematics
Venn
Diagram
A
S
⎯A is
shaded
Next,
we consider the concept of
equally likely
events:
EQUALLY
LIKELY EVENTS:
Two
events A and B are said to
be equally likely, when one
event is as likely to
occur
as
the other.
In
other words, each event
should occur in equal number
in repeated trials.
EXAMPLE:
When
a fair coin is tossed, the
head is as likely to appear as
the tail, and
the
proportion
of times each side is
expected to appear is
1/2.
EXAMPLE:
If
a card is drawn out of a
deck of well-shuffled cards,
each card is equally likely
to
be
drawn, and the proportion of
times each card can be
expected to be drawn in a very
large
number of draws is 1/52.Having
discussed basic concepts
related to probability
theory,
we
now begin the discussion of
THE CONCEPT AND DEFINITIONS OF
PROBABILITY.
Probability
can be discussed from two
points of view: the
subjective approach, and
the
objective
approach.
SUBJECTIVE
OR PERSONALISTIC PROBABILITY:
As
its name suggests, the
subjective or personalistic probability
is a measure of the
strength
of a person's belief regarding
the occurrence of an event A.
Probability in this
sense
is purely subjective, and is
based on whatever evidence is
available to the
individual.
It
has a disadvantage that two
or more persons faced with
the same evidence may
arrive at
different
probabilities.
For
example, suppose that a
panel of three judges is
hearing a trial. It is
possible
that,
based on the evidence that
is presented, two of them
arrive at the conclusion
that the
accused
is guilty while one of them
decides that the evidence is
NOT strong enough to
draw
this
conclusion.
On
the other hand, objective
probability relates to
those situations where
everyone will
arrive
at the same
conclusion.
It
can be classified into two
broad categories, each of
which is briefly described as
follows:
1.
The Classical or `A Priori'
Definition of Probability
If
a random experiment can
produce n mutually exclusive
and equally likely
outcomes,
and if m out to these
outcomes are considered
favorable to the occurrence of
a
certain
event A, then the
probability of the event A,
denoted by P(A), is defined as
the ratio
m/n.
Symbolically,
we write
m
P(A
)
=
n
Number
of favourable outcomes
=
Total
number of possible outcomes
Page
213

MTH001
Elementary Mathematics
This
definition was formulated by the
French mathematician P.S.
Laplace (1949-1827)
and
can
be very conveniently used in
experiments where the total
number of possible
outcomes
and
the number of outcomes
favourable to an event can be
DETERMINED.
Let
us now consider a few
examples to illustrate the
classical definition of
probability:
EXAMPLE-1:
If
a card is drawn from an
ordinary deck of 52 playing
cards, find the probability
that
i)
the card is a red card,
ii) the card is a
10.
SOLUTION
:
The
total number of possible
outcomes is 13+13+13+13 = 52,
and we assume that
all
possible
outcomes are equally
likely.(It is well-known that an
ordinary deck of cards
contains
13
cards of diamonds, 13 cards of
hearts, 13 cards of clubs,
and 13 cards of
spades.)
(i)
Let A represent the event
that the card drawn is a
red card.
Then
the number of outcomes
favourable to the event A is 26
(since the 13 cards
of
diamonds
and the 13 cards of hearts
are red).
He
nce
m
P(A
)
=
n
Number
of favourable outcomes
=
Total
number of possible
outcomes
26
1
=
=
52
2
4
1
P(B)
=
= .
Thus
EXAMPLE-2:
A
fair coin is tossed three
times. Wha52
th13
robability
that at least one head
appears?
t
is e p
SOLUTION:
The
sample space for this
experiment is
S=
{HHH,
HHT, HTH, THH,
HTT,
THT, TTH, TTT}
and
thus the total number of
sample points is 8
i.e.
n(S) = 8.Let A denote the
event that at least one
head appears. Then
A=
{HHH,
HHT, HTH,
THH,
HTT, THT, TTH}
and
therefore n(A) = 7.
He
nce
n(A
)
7
P(A
)
=
= .
n(S)
8
EXAMPLE-3:
Four
items are taken at random
from a box of 12 items and
inspected. The box is
rejected
if
more
than 1 item is found to be
faulty. If there are 3
faulty items in the box,
find the
probability
that the box is accepted.
SOLUTION:
⎛12 ⎞
⎜
⎟ = 495
⎜
4⎟
⎝ ⎠
Page
214

MTH001
Elementary Mathematics
The
sample space S
contains
sample
points
⎛12 ⎞
⎜ ⎟
(because
there are ⎜
4
⎟
⎝ ⎠
ways
of selecting four items out
of twelve).
The
box contains 3 faulty and 9
good items. The box is
accepted if there is (i) no
faulty
items,
or (ii) one faulty item in
the sample of 4 items
selected.
Let
A denote the event the
number of faulty items
chosen is 0 or 1.
Then
⎛
3
⎞ ⎛
9
⎞ ⎛
3⎞
⎛ 9
⎞
n( A)
=
⎜ ⎟ ⎜ ⎟ + ⎜ ⎟⎜ ⎟
⎜
0
⎟ ⎜
4
⎟
⎜1
⎟ ⎜
3
⎟
⎝
⎠ ⎝ ⎠ ⎝ ⎠⎝ ⎠
=
126
+
252
=
378
sample
po int
s.
m
378
P(A
)
=
∴
=
=
0.76
n
495
Hence
the
probability
that
the
box
is
accepted
is
76%
(in
spite of the fact that
the box contains
3 faulty
items).
The
classical definition has the
following shortcomings:
i)
This definition is said to
involve circular reasoning as
the term equally likely
really means
equally
probable.
Thus
probability is defined by introducing
concepts that presume a
prior
knowledge of
the
meaning
of
probability.
ii)
This definition becomes
vague when the possible
outcomes are INFINITE in
number, or
uncountable.
iii)
This definition is NOT
applicable when the
assumption of equally likely
does not
hold.
And
the fact of the matter is
that there are NUMEROUS
situations where the
assumption of
equally
likely cannot hold.
And
these are the situations
where we have to look for
another definition of
probability!
The
other
definition of
probability under the
objective approach is the
relative
frequency
definition of probability.
The
essence of this definition is
that if an experiment is repeated a
large number of
times
under (more or less)
identical conditions, and if
the event of our interest
occurs a
certain
number of times, then the
proportion
in which
this event occurs is
regarded as the
probability
of that event.
For
example, we know that a
large number of students sit
for the matric
examination
every
year. Also, we know that a
certain proportion of these
students will obtain the
first
division,
a certain proportion will
obtain the second division,
--- and a certain proportion
of
the
students will fail.
Since
the total number of students
appearing for the matric
exam is very large,
hence:
∑
The
proportion of students who
obtain the first division
--- this proportion can
be
regarded
as the probability
of obtaining
the first division,
∑
The
proportion of students who
obtain the second division
--- this proportion can
be
regarded
as the probability
of obtaining
the second division, and so
on.
Page
215
Table of Contents:
- Recommended Books:Set of Integers, SYMBOLIC REPRESENTATION
- Truth Tables for:DE MORGANíS LAWS, TAUTOLOGY
- APPLYING LAWS OF LOGIC:TRANSLATING ENGLISH SENTENCES TO SYMBOLS
- BICONDITIONAL:LOGICAL EQUIVALENCE INVOLVING BICONDITIONAL
- BICONDITIONAL:ARGUMENT, VALID AND INVALID ARGUMENT
- BICONDITIONAL:TABULAR FORM, SUBSET, EQUAL SETS
- BICONDITIONAL:UNION, VENN DIAGRAM FOR UNION
- ORDERED PAIR:BINARY RELATION, BINARY RELATION
- REFLEXIVE RELATION:SYMMETRIC RELATION, TRANSITIVE RELATION
- REFLEXIVE RELATION:IRREFLEXIVE RELATION, ANTISYMMETRIC RELATION
- RELATIONS AND FUNCTIONS:FUNCTIONS AND NONFUNCTIONS
- INJECTIVE FUNCTION or ONE-TO-ONE FUNCTION:FUNCTION NOT ONTO
- SEQUENCE:ARITHMETIC SEQUENCE, GEOMETRIC SEQUENCE:
- SERIES:SUMMATION NOTATION, COMPUTING SUMMATIONS:
- Applications of Basic Mathematics Part 1:BASIC ARITHMETIC OPERATIONS
- Applications of Basic Mathematics Part 4:PERCENTAGE CHANGE
- Applications of Basic Mathematics Part 5:DECREASE IN RATE
- Applications of Basic Mathematics:NOTATIONS, ACCUMULATED VALUE
- Matrix and its dimension Types of matrix:TYPICAL APPLICATIONS
- MATRICES:Matrix Representation, ADDITION AND SUBTRACTION OF MATRICES
- RATIO AND PROPORTION MERCHANDISING:Punch recipe, PROPORTION
- WHAT IS STATISTICS?:CHARACTERISTICS OF THE SCIENCE OF STATISTICS
- WHAT IS STATISTICS?:COMPONENT BAR CHAR, MULTIPLE BAR CHART
- WHAT IS STATISTICS?:DESIRABLE PROPERTIES OF THE MODE, THE ARITHMETIC MEAN
- Median in Case of a Frequency Distribution of a Continuous Variable
- GEOMETRIC MEAN:HARMONIC MEAN, MID-QUARTILE RANGE
- GEOMETRIC MEAN:Number of Pupils, QUARTILE DEVIATION:
- GEOMETRIC MEAN:MEAN DEVIATION FOR GROUPED DATA
- COUNTING RULES:RULE OF PERMUTATION, RULE OF COMBINATION
- Definitions of Probability:MUTUALLY EXCLUSIVE EVENTS, Venn Diagram
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:ADDITION LAW
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:INDEPENDENT EVENTS