Branching: Comparison and Conditions, Conditional ,Unconditional Jump

<< Addressing Modes: Data Declaration, Direct, Register Indirect , Offset Addressing

Manipulations: Multiplication Algorithm, Shifting and Rotations, Bitwise Logical Operations >>

Branching

3.1. COMPARISON AND CONDITIONS

Conditional jump was introduced in the last chapter to loop for the

addition of a fixed number of array elements. The jump was based on the

zero flag. There are many other conditions possible in a program. For

example an operand can be greater than another operand or it can be

smaller. We use comparisons and boolean expressions extensively in higher

level languages. They must be available is some form in assembly language,

otherwise they could not possibly be made available in a higher level

language. In fact they are available in a very fine and purified form.

The basic root instruction for all comparisons is CMP standing for

compare. The operation of CMP is to subtract the source operand from the

destination operand, updating the flags without changing either the source

or the destination. CMP is one of the key instructions as it introduces the

capability of conditional routing in the processor.

A closer thought reveals that with subtraction we can check many different

conditions. For example if a larger number is subtracted from a smaller

number then borrow is needed. The carry flag plays the role of borrow during

the subtraction operation. And in this condition the carry flag will be set. If

two equal numbers are subtracted the answer is zero and the zero flag will be

set. Every significant relation between the destination and source is evident

from the sign flag, carry flag, zero flag, and the overflow flag. CMP is

meaningless without a conditional jump immediately following it.

Another important distinction at this point is the difference between signed

and unsigned numbers. In unsigned numbers only the magnitude of the

number is important, whereas in signed numbers both the magnitude and

the sign are important. For example -2 is greater than -3 but 2 is smaller

than 3. The sign has affected our comparisons.

Inside the computer signed numbers are represented in two's complement

notation. In essence a number in this representation is still a number, just

that now our interpretation of this number will be signed. Whether we use

jump above and below or we use jump greater or less will convey our

intention to the processor. The jump above and greater operations at first

sight seem to be doing the same operation, and similarly below and less

operations seem to be similar. However for signed numbers JG and JL will

work properly and for unsigned JA and JB will work properly and not the

other way around.

It is important to note that at the time of comparison, the intent of the

programmer to treat the numbers as signed or unsigned is not clear. The

subtraction in CMP is a normal subtraction. It is only after the comparison,

during the conditional jump operation, that the intent is conveyed. At that

time with a specific combination of flags checked the intent is satisfied.

For example a number 2 is represented in a word as 0002 while the

number -2 is represented as FFFE. In a byte they would be represented as 02

and FE. Now both have the same magnitude however the different sign has

caused very different representation in two's complement form. Now if the

intent is to use FFFE or decimal 65534 then the same data would be placed

in the word as in case of -2. In fact if -2 and 65534 are compared the

processor will set the zero flag signaling that they are exactly equal. As

regards an unsigned comparison the number 65534 is much greater than 2.

Computer Architecture & Assembly Language Programming

Course Code: CS401

CS401@vu.edu.pk

So if a JA is taken after comparing -2 in the destination with 2 in the source

the jump will be taken. If however JG is used after the same comparison the

jump will not be taken as it will consider the sign and with the sign -2 is

smaller than 2. The key idea is that -2 and 65534 were both stored in

memory in the same form. It was the interpretation that treated it as a signed

or as an unsigned number.

The unsigned comparisons see the numbers as 0 being the smallest and

65535 being the largest with the order that 0 < 1 < 2 ... < 65535. The signed

comparisons see the number -32768 which has the same memory

representation as 32768 as the smallest number and 32767 as the largest

with the order -32768 < -32767 < ... < -1 < 0 < 1 < 2 < ... < 32767. All the

negative numbers have the same representation as an unsigned number in

the range 32768 ... 65535 however the signed interpretation of the signed

comparisons makes them be treated as negative numbers smaller than zero.

All meaningful situations both for signed and unsigned numbers than

occur after a comparison are detailed in the following table.

DEST = SRC

ZF = 1

When the source is subtracted

from the destination and both are

equal the result is zero and

therefore the zero flag is set. This

works for both signed and

unsigned numbers.

UDEST < USRC

CF = 1

When an unsigned source is

subtracted from an unsigned

destination and the destination is

smaller, borrow is needed which

sets the carry flag.

ZF = 1 OR CF = 1

If the zero flag is set, it means

UDEST ≤ USRC

that the source and destination

are equal and if the carry flag is

set it means a borrow was needed

in the subtraction and therefore

the destination is smaller.

CF = 0

When an unsigned source is

UDEST ≥ USRC

subtracted from an unsigned

destination no borrow will be

needed either when the operands

are equal or when the destination

is greater than the source.

UDEST > USRC

ZF = 0 AND CF = 0

The

unsigned

source

and

destination are not equal if the

zero flag is not set and the

destination is not smaller since

no borrow was taken. Therefore

the destination is greater than

the source.

SDEST < SSRC

When a signed source is

SF ≠ OF

subtracted

from

signed

destination and the answer is

negative with no overflow than

the destination is smaller than

the source. If however there is an

overflow meaning that the sign

has changed unexpectedly, the

meanings are reversed and a

Computer Architecture & Assembly Language Programming

Course Code: CS401

CS401@vu.edu.pk

positive number signals that the

destination is smaller.

If the zero flag is set, it means

SDEST ≤ SSRC

ZF = 1 OR SF ≠ OF

that the source and destination

are equal and if the sign and

overflow flags differ it means that

the destination is smaller as

described above.

SF = OF

When a signed source is

SDEST ≥ SSRC

subtracted

from

signed

destination and the answer is

positive with no overflow than the

destination is greater than the

source. When an overflow is there

signaling that sign has changed

unexpectedly, we interpret a

negative answer as the signal

that the destination is greater.

SDEST > SSRC

ZF = 0 AND SF = OF

If the zero flag is not set, it means

that the signed operands are not

equal and if the sign and overflow

match in addition to this it

means that the destination is

greater than the source.

3.2. CONDITIONAL JUMPS

For every interesting or meaningful situation of flags, a conditional jump is

there. For example JZ and JNZ check the zero flag. If in a comparison both

operands are same, the result of subtraction will be zero and the zero flag

will be set. Thus JZ and JNZ can be used to test equality. That is why there

are renamed versions JE and JNE read as jump if equal or jump if not equal.

They seem more logical in writing but mean exactly the same thing with the

same opcode. Many jumps are renamed with two or three names for the

same jump, so that the appropriate logic can be conveyed in assembly

language programs. This renaming is done by Intel and is a standard for

iAPX88. JC and JNC test the carry flag. For example we may need to test

whether there was an overflow in the last unsigned addition or subtraction.

Carry flag will also be set if two unsigned numbers are subtracted and the

first is smaller than the second. Therefore the renamed versions JB, JNAE,

and JNB, JAE are there standing for jump if below, jump if not above or

equal, jump if not below, and jump if above or equal respectively. The

operation of all jumps can be seen from the following table.

Jump if carry

CF = 1

This jump is taken if

Jump if below

the last arithmetic

JNAE

Jump if not above or equal

operation generated a

carry or required a

borrow. After a CMP it

taken

the

unsigned source is

smaller

than

the

unsigned destination.

JNC

Jump if not carry

CF = 0

This jump is taken if

JNB

Jump if not below

the last arithmetic

JAE

Jump if above or equal

operation

did

not

Computer Architecture & Assembly Language Programming

Course Code: CS401

CS401@vu.edu.pk

generated a carry or

required a borrow.

After a CMP it is taken

if the unsigned source

is larger or equal to

the

unsigned

destination.

Jump if equal

ZF = 1

This jump is taken if

Jump if zero

the last arithmetic

operation produced a

zero in its destination.

After a CMP it is taken

if both operands were

equal.

JNE

Jump if not equal

ZF = 0

This jump is taken if

JNZ

Jump if not zero

the last arithmetic

operation

did

not

produce a zero in its

destination. After a

CMP it is taken if both

operands

were

different.

Jump if above

ZF = 0 AND

This jump is taken

JNBE

Jump if not below or equal

CF = 0

after a CMP if the

unsigned source is

larger

than

the

unsigned destination.

JNA

Jump if not above

ZF = 1 OR

This jump is taken

JBE

Jump if not below or equal

CF = 1

after a CMP if the

unsigned source is

smaller than or equal

the

unsigned

destination.

This jump is taken

Jump if less

SF ≠ OF

after a CMP if the

JNGE

Jump if not greater or equal

signed

source

smaller

than

the

signed destination.

JNL

Jump if not less

SF = OF

This jump is taken

JGE

Jump if greater or equal

after a CMP if the

signed source is larger

than or equal to the

signed destination.

Jump if greater

ZF = 0 AND

This jump is taken

JNLE

Jump if not less or equal

SF = OF

after a CMP if the

signed source is larger

than

the

signed

destination.

JNG

Jump if not greater

ZF = 1 OR

This jump is taken

JLE

Jump if less or equal

after a CMP if the

SF ≠ OF

signed

source

smaller than or equal

the

signed

destination.

Computer Architecture & Assembly Language Programming

Course Code: CS401

CS401@vu.edu.pk

Jump if overflow.

OF = 1

This jump is taken if

the last arithmetic

operation changed the

sign unexpectedly.

JNO

Jump if not overflow

OF = 0

This jump is taken if

the last arithmetic

operation

did

not

change

the

sign

unexpectedly.

Jump if sign

SF = 1

This jump is taken if

the last arithmetic

operation produced a

negative number in its

destination.

JNS

Jump if not sign

SF = 0

This jump is taken if

the last arithmetic

operation produced a

positive number in its

destination.

Jump if parity

PF = 1

This jump is taken if

JPE

Jump if even parity

the last arithmetic

operation produced a

number

its

destination that has

even parity.

JNP

Jump if not parity

PF = 0

This jump is taken if

JPO

Jump if odd parity

the last arithmetic

operation produced a

number

its

destination that has

odd parity.

JCXZ

Jump if CX is zero

CX = 0

This jump is taken if

the CX register is zero.

The CMP instruction sets the flags reflecting the relation of the destination

to the source. This is important as when we say jump if above, then what is

above what. The destination is above the source or the source is above the

destination.

The JA and JB instructions are related to unsigned numbers. That is our

interpretation for the destination and source operands is unsigned. The 16th

bit holds data and not the sign. In the JL and JG instructions standing for

jump if lower and jump if greater respectively, the interpretation is signed.

The 16th bit holds the sign and not the data. The difference between them

will be made clear as an elaborate example will be given to explain the

difference.

One jump is special that it is not dependant on any flag. It is JCXZ, jump

if the CS register is zero. This is because of the special treatment of the CX

counterpart or not form of this instruction.

The adding numbers example of the last chapter can be a little simplified

using the compare instruction on the BX register and eliminating the need

for a separate counter as below.

Computer Architecture & Assembly Language Programming

Course Code: CS401

CS401@vu.edu.pk

Example 3.1

001

; a program to add ten numbers without a separate counter

002

[org 0x0100]

003

mov bx, 0

; initialize array index to zero

004

mov ax, 0

; initialize sum to zero

005

006

l1:

add

ax, [num1+bx]

;

add number to ax

007

add

bx, 2

;

advance bx to next index

008

cmp

bx, 20

;

are we beyond the last index

009

jne

;

if not add next number

010

011

mov

[total], ax

; write back sum in memory

012

013

mov

ax, 0x4c00

; terminate program

014

int

0x21

015

016

num1:

10, 20, 30, 40, 50, 10, 20, 30, 40, 50

017

total:

The format of memory access is still base + offset.

006

BX is used as the array index as well as the counter. The offset of

008

11th number will be 20, so as soon as BX becomes 20 just after the

10th number has been added, the addition is stopped.

The jump is displayed as JNZ in the debugger even though we have

009

written JNE in our example. This is because it is a renamed jump

with the same opcode as JNZ and the debugger has no way of

knowing the mnemonic that we used after looking just at the

opcode. Also every code and data reference that we used till now is

seen in the opcode as well. However for the jump instruction we see

an operand of F2 in the opcode and not 0116. This will be discussed

in detail with unconditional jumps. It is actually a short relative

jump and the operand is stored in the form of positive or negative

offset from this instruction.

With conditional branching in hand, there are just a few small things left

in assembly language that fills some gaps. Now there is just imagination and

the skill to conceive programs that can make you write any program.

3.3. UNCONDITIONAL JUMP

Till now we have been placing data at the end of code. There is no such

restriction and we can define data anywhere in the code. Taking the previous

example, if we place data at the start of code instead of at the end and we

load our program in the debugger. We can see our data placed at the start

but the debugger is intending to start execution at our data. The COM file

definition said that the first executable instruction is at offset 0100 but we

have placed data there instead of code. So the debugger will try to interpret

that data as code and showed whatever it could make up out of those

opcodes.

We introduce a new instruction called JMP. It is the unconditional jump

that executes regardless of the state of all flags. So we write an unconditional

jump as the very first instruction of our program and jump to the next

instruction that follows our data declarations. This time 0100 contains a

valid first instruction of our program.

Example 3.2

001

; a program to add ten numbers without a separate counter

002

[org 0x0100]

003

jmp start

; unconditionally jump over data

004

005

num1:

10, 20, 30, 40, 50, 10, 20, 30, 40, 50

006

total:

Computer Architecture & Assembly Language Programming

Course Code: CS401

CS401@vu.edu.pk

007

008

start:

mov

bx, 0

; initialize array index to zero

009

mov

ax, 0

; initialize sum to zero

010

011

l1:

add

ax, [num1+bx]

;

add number to ax

012

add

bx, 2

;

advance bx to next index

013

cmp

bx, 20

;

are we beyond the last index

014

jne

;

if not add next number

015

016

mov

[total], ax

; write back sum in memory

017

018

mov

ax, 0x4c00

; terminate program

019

int

0x21

JMP jumps over the data declarations to the start label and

003

execution resumes from there.

3.4. RELATIVE ADDRESSING

Inside the debugger the instruction is shown as JMP 0119 and the location

0119 contains the original first instruction of the logic of our program. This

jump is unconditional, it will always be taken. Now looking at the opcode we

see F21600 where F2 is the opcode and 1600 is the operand to it. 1600 is

0016 in proper word order. 0119 is not given as a parameter rather 0016 is

given.

This is position relative addressing in contrast to absolute addressing. It is

not telling the exact address rather it is telling how much forward or

backward to go from the current position of IP in the current code segment.

So the instruction means to add 0016 to the IP register. At the time of

execution of the first instruction at 0100 IP was pointing to the next

instruction at 0103, so after adding 16 it became 0119, the desired target

location. The mechanism is important to know, however all calculations in

this mechanism are done by the assembler and by the processor. We just use

a label with the JMP instruction and are ensured that the instruction at the

target label will be the one to be executed.

3.5. TYPES OF JUMP

The three types of jump, near, short, and far, differ in the size of

instruction and the range of memory they can jump to with the smallest

short form of two bytes and a range of just 256 bytes to the far form of five

bytes and a range covering the whole memory.

Short Jump

Disp

Near Jump

Disp Low

Disp High

Far Jump

IP Low

IP High

CS Low

CS High

Near Jump

When the relative address stored with the instruction is in 16 bits as in the

last example the jump is called a near jump. Using a near jump we can jump

anywhere within a segment. If we add a large number it will wrap around to

Computer Architecture & Assembly Language Programming

Course Code: CS401

CS401@vu.edu.pk

the lower part. A negative number actually is a large number and works this

way using the wraparound behavior.

Short Jump

If the offset is stored in a single byte as in 75F2 with the opcode 75 and

operand F2, the jump is called a short jump. F2 is added to IP as a signed

byte. If the byte is negative the complement is negated from IP otherwise the

byte is added. Unconditional jumps can be short, near, and far. The far type

is yet to be discussed. Conditional jumps can only be short. A short jump

can go +127 bytes ahead in code and -128 bytes backwards and no more.

This is the limitation of a byte in singed representation.

Far Jump

Far jump is not position relative but is absolute. Both segment and offset

must be given to a far jump. The previous two jumps were used to jump

within a segment. Sometimes we may need to go from one code segment to

another, and near and short jumps cannot take us there. Far jump must be

used and a two byte segment and a two byte offset are given to it. It loads CS

wit the segment part and IP with the offset part. Execution therefore resumes

from that location in physical memory. The three instructions that have a far

form are JMP, CALL, and RET, are related to program control. Far capability

makes intra segment control possible.

3.6. SORTING EXAMPLE

Moving ahead from our example of adding numbers we progress to a

program that can sort a list of numbers using the tools that we have

accumulated till now. Sorting can be ascending or descending like if the

largest number comes at the top, followed by a smaller number and so on till

the smallest number the sort will be called descending. The other order

starting with the smallest number and ending at the largest is called

ascending sort. This is a common problem and many algorithms have been

developed to solve it. One simple algorithm is the bubble sort algorithm.

In this algorithm we compare consecutive numbers. If they are in required

order e.g. if it is a descending sort and the first is larger then the second,

then we leave them as it is and if they are not in order, we swap them. Then

we do the same process for the next two numbers and so on till the last two

are compared and possibly swapped.

A complete iteration is called a pass over the array. We need N passes at

least in the simplest algorithm if N is the number of elements to be sorted. A

finer algorithm is to check if any swap was done in this pass and stop as

soon as a pass goes without a swap. The array is now sorted as every pair of

elements is in order.

For example if our list of numbers is 60, 55, 45, and 58 and we want to

sort them in ascending order, the first comparison will be of 60 and 55 and

as the order will be reversed to 55 and 60. The next comparison will be of 60

and 45 and again the two will be swapped. The next comparison of 60 and 58

will also cause a swap. At the end of first pass the numbers will be in order

of 55, 45, 58, and 60. Observe that the largest number has bubbled down to

the bottom. Just like a bubble at bottom of water. In the next pass 55 and 45

will be swapped. 55 and 58 will not be swapped and 58 and 60 will also not

be swapped. In the next pass there will be no swap as the elements are in

order i.e. 45, 55, 58, and 60. The passes will be stopped as the last pass did

not cause any swap. The application of bubble sort on these numbers is

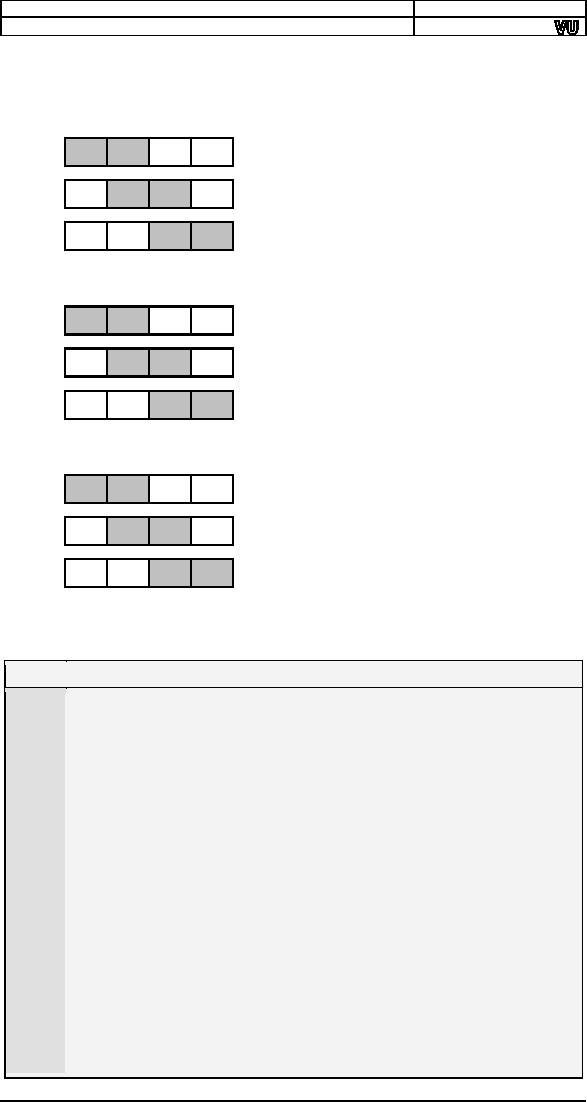
further explained with the following illustration.

Computer Architecture & Assembly Language Programming

Course Code: CS401

CS401@vu.edu.pk

State of Data

Swap Done

Swap Flag

Pass 1

Off

Yes

Pass 2

Off

Yes

Pass 3

Off

No more passes since swap flag is Off

Example 3.3

001

; sorting a list of ten numbers using bubble sort

002

[org 0x0100]

003

jmp start

004

005

data:

60, 55, 45, 50, 40, 35, 25, 30, 10, 0

006

swap:

007

008

start:

mov

bx, 0

; initialize array index to zero

009

mov

byte [swap], 0

; rest swap flag to no swaps

010

011

loop1:

mov

ax, [data+bx]

; load number in ax

012

cmp

ax, [data+bx+2]

; compare with next number

013

jbe

noswap

; no swap if already in order

014

015

mov

dx, [data+bx+2]

;

load second element in dx

016

mov

[data+bx+2], ax

;

store first number in second

017

mov

[data+bx], dx

;

store second number in first

018

mov

byte [swap], 1

;

flag that a swap has been done

019

020

noswap:

add

bx, 2

; advance bx to next index

021

cmp

bx, 18

; are we at last index

022

jne

loop1

; if not compare next two

023

024

cmp

byte [swap], 1

; check if a swap has been done

025

bsort

; if yes make another pass

026

027

mov

ax, 0x4c00

; terminate program

028

int

0x21

Computer Architecture & Assembly Language Programming

Course Code: CS401

CS401@vu.edu.pk

The jump instruction is placed to skip over data.

003

The swap flag can be stored in a register but as an example it is

006

stored in memory and also to extend the concept at a later stage.

One element is read in AX and it is compared with the next element

011-012

because memory to memory comparisons are not allowed.

If the JBE is changed to JB, not only the unnecessary swap on equal

013

will be performed, there will be a major algorithmic flaw due to a

logical error as in the case of equal elements the algorithm will never

stop. JBE won't swap in the case of equal elements.

The swap is done using DX and AX registers in such a way that the

015-017

values are crossed. The code uses the information that one of the

elements is already in the AX register.

This time BX is compared with 18 instead of 20 even though the

021

number of elements is same. This is because we pick an element

and compare it with the next element. When we pick the 9th element

we compare it with the next element and this is the last comparison,

since if we pick the 10th element we will compare it with the 11th

element and there is no 11th element in our case.

If a swap is done we repeat the whole process for possible more

024-025

swaps.

Inside the debugger we observe that the JBE is changed to JNA due to the

same reason as discussed for JNE and JNZ. The passes change the data in

the same manner as we presented in our illustration above. If JBE in the

code is changed to JAE the sort will change from ascending to descending.

For signed numbers we can use JLE and JGE respectively for ascending and

descending sort.

To clarify the difference of signed and unsigned jumps we change the data

array in the last program to include some negative numbers as well. When

JBE will be used on this data, i.e. with unsigned interpretation of the data

and an ascending sort, the negative numbers will come at the end after the

largest positive number. However JLE will bring the negative numbers at the

very start of the list to bring them in proper ascending order according to a

signed interpretation, even though they are large in magnitude. The data

used is shown as below.

data:

dw 60, 55, 45, 50, -40, -35, 25, 30, 10, 0

This data includes some signed numbers as well. The JBE instruction will

treat this data as an unsigned number and will cater only for the magnitude

ignoring the sign. If the program is loaded in the debugger, the numbers will

appear in their hexadecimal equivalent. The two numbers -40 and -35 are

especially important as they are represented as FFD8 and FFDD. This data is

not telling whether it is signed or unsigned. Our interpretation will decide

whether it is a very large unsigned number or a signed number in two's

complement form.

If the sorting algorithm is applied on the above data with JBE as the

comparison instruction to sort in ascending order with unsigned

interpretation, observe the comparisons of the two numbers FFD8 and

FFDD. For example it will decide that FFDD > FFD8 since the first is larger

in magnitude. At the end of sorting FFDD will be at the end of the list being

declared the largest number and FFD8 will precede it to be the second

largest.

If however the comparison instruction is changed to JLE and sorting is

done on the same data it works similarly except on the two numbers FFDD

and FFD8. This time JLE declares them to be smaller than every other

number and also declares FFDD < FFD8. At the end of sorting, FFDD is

Computer Architecture & Assembly Language Programming

Course Code: CS401

CS401@vu.edu.pk

declared to be the smallest number followed by FFD8 and then 0000. This is

in contrast to the last example where JBE was used. This happened because

JLE interpreted our data as signed numbers, and as a signed number FFDD

has its sign bit on signaling that it is a negative number in two's complement

form which is smaller than 0000 and every positive number. However JBE

did not give any significance to the sign bit and included it in the magnitude.

Therefore it declared the negative numbers to be the largest numbers.

If the required interpretation was of signed numbers the result produced

by JLE is correct and if the required interpretation was of unsigned numbers

the result produced by JBE is correct. This is the very difference between

signed and unsigned integers in higher level languages, where the compiler

takes the responsibility of making the appropriate jump depending on the

type of integer used. But it is only at this level that we can understand the

actual mechanism going on. In assembly language, use of proper jump is the

responsibility of the programmer, to convey the intentions to use the data as

signed or as unsigned.

The remaining possibilities of signed descending sort and unsigned

descending sort can be done on the same lines and are left as an exercise.

Other conditional jumps work in the same manner and can be studied from

the reference at the end. Several will be discussed in more detail when they

are used in subsequent chapters.

EXERCISES

1. Which registers are changed by the CMP instruction?

2. What are the different types of jumps available? Describe position

relative addressing.

3. If AX=8FFF and BX=0FFF and "cmp ax, bx" is executed, which of the

following jumps will be taken? Each part is independent of others. Also

give the value of Z, S, and C flags.

a. jg greater

b. jl smaller

c. ja above

d. jb below

4. Write a program to find the maximum number and the minimum

number from an array of ten numbers.

5. Write a program to search a particular element from an array using

binary search. If the element is found set AX to one and otherwise to

zero.

6. Write a program to calculate the factorial of a number where factorial

is defined as:

factorial(x) = x*(x-1)*(x-2)*...*1

factorial(0) = 1

Table of Contents: