 |
APPLICATION OF PRESENT VALUE CONCEPTS:Compound Annual Rates |
| << TIME VALUE OF MONEY:Future Value, Present Value |
| BOND PRICING & RISK:Valuing the Principal Payment, Risk >> |
Money
& Banking MGT411
VU
Lesson
9
APPLICATION
OF PRESENT VALUE CONCEPTS
Application
of Present Value Concept
Compound
Annual Rate
Interest
Rates vs. Discount
Rate
Internal
Rate of Return
Bond
Pricing
Important
Properties of Present
Value
Present
Value is higher:
The
higher the future value (FV)
of the payment
The
shorter the time period until
payment (n)
The
lower the interest rate (i)
The
size of the payment
(FVn)
Doubling
the future value of the payment
(without changing time of the
payment or interest
rate),
doubles the present value
At
5% interest rate, $100 payment has a PV
of $90.70
Doubling
it to $200, doubles the PV to
$181.40
Increasing
or decreasing FVn by
any percentage will change
PV by the same percentage in the
same
direction
The
time until the payment is
made (n)
Continuing
with the previous example of
$100 at 5%, we allow the
time to go from 0 to 30
years.
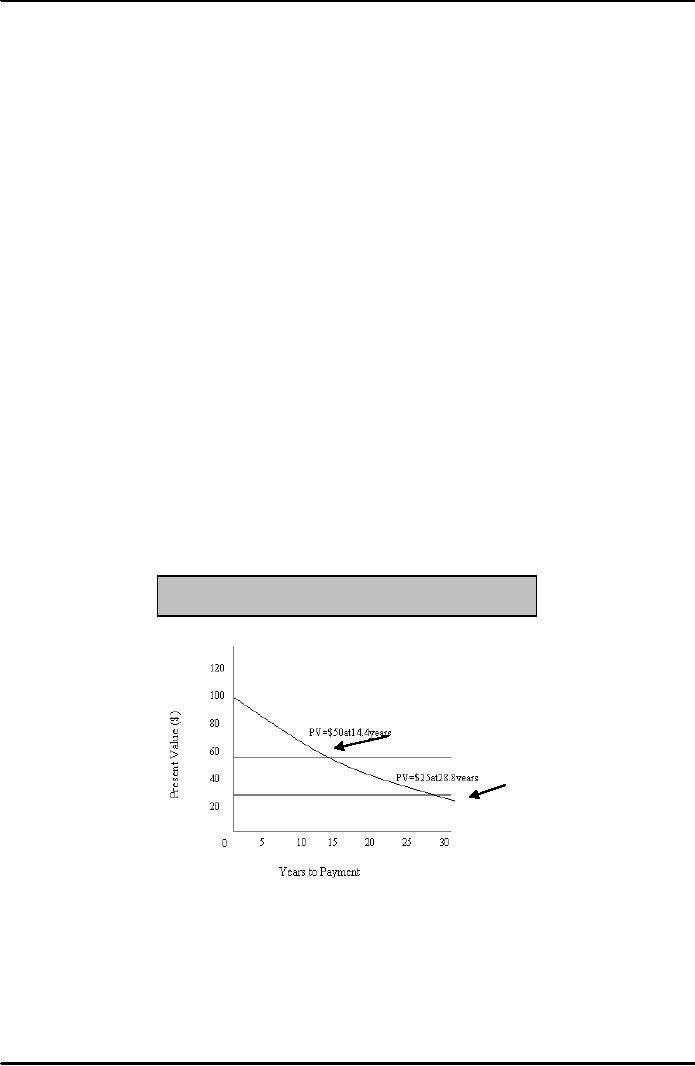
This
process shows us that the PV
payment is worth $100 if it is
made immediately, but
gradually
declines to $23 for a payment
made in 30 years
Figure:
Present value of $100 at 5%
interest rate
The
rule of 72
For
reasonable rates of return, the
time it takes to double the
money, is given approximately
by
t
= 72 / i%
If
we have an interest rate of 10%, the time it
takes for investment to
double is:
t
= 72 / 10 = 7.2 years
This
rule is fairly applicable to
discount rates in 5% to 20%
range.
25
Money
& Banking MGT411
VU
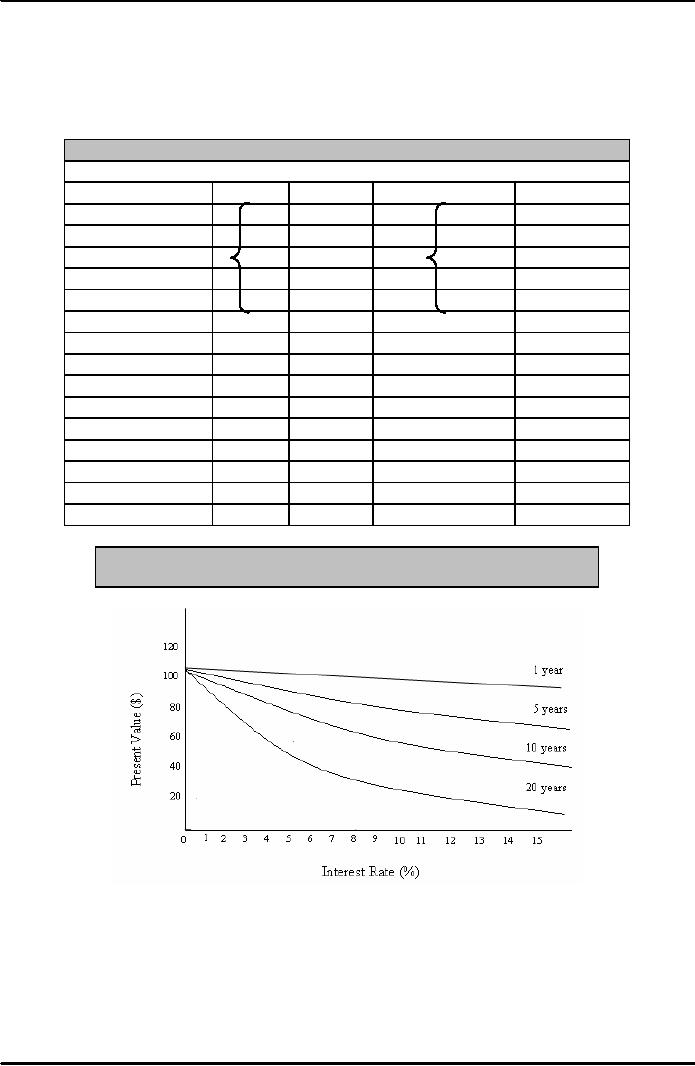
The
Interest rate (i)
Higher
interest rates are associated
with lower present values, no matter
what size or timing
of
the
payment
At
any fixed interest rate, an increase in
the time until a payment is
made reduces its
present
value
Table:
Present Value of a $100
payment
Payment
due in
Interest
rate
1
Year 5 Years
10
Years
20
Years
1%
$99.01
$95.15
$90.53
$81.95
2%
$3.77
$98.04
$90.57
$29.14
$82.03
$67.30
3%
4%
$97.09
$86.26
32%
$74.41
$55.37
4%
$96.15
$82.19
$67.56
$45.64
5%
$95.24
$78.35
$61.39
$37.69
6%
$94.34
$74.73
$55.84
$31.18
7%
$93.46
$71.30
$50.83
$25.84
8%
$92.59
$68.06
$46.32
$21.45
9%
$91.74
$64.99
$42.24
$17.84
10%
$90.91
$62.09
$38.55
$14.86
11%
$90.09
$59.35
$35.22
$12.40
12%
$89.29
$56.74
$32.20
$10.37
13%
$88.50
$54.28
$29.46
$8.68
14%
$87.72
$51.94
$26.97
$7.28
15%
$86.96
$49.72
$24.72
$6.11
Figure:
The relationship between Present
value and Interest
Rates
Compound
Annual Rates
Comparing
changes over days, months,
years and decades can be
very difficult.
The
way to deal with such
problems is to turn the monthly growth
rate into compound-annual
rate.
An
investment whose value grows
0.5% per month goes from
100 at the beginning of the
month
to
100.5 at the end of the month:
We
can verify this as
following
26

Money
& Banking MGT411
VU
100
(100.5 - 100) = [(100.5/100) 1] =
0.5%
100
What
if the investment's value continued to
grow at 0.5% per month for
next 12 months?
We
cant simply multiply 0.5 by
12
Instead
we need to compute a 12 month compound
rate
So
the future value of 100 at
0.5 %( 0.005) per month compounded
for 12 months will
be:
FVn = PV
(1+i) n
=
100(1.005)12
=
106.17
An
increase of 6.17% which is greater
than 6%, had we multiplied
0.5% by 12
The
difference between the two answers grows
as the interest rate grows
At
1% monthly rate, 12 month compounded rate
is12.68%
Another
use for compounding is to compute the
percentage change per year
when we know how
much
an investment has grown over
a number of years
This
rate is called average annual
rate
If
an investment has increased
20%, from 100 to 120
over 5 years
Is
average annual rate is simply
dividing 20% by 5?
This
way we ignore compounding
effect
Increase
in 2nd year must be calculated as
percentage of the investment worth at the
end of 1st
year
To
calculate the average annual rate, we
revert to the same
equation:
FVn = PV
(1+i) n
120
= 100(1 + i) 5
Solving
for i
i
= [(120/100)1/5 - 1] = 0.0371
5
consecutive annual increases of 3.71%
will result in an overall
increase of 20%
Interest
Rate and Discount Rate
The
interest rate used in the present value
calculation is often referred to as the
discount rate
because
the calculation involves discounting or
reducing future payments to
their equivalent
value
today.
Another
term that is used for the interest rate
is yield
Saving
behavior can be considered in terms of a
personal discount rate;
People
with a low rate are more
likely to save, while people
with a high rate are more
likely to
borrow
We
all have a discount rate
that describes the rate at which we
need to be compensated
for
postponing
consumption and saving our
income
If
the market offers an interest rate higher
than the individual's personal discount
rate, we would
expect
that person to save (and
vice versa)
Higher
interest rates mean higher
saving
Applying
Present Value
To
use present value in practice we
need to look at a sequence or
stream of payments
whose
present
values must be summed. Present
value is additive.
To
see how this is applied we
will look at internal rate of
return and the valuation of
bonds
Internal
Rate of Return
The
Internal Rate of Return is the interest
rate that equates the present
value of an investment
with
it cost.
It
is the interest rate at which the present
value of the revenue stream equals the
cost of the
investment
project.
27

Money
& Banking MGT411
VU
In
the calculation we solve for the interest
rate
A
machine with a price of $1,000,000
that generates $150,000/year
for 10 years
$
150 , 000
$
150 , 000
$
150 , 000
$
150 , 000
$
1, 000 , 000 =
+
+
+
......
+
(1
+
i
)
1
(1
+
i
)
2
(1
+
i
)
3
(1
+
i
)
10
Solving
for i, i=.0814 or
8.14%
The
internal rate of return must be
compared to a rate of interest that
represents the cost of
funds
to
make the investment.
These
funds could be obtained from
retained earnings or borrowing. In either
case there is an
interest
cost
An
investment will be profitable if
its internal rate of return
exceeds the cost of
borrowing
28
Table of Contents:
- TEXT AND REFERENCE MATERIAL & FIVE PARTS OF THE FINANCIAL SYSTEM
- FIVE CORE PRINCIPLES OF MONEY AND BANKING:Time has Value
- MONEY & THE PAYMENT SYSTEM:Distinctions among Money, Wealth, and Income
- OTHER FORMS OF PAYMENTS:Electronic Funds Transfer, E-money
- FINANCIAL INTERMEDIARIES:Indirect Finance, Financial and Economic Development
- FINANCIAL INSTRUMENTS & FINANCIAL MARKETS:Primarily Stores of Value
- FINANCIAL INSTITUTIONS:The structure of the financial industry
- TIME VALUE OF MONEY:Future Value, Present Value
- APPLICATION OF PRESENT VALUE CONCEPTS:Compound Annual Rates
- BOND PRICING & RISK:Valuing the Principal Payment, Risk
- MEASURING RISK:Variance, Standard Deviation, Value at Risk, Risk Aversion
- EVALUATING RISK:Deciding if a risk is worth taking, Sources of Risk
- BONDS & BONDS PRICING:Zero-Coupon Bonds, Fixed Payment Loans
- YIELD TO MATURIRY:Current Yield, Holding Period Returns
- SHIFTS IN EQUILIBRIUM IN THE BOND MARKET & RISK
- BONDS & SOURCES OF BOND RISK:Inflation Risk, Bond Ratings
- TAX EFFECT & TERM STRUCTURE OF INTEREST RATE:Expectations Hypothesis
- THE LIQUIDITY PREMIUM THEORY:Essential Characteristics of Common Stock
- VALUING STOCKS:Fundamental Value and the Dividend-Discount Model
- RISK AND VALUE OF STOCKS:The Theory of Efficient Markets
- ROLE OF FINANCIAL INTERMEDIARIES:Pooling Savings
- ROLE OF FINANCIAL INTERMEDIARIES (CONTINUED):Providing Liquidity
- BANKING:The Balance Sheet of Commercial Banks, Assets: Uses of Funds
- BALANCE SHEET OF COMMERCIAL BANKS:Bank Capital and Profitability
- BANK RISK:Liquidity Risk, Credit Risk, Interest-Rate Risk
- INTEREST RATE RISK:Trading Risk, Other Risks, The Globalization of Banking
- NON- DEPOSITORY INSTITUTIONS:Insurance Companies, Securities Firms
- SECURITIES FIRMS (Continued):Finance Companies, Banking Crisis
- THE GOVERNMENT SAFETY NET:Supervision and Examination
- THE GOVERNMENT'S BANK:The Bankers' Bank, Low, Stable Inflation
- LOW, STABLE INFLATION:High, Stable Real Growth
- MEETING THE CHALLENGE: CREATING A SUCCESSFUL CENTRAL BANK
- THE MONETARY BASE:Changing the Size and Composition of the Balance Sheet
- DEPOSIT CREATION IN A SINGLE BANK:Types of Reserves
- MONEY MULTIPLIER:The Quantity of Money (M) Depends on
- TARGET FEDERAL FUNDS RATE AND OPEN MARKET OPERATION
- WHY DO WE CARE ABOUT MONETARY AGGREGATES?The Facts about Velocity
- THE FACTS ABOUT VELOCITY:Money Growth + Velocity Growth = Inflation + Real Growth
- THE PORTFOLIO DEMAND FOR MONEY:Output and Inflation in the Long Run
- MONEY GROWTH, INFLATION, AND AGGREGATE DEMAND
- DERIVING THE MONETARY POLICY REACTION CURVE
- THE AGGREGATE DEMAND CURVE:Shifting the Aggregate Demand Curve
- THE AGGREGATE SUPPLY CURVE:Inflation Shocks
- EQUILIBRIUM AND THE DETERMINATION OF OUTPUT AND INFLATION
- SHIFTS IN POTENTIAL OUTPUT AND REAL BUSINESS CYCLE THEORY