 |
ORDERED PAIR:BINARY RELATION, BINARY RELATION |
| << BICONDITIONAL:UNION, VENN DIAGRAM FOR UNION |
| REFLEXIVE RELATION:SYMMETRIC RELATION, TRANSITIVE RELATION >> |

MTH001
Elementary Mathematics
LECTURE #
08
ORDERED
PAIR:
An
ordered pair (a, b) consists
of two elements "a" and
"b" in which "a" is
the
first
element
and "b" is the second
element.
The
ordered pairs (a, b) and
(c, d) are equal if,
and only if, a= c and b =
d.
Note
that (a, b) and (b, a)
are not equal unless a =
b.
EXERCISE:
Find
x and y given (2x, x + y) =
(6, 2)
SOLUTION:
Two
ordered pairs are equal if
and only if the
corresponding
components are equal. Hence,
we obtain the
equations:
2x
= 6 ..................(1)
and
x
+ y = 2 .................(2)
Solving
equation (1) we get x = 3
and when substituted in (2)
we get y = -1.
ORDERED
n-TUPLE:
The
ordered n-tuple, (a1,
a2, ..., an)
consists of elements a1,
a2, ..an
together
with the
ordering:
first a1,
second a2,
and so forth up to an. In
particular, an ordered 2-
tuple
is
called
an ordered pair, and an
ordered 3-tuple is called an
ordered
triple.
Two
ordered n-tuples (a1, a2,
..., an) and (b1, b2, ...,
bn) are equal if
and
only if each corresponding
pair of their elements is
equal, i.e., ai =
bj, for all
i
= 1, 2... n.
CARTESIAN
PRODUCT OF TWO
SETS:
denoted
A ◊
B
(read "A
Let
A and B be sets. The
Cartesian product of A and
B,
cross
B") is the set of all
ordered
pairs
(a, b), where a is in A and
b is in B.
Symbolically:
A
◊B
= {(a, b)| a ∈
A
and b ∈
B}
NOTE
A
◊B
has m
◊
n
If
set A has m
elements
and set B has
n
elements
then
elements.
EXAMPLE:
Let
A = {1, 2}, B = {a, b, c}
then
A
◊B
= {(1,a), (1,b), (1,c),
(2,a), (2, b), (2,
c)}
B
◊A
= {(a,1), (a,2), (b, 1),
(b, 2), (c, 1),
(c, 2)}
A
◊A
= {(1, 1), (1,2), (2,
1), (2, 2)}
B
◊B
= {(a, a), (a, b),
(a, c), (b, a),
(b, b), (b, c),
(c, a), (c, b),(c,
c)}
REMARK:
1.
A ◊
B≠B
◊
A
for non-empty and unequal
sets A and B.
2.
A ◊ φ
= φ ◊ A = φ
3.
| A ◊
B| = |A|
◊
|B|
CARTESIAN
PRODUCT OF MORE THAN TWO
SETS:
The
Cartesian product of sets
A1,
A2, ..., An,
denoted A1◊
A2 ◊
... ◊An,
is the set of
all
ordered n-tuples (a1,
a2, ..., an)
where a1 ∈A1,
a2 ∈A2,...,
an ∈An.
Symbolically:
A1◊
A2 ◊
... ◊An ={(a1, a2, ...,
an) | ai
∈Ai,
for i=1, 2, ..., n}
BINARY
RELATION:
Let
A and B be sets. A (binary)
relation R from A to B is a subset of A
◊
B.
When
(a, b) ∈R, we say a is
related to b by R, written a R b.
Otherwise
if (a, b) ∉R, we write a R
b.
EXAMPLE:
Page
36

MTH001
Elementary Mathematics
Let
A = {1, 2}, B = {1, 2,
3}
Then
A ◊
B =
{(1, 1), (1, 2),
(1, 3), (2, 1),
(2, 2), (2,
3)}
Let
R1={(1,1),
(1, 3), (2,
2)}
R2={(1,
2), (2, 1), (2,
2), (2, 3)}
R3={(1,
1)}
R4=
A ◊
B
R5=
∅
All
being subsets of A ◊
B
are relations from A to
B.
DOMAIN
OF A RELATION:
The
domain of a relation R from A to B is
the set of all first
elements of the
ordered
pairs which belong to R
denoted
Dom(R).
Symbolically:
Dom
(R) = {a ∈A| (a,b)
∈R}
RANGE
OF A RELATION:
The
range of A relation R from A to B is
the set of all
second
elements
of
the
ordered
pairs which belong to R
denoted
Ran(R).
Symbolically:
Ran(R)
= {b ∈B|(a,b)
∈
R}
EXERCISE:
Let
A
= {1, 2},
B
= {1, 2, 3},
Define
a binary relation R from A to B as
follows:
R
= {(a, b) ∈A ◊
B | a <
b}
Then
a.
Find the ordered pairs in
R.
b.
Find the Domain and
Range of R.
c.
Is 1R3, 2R2?
SOLUTION:
Given
A = {1, 2}, B = {1, 2,
3},
A
◊
B =
{(1,1), (1,2), (1,3), (2,1),
(2,2), (2,3)}
a.
R = {(a, b) ∈A ◊
B | a <
b}
R
= {(1,2), (1,3),
(2,3)}
b.
Dom(R) = {1,2} and Ran(R) =
{2, 3}
a.
Since (1,3) ∈R so
1R3
But
(2, 2) ∉R so 2 is not
related with3.
EXAMPLE:
Let
A = {eggs, milk, corn} and B
= {cows, goats, hens}
Define
a relation R from A to B by (a, b)
∈R
iff
a is produced by
b.
Then
R = {(eggs, hens), (milk,
cows), (milk, goats)}
Thus,
with respect to this
relation eggs R hens , milk
R cows, etc.
EXERCISE
:
Find
all binary relations from
{0,1} to {1}
SOLUTION:
Let
A = {0,1} &
B
= {1}
Then
A ◊
B =
{(0,1), (1,1)}
All
binary relations from A to B
are in fact all subsets
of
A
◊B,
which are:
R1=
∅
R2={(0,1)}
R3={(1,1)}
Page
37
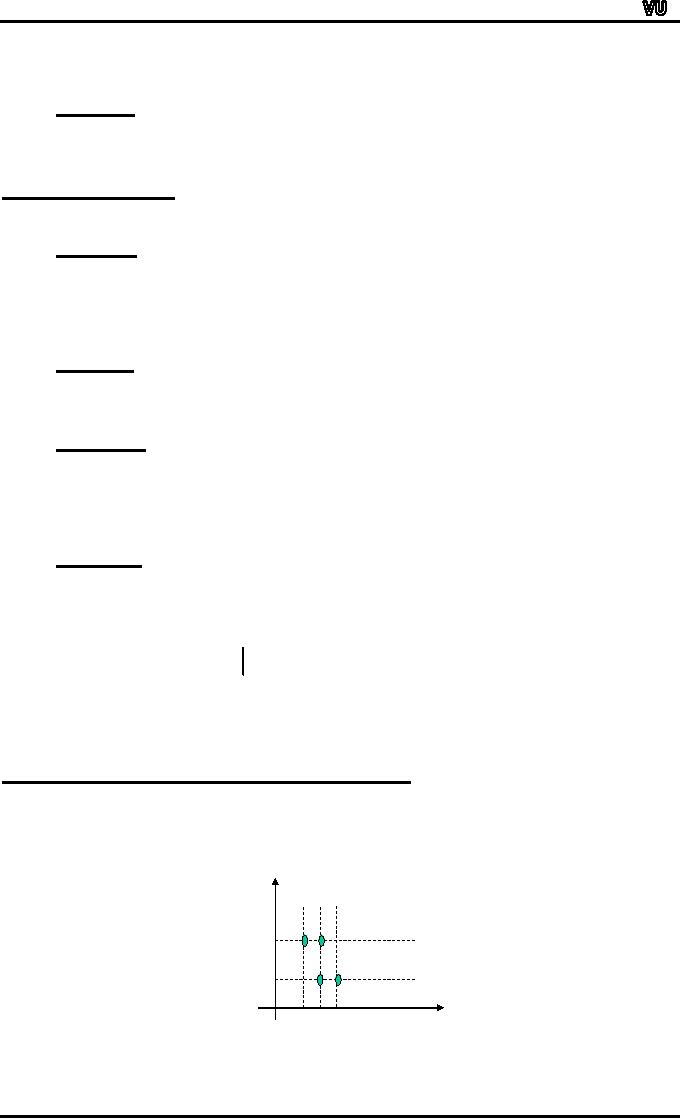
MTH001
Elementary Mathematics
R4={(0,1),
(1,1)} = A ◊
B
REMARK:
If
|A| = m and |B| = n
Then
as we know that the number
of elements in A ◊
B
are m ◊
n.
Now as we
m◊n
.
know
that the total number of
and the total number of
relations from A to B
are2
RELATION
ON A SET:
A
relation on the set A is a
relation from A to A.
In
other words, a relation on a
set A is a subset of A ◊
A.
EXAMPLE:
:
Let
A = {1, 2, 3, 4}
Define
a relation R on A as
(a,b)
∈
R
iff
a divides b
{symbolically written as a |
b}
Then
R = {(1,1), (1,2), (1,3),
(1,4), (2,2), (2,4),
(3,3),
(4,4)}
REMARK:
For
any set A
1.
A ◊
A is
known as the universal
relation.
2.
∅
is
known as the empty
relation.
EXERCISE:
Define
a binary relation E on the
set of the integers Z,
as
follows:
for
all m,n ∈Z, m E n ⇔
m n is
even.
Is
(6,6) ∈E? Is
(-1,7) ∈E?
a.
Is 0E0?
Is
5E2?
b.
Prove that for any
even integer n, nE0.
SOLUTION
E
= {(m,n) ∈Z ◊Z | m n is
even}
a.
(i) (0,0) ∈
Z ◊Z
and
0-0
= 0 is even
Therefore
0E0.
(5,2)
∈
Z ◊Z
but 5-2 = 3 is not
even
(ii)
so
5E2
(6,6)
∈
E
(iii)
since
6-6 = 0 is an even
integer.
(-1,7)
∈E
(iv)
since
(-1) 7 = -8 is an even
integer.
a.
For any even integer, n, we
have
n
0 = n,
an
even integer
so
(n, 0) ∈E
or
equivalently
n E 0
COORDINATE
DIAGRAM (GRAPH) OF A
RELATION:
Let
A = {1, 2, 3} and B = {x,
y}
Let
R be a relation from A to B defined
as
R
= {(1, y), (2, x),
(2, y), (3,
x)}
The
relation may be represented in a
coordinate diagram as
follows:
y
B
x
123
A
Page
38
MTH001
Elementary Mathematics
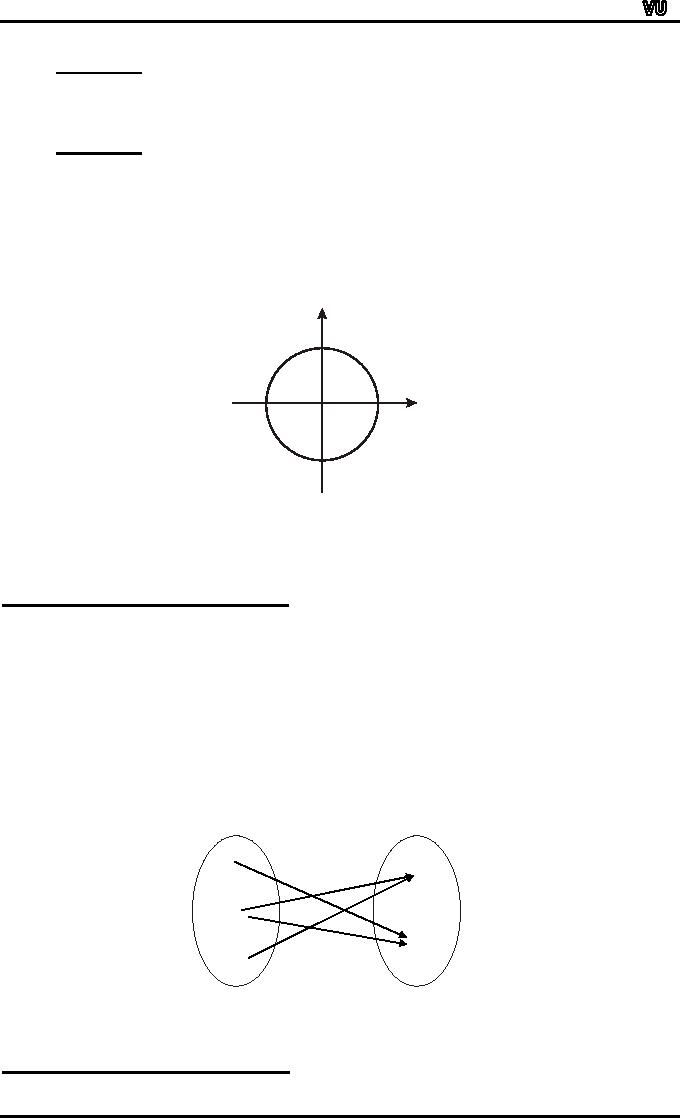
EXAMPLE:
Draw
the graph of the binary
relation C from R to
R
defined
as
follows:
(x,
y) ∈C
⇔
x2 + y2 =
1
for
all (x, y) ∈R ◊
R,
SOLUTION
x2+y2=1,
All
ordered pairs (x, y) in
relation C satisfies the
equation
which
when solved for y
gives
Clearly
y is real, whenever 1 ≤
x ≤ 1
Similarly
x is real, whenever 1 ≤
y ≤ 1
Hence
the graph is limited in the
range 1 ≤
x ≤ 1 and 1
≤
y ≤ 1
The
graph of relation is
y
(0,1)
(1,0)
(0,0)
(-1,0)
(0,-1)
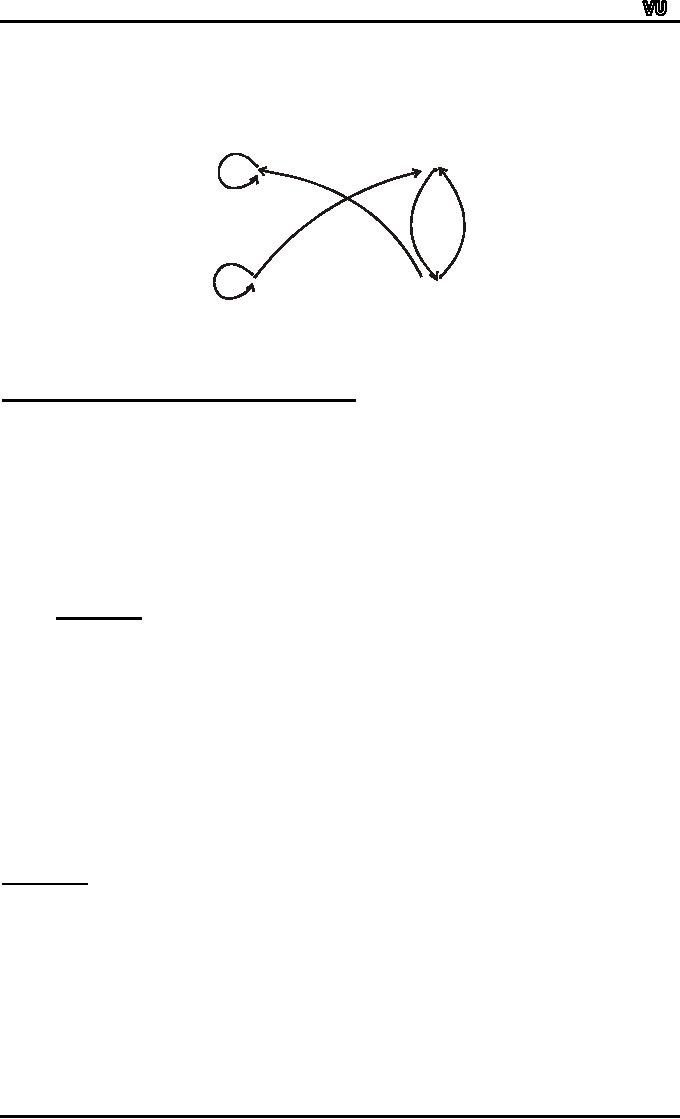
ARROW
DIAGRAM OF A RELATION:
Let
A
= {1, 2, 3}, B = {x, y}
and
R
= {1,y), (2,x), (2,y),
(3,x)}
be
a relation from A to B.
The
arrow diagram of R
is:
R
1
x
2
y
3
A
B
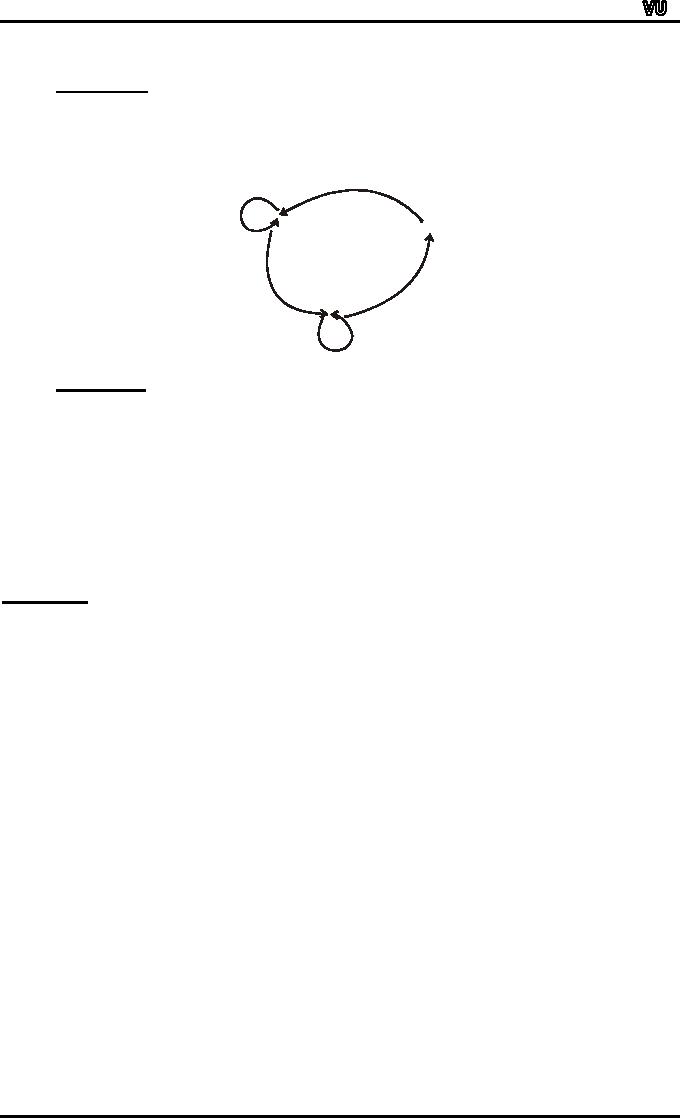
DIRECTED
GRAPH OF A RELATION:
Page
39
MTH001
Elementary Mathematics
Let
A = {0, 1, 2, 3}
and
R = {(0,0), (1,3), (2,1),
(2,2), (3,0), (3,1)}
be
a binary relation on A.
1
0
2
3
DIRECTED
GRAPH
MATRIX
REPRESENTATION OF A RELATION
Let
A
= {a1, a2, ..., an} and B =
{b1, b2, ..., bm}. Let R be
a
relation
from A to
B.
Define the n ◊
m
order matrix M by
⎧1 if
(ai , bi ) ∈
R
m(i,
j)
=
⎨
⎩0 if
(ai , bi ) ∉
R
for
i=1,2,...,n
and
j=1,2,...,m
EXAMPLE:
Let
A = {1, 2, 3} and B = {x,
y}
Let
R be a relation from A to B defined
as
R
={(1,y), (2,x), (2,y),
(3,x)}
x
y
1
⎡0
1⎤
M
=
2
⎢1
1⎥
⎢
⎥
3
⎢1
0⎥
3◊2
⎣
⎦
EXAMPLE:
For
the relation matrix.
1 2 3
1
⎡1
0 1⎤
M
=
2
⎢1
0 0⎥
⎢
⎥
3
⎢0
1 1⎥
⎣
⎦
1.
List the set of ordered
pairs represented by M.
2.
Draw the directed graph of
the relation.
Page
40
MTH001
Elementary Mathematics
SOLUTION:
The
relation corresponding to the
given Matrix is
R
= {(1,1), (1,3), (2,1),
(3,1), (3,2), (3,3)}
∑
And
its Directed graph is given
below
2
1
3
EXERCISE:
Let
A = {2, 4} and B = {6, 8,
10} and define relations R
and S
from
A to B as follows:
for
all (x,y) ∈A ◊
B, x R y
⇔
x |
y
for
all (x,y) ∈A ◊
B, x S y
⇔
y 4 =
x
State
explicitly which ordered
pairs are in A ◊
B, R, S,
R∪S
and R∩S.
SOLUTION
A
◊
B =
{(2,6), (2,8), (2,10),
(4,6), (4,8), (4,10)}
R
= {(2,6), (2,8), (2,10),
(4,8)}
S
= {(2,6), (4,8)}
R
∪
S =
{(2,6), (2,8), (2,10),
(4,8)}= R
R
∩
S =
{(2,6), (4,8)}= S
Page
41
Table of Contents:
- Recommended Books:Set of Integers, SYMBOLIC REPRESENTATION
- Truth Tables for:DE MORGANíS LAWS, TAUTOLOGY
- APPLYING LAWS OF LOGIC:TRANSLATING ENGLISH SENTENCES TO SYMBOLS
- BICONDITIONAL:LOGICAL EQUIVALENCE INVOLVING BICONDITIONAL
- BICONDITIONAL:ARGUMENT, VALID AND INVALID ARGUMENT
- BICONDITIONAL:TABULAR FORM, SUBSET, EQUAL SETS
- BICONDITIONAL:UNION, VENN DIAGRAM FOR UNION
- ORDERED PAIR:BINARY RELATION, BINARY RELATION
- REFLEXIVE RELATION:SYMMETRIC RELATION, TRANSITIVE RELATION
- REFLEXIVE RELATION:IRREFLEXIVE RELATION, ANTISYMMETRIC RELATION
- RELATIONS AND FUNCTIONS:FUNCTIONS AND NONFUNCTIONS
- INJECTIVE FUNCTION or ONE-TO-ONE FUNCTION:FUNCTION NOT ONTO
- SEQUENCE:ARITHMETIC SEQUENCE, GEOMETRIC SEQUENCE:
- SERIES:SUMMATION NOTATION, COMPUTING SUMMATIONS:
- Applications of Basic Mathematics Part 1:BASIC ARITHMETIC OPERATIONS
- Applications of Basic Mathematics Part 4:PERCENTAGE CHANGE
- Applications of Basic Mathematics Part 5:DECREASE IN RATE
- Applications of Basic Mathematics:NOTATIONS, ACCUMULATED VALUE
- Matrix and its dimension Types of matrix:TYPICAL APPLICATIONS
- MATRICES:Matrix Representation, ADDITION AND SUBTRACTION OF MATRICES
- RATIO AND PROPORTION MERCHANDISING:Punch recipe, PROPORTION
- WHAT IS STATISTICS?:CHARACTERISTICS OF THE SCIENCE OF STATISTICS
- WHAT IS STATISTICS?:COMPONENT BAR CHAR, MULTIPLE BAR CHART
- WHAT IS STATISTICS?:DESIRABLE PROPERTIES OF THE MODE, THE ARITHMETIC MEAN
- Median in Case of a Frequency Distribution of a Continuous Variable
- GEOMETRIC MEAN:HARMONIC MEAN, MID-QUARTILE RANGE
- GEOMETRIC MEAN:Number of Pupils, QUARTILE DEVIATION:
- GEOMETRIC MEAN:MEAN DEVIATION FOR GROUPED DATA
- COUNTING RULES:RULE OF PERMUTATION, RULE OF COMBINATION
- Definitions of Probability:MUTUALLY EXCLUSIVE EVENTS, Venn Diagram
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:ADDITION LAW
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:INDEPENDENT EVENTS