 |
Turing machine |
| << Decidablity, Parsing Techniques |
Theory of
Automata
(CS402)
Theory of
Automata
Lecture
N0. 45
Reading
Material
Introduction
to Computer Theory
Chapter
19
Summary
Turing
machine, examples, DELETE
subprogram, example, INSERT
subprogram, example.
Turing
machine
The
mathematical models (FAs, TGs, PDAs) that
have been discussed so far
can decide whether a string is
accepted
or not by them i.e. these
models are language
identifiers. However, there
are still some
languages
which
can't be accepted by them e.g.
there
does not exist any FA or TG or
PDA accepting any
non-CFLs.
Alan
Mathison Turing developed the
machines called Turing machines,
which accept some non-CFLs
as well,
in
addition to CFLs.
Definition
A Turing
machine (TM) consists of the
following
An
alphabet  of input
letters.
An input
TAPE partitioned into cells,
having infinite many
locations in one direction. The
input string is placed
on the
TAPE starting its first letter on
the cell i, the rest of
the TAPE is initially filled
with blanks (D's).
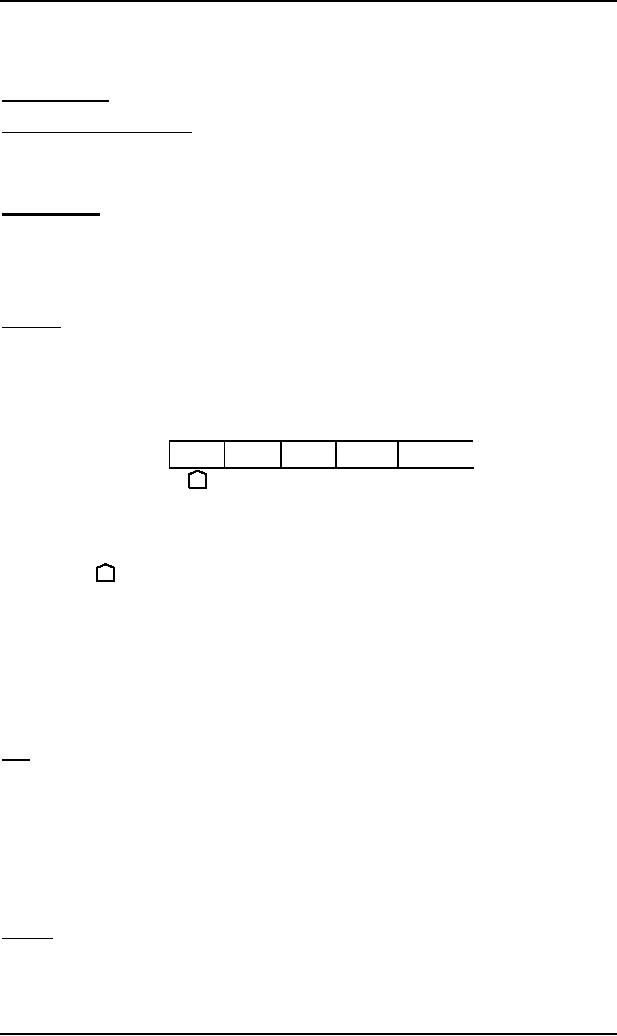
Input
TAPE
ii
iii
iv
i
D
µ
a
b
a
TAPE
Head
A tape
Head can read the
contents of cell on the TAPE
in one step. It can replace
the character at any cell
and
can
reposition itself to the next cell to
the right or to the left of
that it has just read.
Initially the TAPE Head is
at
the cell
i. The TAPE Head can't move
to the left of cell i. the
location of the TAPE Head is denoted
by
.
An
alphabet G of
characters that can be
printed on the TAPE by the
TAPE Head. G may
include the letters of Â.
Even
the TAPE Head can print
blank D, which
means to erase some
character from the
TAPE.
Finite
set of states containing exactly
one START state and
some (may be none) HALT states
that cause
execution
to terminate when the HALT
states are entered.
A program
which is
the set of rules, which show
that which state is to be
entered when a letter is read
form the
TAPE
and what character is to be printed. This
program is shown by the states
connected by directed edges
labeled by
triplet (letter, letter, direction). It
may be noted that the
first letter is the character
the TAPE Head
reads
from the cell to which it is
pointing. The second letter is
what the TAPE Head prints
the cell before it
leaves.
The direction tells the TAPE
Head whether to move one cell to the
right, R, or one cell to the
left, L.
Note
It may be
noted that there may not be
any outgoing edge at certain
state for certain letter to be read
from the
TAPE,
which creates nondeterminism in Turing
machines. It may also be
noted that at certain state,
there can't
be more
than one out going edges
for certain letter to be read from
the TAPE. The machine
crashes if there is
not
path for a letter to be read
from the TAPE and
the corresponding string is supposed to be
rejected.
To terminate
execution of certain input string
successfully, a HALT state
must be entered and the
corresponding
string is
supposed to be accepted by the
TM. The machine also
crashes when the TAPE Head
is instructed to
move
one cell to the left of cell
i.
Following
is an example of TM
Example
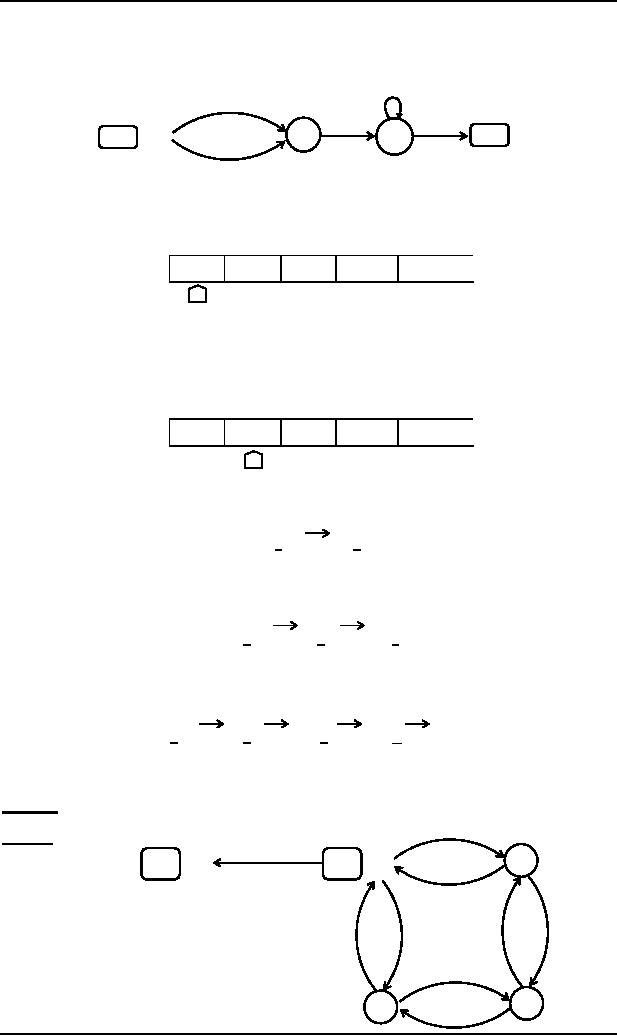
Consider
the following Turing
machine
147
Theory of
Automata
(CS402)
(a,a,R)
(b,b,R)
(a,a,R)
(D,D,R)
(b,b,R)
2
4
HALT
3
1
START
(b,b,R)
Let
the input string aba be run
over this TM
Input
TAPE
ii
iii
iv
i
D
µ
a
b
a
TAPE
Head
Starting
from the START state,
reading a form the TAPE and
according to the TM program, a will be
printed
i.e.
a
will be replaced by a and
the TAPE Head will be moved
one cell to the
right.
Which
can be seen as
Input
TAPE
ii
iii
iv
i
D
µ
a
b
a
TAPE
Head
This
process can be expressed
as
1
2
aba
aba
At state
2 reading b, state 3 is entered and
the letter b is replaced by b, i.e.
1
3
2
aba
aba
aba
At state
3 reading a, will keep the
state of the TM unchanged.
Lastly, the blank D is read
and D is
replaced by D
and
the HALT state is entered.
Which can be expressed
as
1
2
3
3
HALT
abaD
aba
aba
aba
Which
shows that the string aba is
accepted by this machine. It
can be observed, from the
program of the TM,
that
the machine accepts the
language expressed by
(a+b)b(a+b)*.
Theorem
Every
regular language is accepted by
some TM.
(b,b,R)
Example
(D,D,R)
2
1
START
5
HALT
(b,b,R)
(a,a,R)
(a,a,R)
(a,a,R)
(a,a,R)
(b,b,R)
4
3
(b,b,R)
148
Theory of
Automata
(CS402)
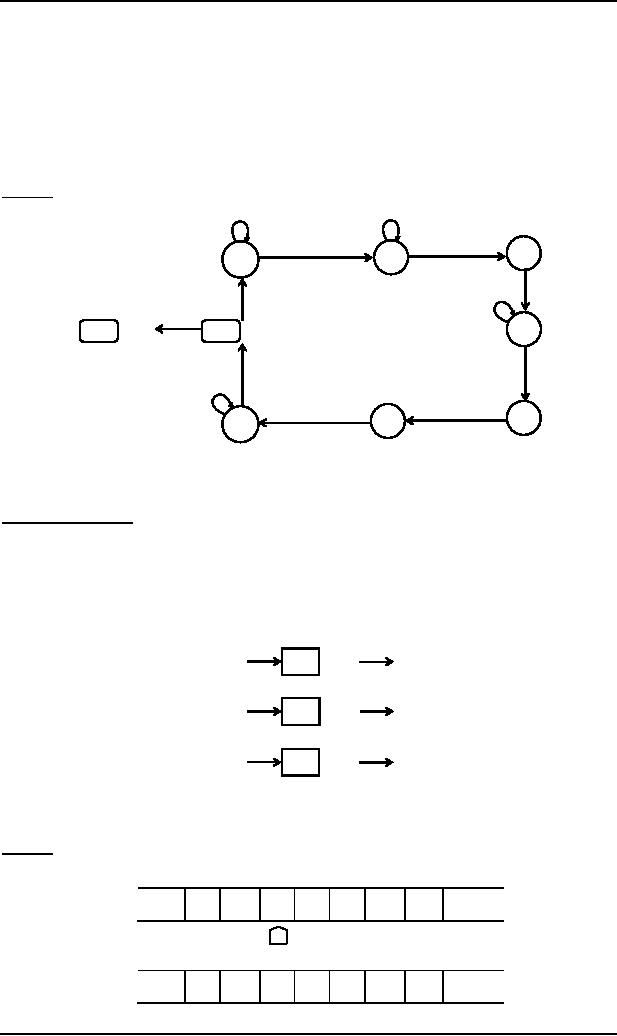
Consider
the EVEN-EVEN language.
Following is a TM accepting the
EVEN-EVEN language.
It may be
noted that the above diagram
is similar to that of FA corresponding to
EVEN-EVEN language.
Following
is another example
Example
Consider
the following TM
(b,b,R)
(a,a,R)
(a,a,L)
(b,b,R)
4
3
2
(b,a,R)
(a,*,R)
(a,a,R)
(D,D,R)
5
9
HALT
1
START
(D,D,L)
(*,*,R)
(a,a,L)
(b,b,L)
(a,D,L)
(a,D,L)
6
7
8
The
string aaabbbaaa can be observed to be
accepted by the above TM. It
can also be observed that
the above
TM
accepts the non-CFL {anbnan}.
INSERT
subprogram
Sometimes,
a character is required to be inserted on
the TAPE exactly at the
spot where the TAPE Head
is
pointing,
so that the character
occupies the required cell
and the other characters on
the TAPE are moved
one
cell
right. The characters to the
left of the pointed cell are
also required to remain as
such.
In the
situation stated above, the part of TM
program that executes the
process of insertion does not affect
the
function
that the TM is performing.
The subprogram of insertion is independent
and can be incorporated at
any
time with
any TM program specifying what character
to be inserted at what location. The subprogram
of
insertion
can be expressed as
INSERT
a
INSERT
b
INSERT
#
The
above diagrams show that the
characters a,b and # are to
be inserted, respectively. Following is an
example
showing
how does the subprogram
INSERT perform its
function
Example
If the
letter b is inserted at the cell where
the TAPE Head is pointing as
shown below
Dµ
µ
D
b
X
a
b
b
X
then, it
is expressed as
Dµ
µ
D
b
X
a
b
b
X
149
Theory of
Automata
(CS402)
INSERT
b
The
function of subprogram INSERT b can be
observed from the following
diagram
Dµ
µ
D
b
X
b
a
b
b
X
Following
is the INSERT subprogram
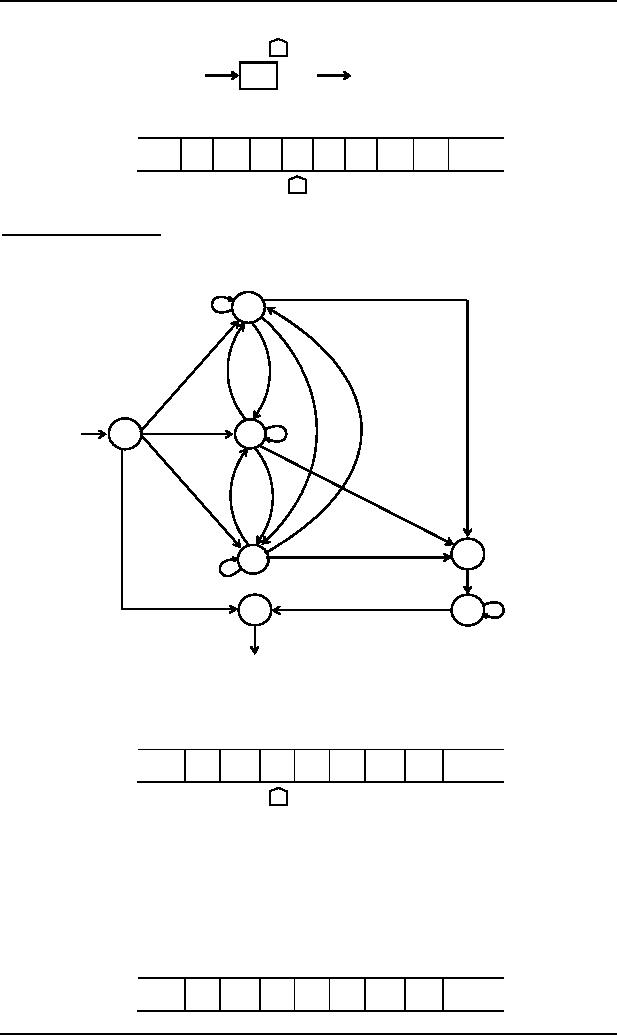
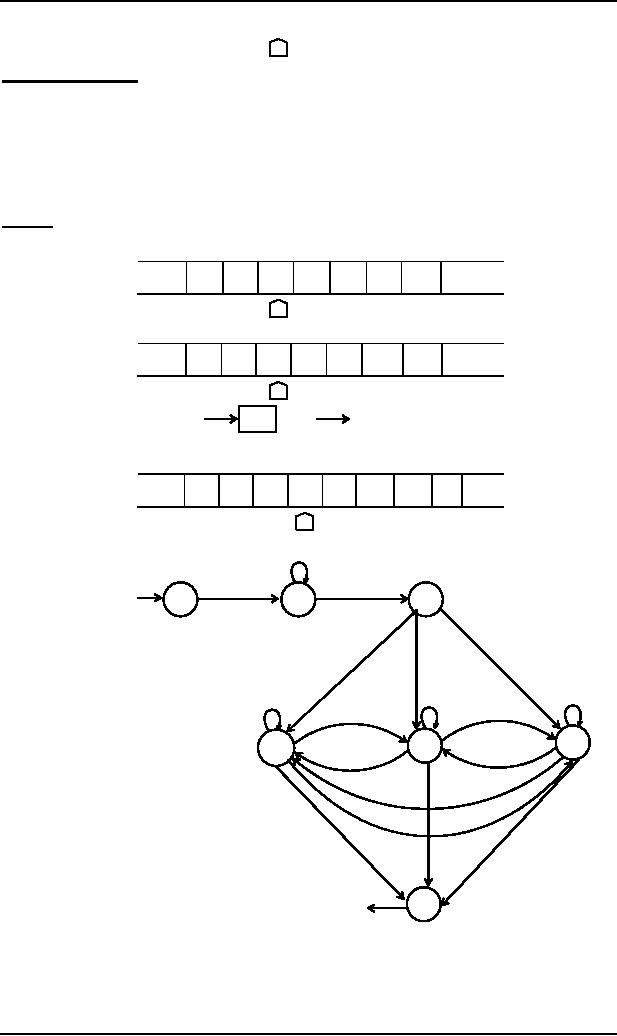
The
subprogram INSERT
Keeping
in view the same example of
inserting b at specified location, to determine the
required subprogram,
first Q
will be inserted as marker at the
required location, so that the
TAPE Head must be able to
locate the
proper
cell to the right of the insertion cell.
The whole subprogram INSERT is
given as
(a,a,R)
2
(a,Q,R)
(b,a,R)
(a,b,R)
(D,a,R)
(b,b,R)
(b,Q,R)
(a,X,R)
1
3
In
(X,a,R)
(b,X,R)
(D,
b,R)
(X,b,R)
(X,Q,R)
(D,
X,R)
5
4
(D,
b,R)
(D, D,L)
(X,X,R)
(b,b,L)
(Q,
b,R)
(a,a,L)
6
7
(X,X,L)
Out
It is
supposed that machine is at
state 1, when b is to be inserted.
All three possibilities of reading a, b or X
are
considered
by introducing the states
2,3 and 4 respectively. These
states remember what letter displaced
during
the
insertion of Q.
Consider
the same location where b is to be
inserted
Dµ
µ
D
b
X
a
b
b
X
After
reading a from the TAPE, the
program replaces a by Q and
the TAPE Head will be moved
one step right.
Here the
state 2 is entered. Reading b at state 2,
b will be replaced by a and
state 3 will be entered. At
state 3, b
is read
which is not replaced by any character
and the state 3 will not be
left.
At state
3, the next letter to be read is X,
which will be replaced by b
and the state 4 will be
entered. At state 4,
D will be
read, which will be replaced
by X and state 5 will be
entered. At state 5, D will be
read and without
any
change state 6 will be
entered, while TAPE Head
will be moved one step
left. The state 6 makes no
change
whatever
(except Q) is read at that
state. However at each step,
the TAPE Head is moved one
step left. Finally,
Q is read
which is replaced by b and
the TAPE Head is moved to
one step right.
Hence,
the required situation of the
TAPE can be shown as
Dµ
µ
D
b
X
a
b
b
X
150
Theory of
Automata
(CS402)
DELETE
subprogram
Sometimes,
a character is required to be DELETED on
the TAPE exactly at the
spot where the TAPE Head
is
pointing,
so that the other characters on
the right of the TAPE Head
are moved one cell
left. The characters
to
the
left of the pointed cell are
also required to remain as
such.
In the
situation stated above, the part of TM
program that executes the
process of deletion does not affect
the
function
that the TM is performing.
The subprogram of deletion is independent and
can be incorporated at any
time with
any TM program specifying what character
to be deleted at what location. The subprogram of
deletion
can be
expressed as
Example
If the
letter a is to be deleted from the string
bcabbc, shown below
Dµ
µ
D
b
c
a
b
b
c
then, it
is expressed as
Dµ
µ
D
b
c
a
b
b
X
DELETE
The
function of subprogram DELETE can be
observed from the following
diagram
µ
◊
◊◊
D
D
b
c
b
b
c
(a,a,R)
(b,b,R)
(c,c,R)
In
2
3
1
(c,D,R)
(D,D,L)
(b,D,R)
(a,D,R)
(c,D,L)
Following
is the DELETE subprogram
(b,
D,L)
(c,c,L)
(a,a,L)
(b,b,L)
(b,a,L)
(c,b,L)
6
5
4
(b,c,L)
(a,b,L)
(a,c,L)
(c,a,L)
(D,c,R)
(D,a,R)
(D,b,R)
Out
7
151

Theory of
Automata
(CS402)
The
process of deletion of letter a from the
string bcabbc can easily be
checked, giving the TAPE
situation as
shown
below
µ
◊
◊◊
D
D
b
c
b
b
c
152
Table of Contents:
- What does automata mean, Introduction to languages
- Kleene Star Closure, Recursive definition of languages
- Regular Expression, Recursive definition of Regular Expression
- Equivalent Regular Expressions
- Finite Automaton
- Equivalent FAs
- FA corresponding to finite languages
- Examples of TGs: accepting all strings
- Generalized Transition Graphs
- Nondeterminism, Kleene’s Theorem
- Proof(Kleene’s Theorem Part II)
- Kleene’s Theorem Part III
- Concatenation of FAs
- Closure of an FA
- Nondeterministic Finite Automaton, Converting an FA to an equivalent NFA
- NFA with Null String
- NFA and Kleene’s Theorem
- NFA corresponding to Concatenation of FAs
- Distinguishable strings and Indistinguishable strings
- Finite Automaton with output, Moore machine
- Mealy machine
- Equivalent machines
- Mealy machines in terms of sequential circuit
- Regular languages, Complement of a language
- Nonregular languages
- Pumping Lemma
- Pumping Lemma version II
- Pseudo theorem
- Decidability
- finiteness of a language
- Context Free Grammar (CFG), CFG terminologies
- Trees
- Polish Notation (o-o-o)
- Total language tree, Regular Grammar
- Null Production
- Chomsky Normal Form (CNF)
- A new format for FAs
- Nondeterministic PDA
- PDA corresponding to CFG
- Conversion form of PDA
- Conversion Form, Joints of the machine
- Row language, Nonterminals
- Non-Context-Free language, Pumping lemma for CFLs
- Decidablity, Parsing Techniques
- Turing machine