Trees

<< Context Free Grammar (CFG), CFG terminologies

Polish Notation (o-o-o) >>

Theory of Automata

(CS402)

Theory of Automata

Lecture N0. 32

Reading Material

Introduction to Computer Theory

Chapter 12

Summary

Examples of CFL, EVEN-EVEN, EQUAL, Language of strings containing bbb,

PALINDROME, {anbn}, Language of strings beginning and ending in different letters,

Parsing tree, example

Example

Â = {a,b}

productions:

S Æ SS

S Æ XS

SÆL

S Æ YSY

X Æ aa

X Æ bb

Y Æ ab

Y Æ ba

This grammar generates EVEN-EVEN language.

Example

Â = {a,b}

productions:

S Æ aB

S Æ bA

AÆa

A Æ aS

A Æ bAA

BÆb

B Æ bS

B Æ aBB

This grammar generates the language EQUAL(The language of strings, with number of a's equal to number of

b's).

Note

It is to be noted that if the same non-terminal have more than one productions, it can be written in single line

e.g. S Æ aS, S Æ bS, S Æ L can be written as S Æ aS|bS|L

It may also be noted that the productions S Æ SS|L always defines the language which is closed w.r.t.

concatenation i.e.the language expressed by RE of type r*. It may also be noted that the production S Æ SS

defines the language expressed by r+.

Example

Â = {a,b}

productions:

S Æ YXY

Y Æ aY|bY|L

X Æ bbb

It can be observed that, using prod.2, Y generates L. Y generates a. Y generates b. Y also generates all the

combinations of a and b. thus Y generates the strings generated by (a+b). It may also be observed that the above

Theory of Automata

(CS402)

CFG generates the language expressed by (a+b)*bbb(a+b)*. Following are four words generated by the given

CFG

fi YXY

S fi YXY

fi bYbbbaY

fi aYbbbL

fi bLbbbabY

fi abYbbb

fi bbbbabbY

fi abLbbb

fi bbbbabbaY

= abbbb

fi bbbbabbaL

= bbbbabba

S fi

fi YXY

YXY

LbbbaY

fi bYbbbaY

fi bLbbbaL

bbbabY

= bbbba

bbbabaY

bbbabaL

bbbaba

Example

Consider the following CFG

S Æ SS|XaXaX|L

X Æ bX|L

It can be observed that, using prod.2, X generates L. X generates any number of b's. Thus X generates the

strings generated by b*. It may also be observed that the above CFG generates the language expressed by

(b*ab*ab*)*.

Example

Consider the following CFG

Â = {a,b}

productions:

S Æ aSa|bSb|a|b|L

The above CFG generates the language PALINDROME. It may be noted that the CFG

S Æ aSa|bSb|a|b generates the language NON-NULLPALINDROME.

Example

Consider the following CFG

Â = {a,b}

productions:

S Æ aSb|ab|L

It can be observed that the CFG generates the language {anbn: n = 0,1,2,3, ...}. It may also be noted that the

language {anbn: n=1,2,3, ...} can be generated by the CFG, S Æ aSb|ab

Example

Consider the following CFG

S Æ aXb|bXa

X Æ aX|bX|L

The above CFG generates the language of strings, defined over Â={a,b}, beginning and ending in different

letters.

Trees

As in English language any sentence can be expressed by parse tree, so any word generated by the given CFG

can also be expressed by the parse tree, e.g. consider the following CFG

S Æ AA

A Æ AAA|bA|Ab|a

Obviously, baab can be generated by the above CFG. To express the word baab as a parse tree, start with S.

Replace S by the string AA, of nonterminals, drawing the downward lines from S to each character of this string

as follows

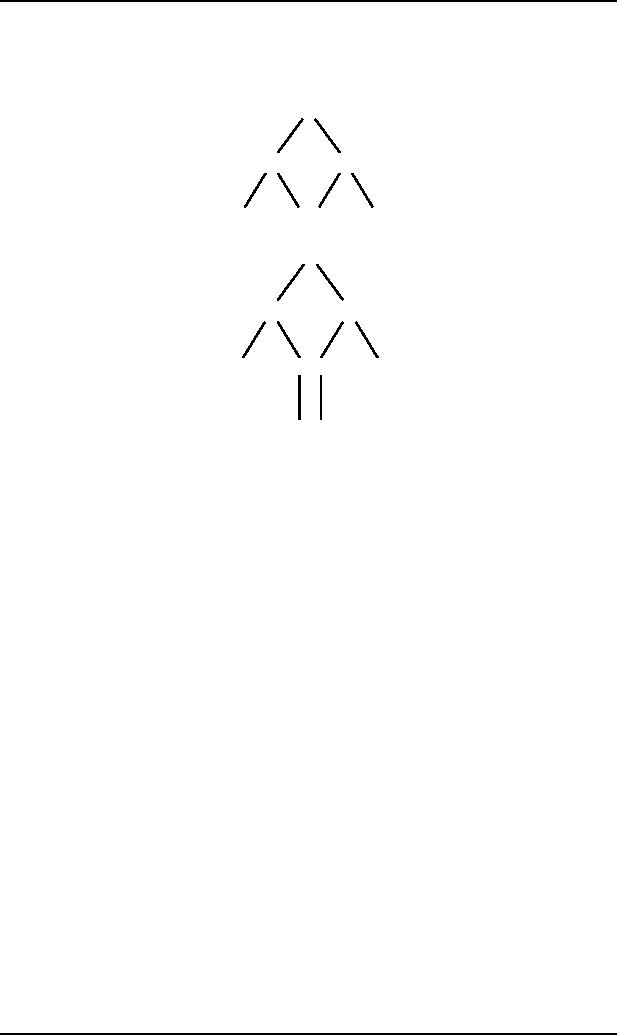
Theory of Automata

(CS402)

Now let the left A be replaced by bA and the right one by Ab then the tree will be

Replacing both A's by a, the above tree will be

Thus the word baab is generated. The above tree to generate the word baab is called Syntax tree or Generation

tree or Derivation tree as well.

Table of Contents: