TAX EFFECT & TERM STRUCTURE OF INTEREST RATE:Expectations Hypothesis

<< BONDS & SOURCES OF BOND RISK:Inflation Risk, Bond Ratings

THE LIQUIDITY PREMIUM THEORY:Essential Characteristics of Common Stock >>

Money & Banking MGT411

Lesson 17

TAX EFFECT & TERM STRUCTURE OF INTEREST RATE

Tax Effect

Term Structure of Interest Rate

Expectations Hypothesis

Liquidity Premium

Tax Effect

The second important factor that affects the return on a bond is taxes

Bondholders must pay income tax on the interest income they receive from privately issued

bonds (taxable bonds), but government bonds are treated differently

Interest payments on bonds issued by state and local governments, called "municipal" or "tax-

exempt" bonds are specifically exempt from taxation

A tax exemption affects a bond's yield because it affects how much of the return the bondholder

gets to keep

Tax-Exempt Bond Yield = (Taxable Bond Yield) x (1- Tax Rate).

Term Structure of Interest Rates

The relationship among bonds with the same risk characteristics but different maturities is

called the term structure of interest rates.

A plot of the term structure, with the yield to maturity on the vertical axis and the time to

maturity on the horizontal axis, is called the yield curve.

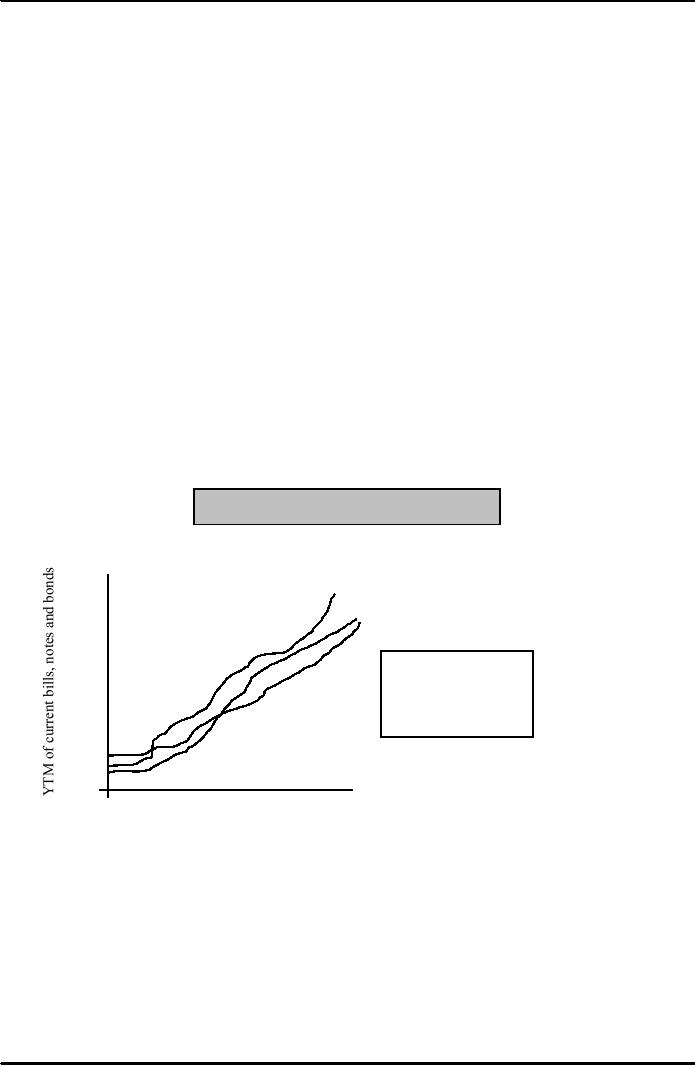
Figure: The U.S. Treasury Yield Curve

___Yesterday

6.0%

___1 month ago

___1 year ago

5.0

The figure plots the

4.0

yields on Treasury

bills and bonds for

3.0

August 27, 2004.

2.0

1.0

Months

Years

________ Maturity________

Money & Banking MGT411

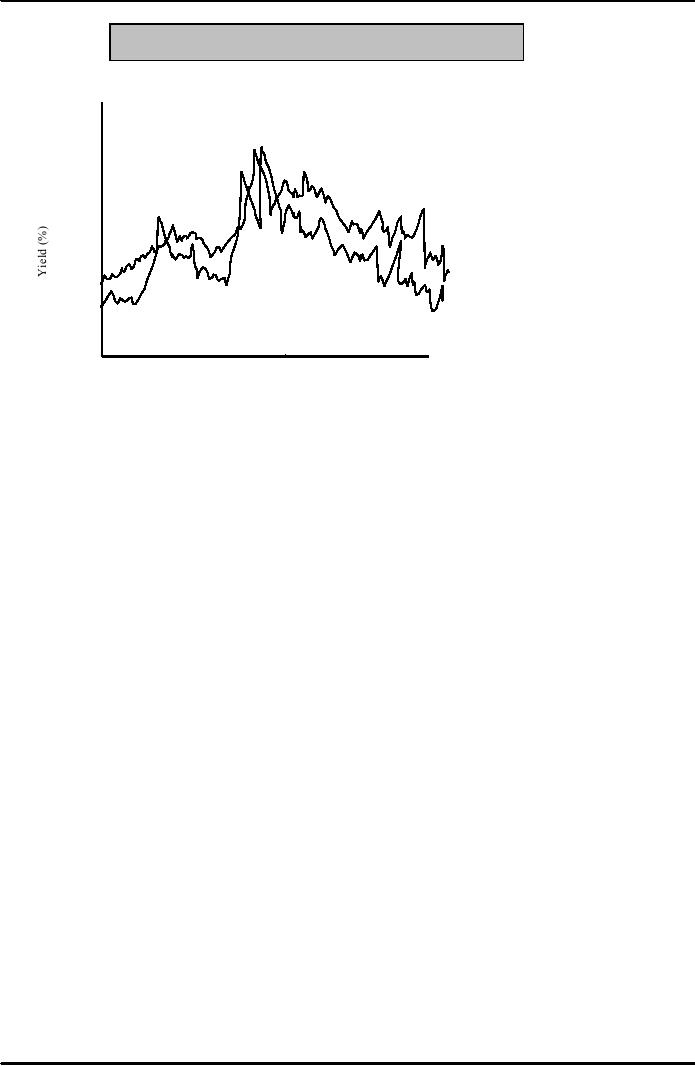
Figure: The Term Structure of Treasury Interest Rates

1979

1983

1987

1991 1995 1999

1971 11975

2003

___3 months T.Bills_____10 years T-Bonds

Term Structure "Facts"

Interest Rates of different maturities tend to move together

Yields on short-term bond are more volatile than yields on long-term bonds

Long-term yields tend to be higher than short-term yields.

Expectations Hypothesis

The risk-free interest rate can be computed, assuming that there is no uncertainty about the

future

Since certainty means that bonds of different maturities are perfect substitutes for each other, an

investor would be indifferent between holding

A two-year bond or

A series of two one-year bonds

Certainty means that bonds of different maturities are perfect substitutes for each other

Assuming that current 1-year interest rate is 5%. The expectations hypothesis implies that the

current 2-year interest rate should equal the average of 5% and 1-year interest rate one year in

future.

If future interest rate is 7%, then current 2-year interest rate will be (5+7) / 2 = 6%

Therefore, when interest rates are expected to rise long-term rates will be higher than short-term

rates and the yield curve will slope up (and vice versa)

Money & Banking MGT411

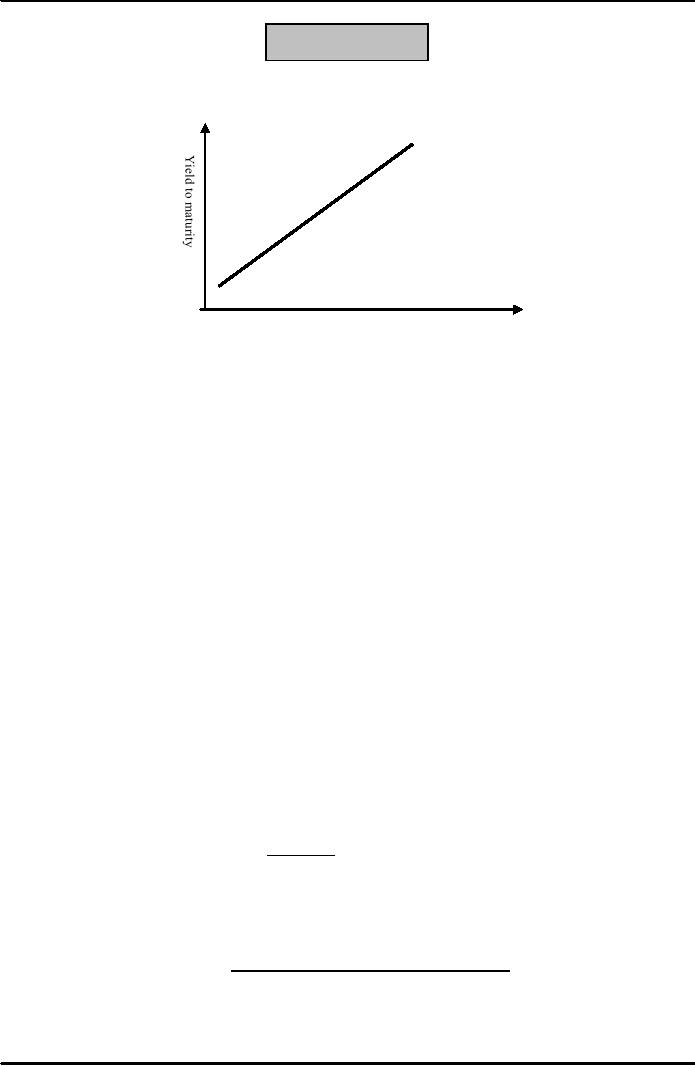
Figure: Yield Curve

Yield curve when interest rates are expected to

rise

Time to maturity

From this we can construct investment strategies that must have the same yield.

Assuming the investor has a two-year horizon, the investor can:

Invest in a two-year bond and hold it to maturity

Interest rate will be i2y

Investment will yield (1 + i2y) (1 + i2y) two years later

Invest in a one-year bond today and a second one a year from now when the first one matures

Interest rate will be iey+1

Investment will yield (1 + i1y) (1 + iey+1) in two years

The hypothesis tells us that investors will be indifferent between the two strategies, so the

strategies must have the same return

Total return from 2 year bonds over 2 years

(1 + i 2y )(1 + i 2y )

Return from one year bond and then another one year bond

(1 + i 1y )(1 + i 1y )

If one and two year bonds are perfect substitutes, then:

(1 + i 2y )(1 + i 2y ) = (1 + i 1y )(1 + 1y )

i1y + i1y

i 2y =

Or in general terms

i1 t + i1et + 1 + i1et + 2 + .... + i1et + n - 1

i nt

Therefore the rate on the two-year bond must be the average of the current one-year rate and the

expected future one-year rate

Money & Banking MGT411

Implications would be the same old

Interest rates of different maturities tend to move together.

Yields on short-term bonds are more volatile than those on long-term bonds.

Long-term yields tend to be higher than short-term yields

However, expectations theory can not explain why long-term rates are usually above short term

rates

In order to explain why the yield curve normally slopes upward, we need to extend the

hypothesis to include risk

Table of Contents: