 |
RELATIONS AND FUNCTIONS:FUNCTIONS AND NONFUNCTIONS |
| << REFLEXIVE RELATION:IRREFLEXIVE RELATION, ANTISYMMETRIC RELATION |
| INJECTIVE FUNCTION or ONE-TO-ONE FUNCTION:FUNCTION NOT ONTO >> |

MTH001
Elementary Mathematics
LECTURE #
11
RELATIONS AND
FUNCTIONS:
A
function F
from a
set X to a set Y is a relation
from X to Y that satisfies
the following two
properties
1.For
every element x in X, there is an
element y in Y such that
(x,y) ∈F.
In
other words every element of
X is the first element of
some ordered pair of
F.
2.For
all elements x in X and y
and z in Y, if (x,y) ∈F and
(x,z) ∈F, then y =
z
In
other words no two distinct
ordered pairs in F have the
same first element.
EXERCISE:
Which
of the relations define
functions from X = {2,4,5} to
Y={1,2,4,6}.
a.
R1
= {(2,4), (4,1)}
b.
R2
= {(2,4), (4,1), (4,2),
(5,6)}
c.
R3
= {(2,4), (4,1),
(5,6)}
SOLUTION
:
a.
R1 is not a function, because 5
∈X
does not appear as the
first element in any
ordered
pair
in R1.
b.
R2 is not a function, because
the ordered pairs (4,1)
and (4,2) have the
same first
element
but different second
elements.
c.
R3 defines a function because it
satisfy both the conditions
of the function that is
every
element
of X is the first element of
some order pair and
there is no pair which has
the same
first
order pair but different
second order pair.
EXERCISE:
Let
A = {4,5,6} and B = {5,6}
and define binary relations
R and S from A to B as
follows:
for
all (x,y) ∈A ×
B,
(x,y) ∈
R ⇔ x≥y
for
all (x,y) ∈A ×
B,
xSy
⇔
2|(x-y)
a.
Represent R and S as a set of
ordered pairs.
b.
Indicate whether R or S is a
function
SOLUTION:
Since
we are given the relation R
contains those order pairs
of A ×
B
which has their
first
element
greater or equal to the
second Hence R contains the
order pairs.
R
= {(5,5), (6,5),
(6,6)}
Similarly
S is such a relation which
consists of those order
pairs for which the
difference of
first
and second elements
difference divisible by 2.
Hence
S = {(4,6), (5,5),
(6,6)}
b.
R is not a function because 4
∈A
is not related to any
element of B.
S
clearly defines a function
since each element of A is
related to a unique element of
B.
FUNCTION:
A
function f
from a
set X to a set Y is a relationship
between
elements of X and elements
of
Y
such that each
element of X is
related to a unique
element of Y,
and is denoted f
: X →Y.
The
set X is called the domain
of f
and Y is
called the co-domain of
f.
NOTE:The
unique element y of Y that is
related to x by f
is denoted
f(x)
and is called
f
of x, or the
value of f
at x, or the
image of x under f
ARROW
DIAGRAM OF A FUNCTION:
The
definition of a function implies
that the arrow diagram
for a function f has the
following
two
properties:
1.
Every
element of X has an arrow
coming out of it
2.
No two
elements of X has two arrows
coming out of it that point
to two different
elements
of
Y.
EXAMPLE:
Page
58
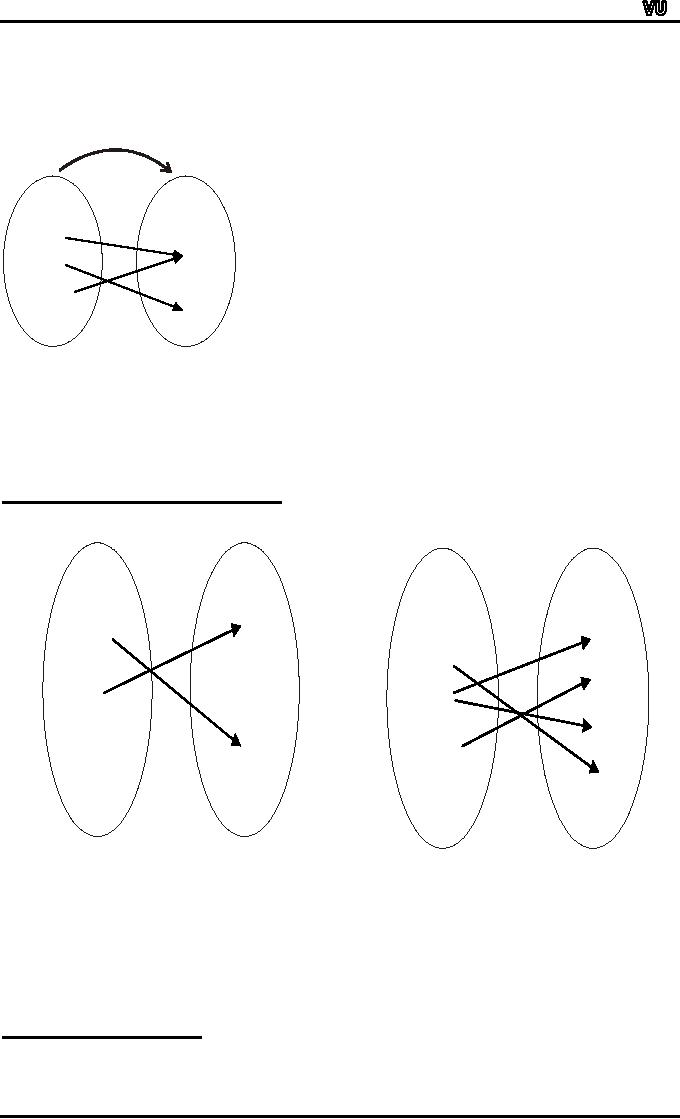
MTH001
Elementary Mathematics
Let
X = {a,b,c} and
Y={1,2,3,4}.
Define
a function f
from X to Y by
the arrow diagram.
f
.1
a.
.2
b.
.3
c.
.4
Y
X
You
can easily note that
the above diagram satisfy
the two conditions of a
function hence a
graph
of the function.
Note
that
f(a)
= 2, f(b) = 4,and f(c) =
2
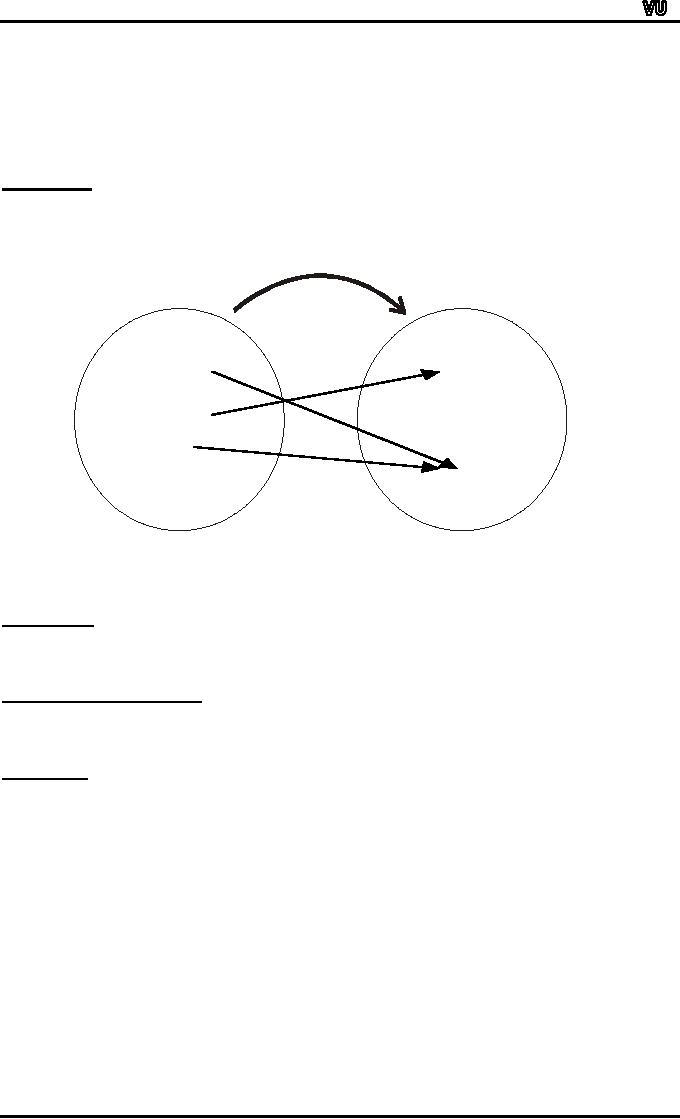
FUNCTIONS
AND NONFUNCTIONS:
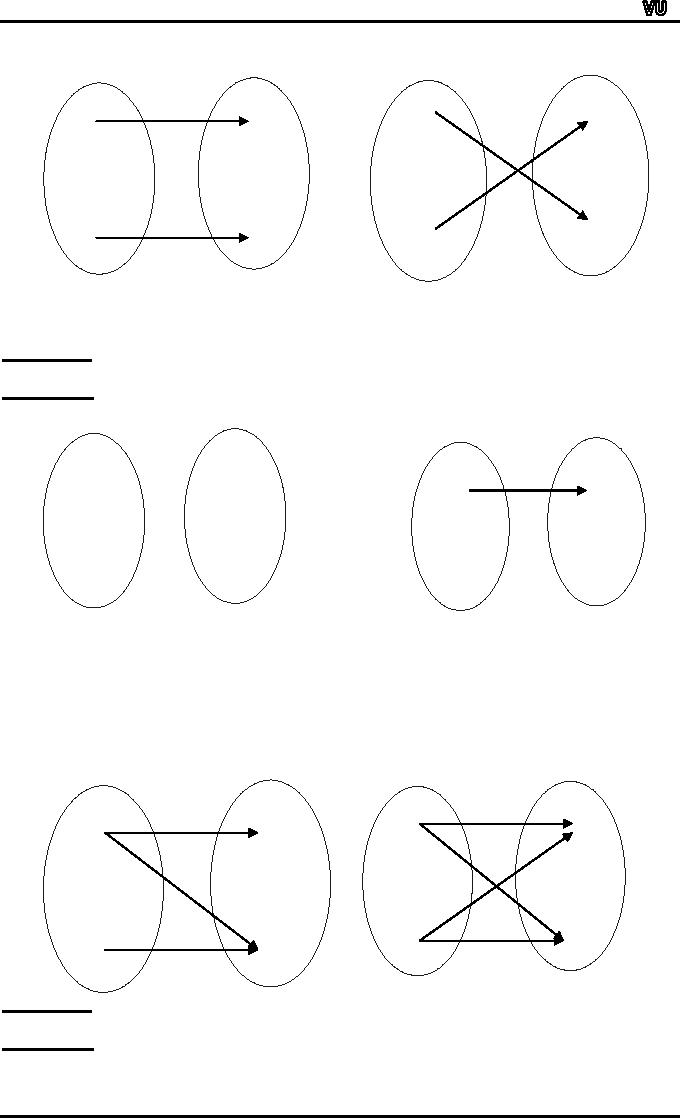
Which
of the arrow diagrams define
functions from X = {2,4,5}to Y =
{1,2,4,6}.
a.
b.
.1
.1
2.
2.
.2
.2
4.
4.
.4
.4
5.
5.
.6
.6
X
Y
X
Y
The
relation given in the
diagram (a) is Not
a function because
there is no arrow
coming
out
of of 5∈X
to any element of Y.
The
relation in the diagram (b)
is Not a
function, because
there are two arrows
coming out
of
4∈X.
i.e.,4∈X is not
related to a unique element of
Y.
RANGE
OF A FUNCTION:
Let
f: X→Y.
The range of f consists of
those elements of Y that are
image of elements of X.
Symbolically:
Range
of f = {y ∈Y| y = f(x),
for some x ∈X}
Page
59
MTH001
Elementary Mathematics
NOTE:
1.
The
range of a function f is always a
subset of the co-domain of
f.
The
range of f: X →Y is also
called the image of X under
f.
2.
3.
When
y = f(x), then x is called
the pre-image of y.
The
set of all elements of X,
that are related to some y
∈Y
is called the inverse
4.
image
of y.
EXERCISE:
Determine
the range of the functions
f, g, h from X = {2,4,5} to Y = {1,2,4,6}
defined as:
f
1.
X
Y
.
1
2.
.
2
4.
.
4
5.
.
6
2.
g
= {(2,6), (4,2),
(5,1)}
3.
h(2)
= 4,
h
(4) = 4,
h(5)
= 1
SOLUTION:
1.
Range of f =
{1, 6}
2.
Range of g =
{1, 2, 6}
3.
Range of h =
{1, 4}
GRAPH
OF A FUNCTION:
Let
f be a real-valued function of a real
variable. i.e. f:R →R. The
graph of f is the set of
all
points
(x,y) in the Cartesian
coordinate plane with the
property that x is in the
domain of f
and
y = f(x).
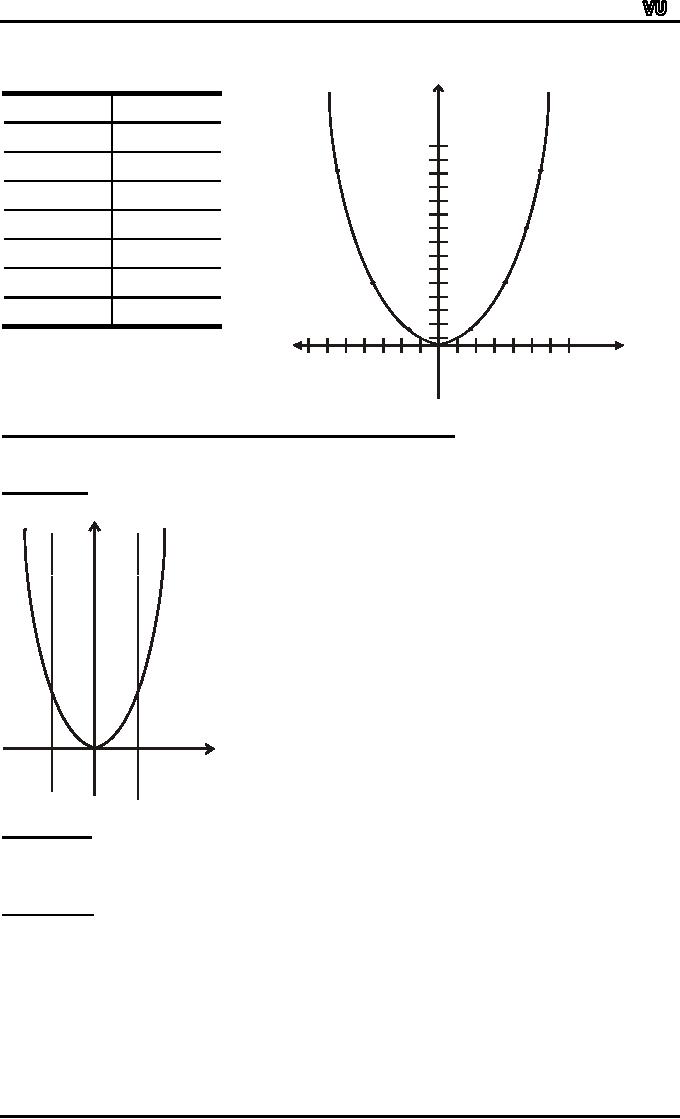
EXAMPLE:
We
have to draw the graph of
the function f given by the
relation y=x2 in
order to draw the
graph
of the function we will
first take some elements
from the domain will
see the image of
them
and then plot then on
the graph as follows
Graph
of y = x2
Page
60
MTH001
Elementary Mathematics
y
= x2
y
x
y=f(x)
-3
9
-2
4
(3,9)
(-3,9)
-1
1
0
0
(x
, f(x))
+1
1
(2,4)
(-2,4)
+2
4
+3
9
(1,1)
(-1,1)
O
(o,o)
x
VERTICAL
LINE TEST FOR THE
GRAPH OF A FUNCTION:
For
a graph to be the graph of a
function, any given vertical
line in its domain
intersects the
graph
in at most one point.
EXAMPLE:
The
graph of the relation y =
x2 on
R defines a function by vertical
line test.
y
y=x2
x
O
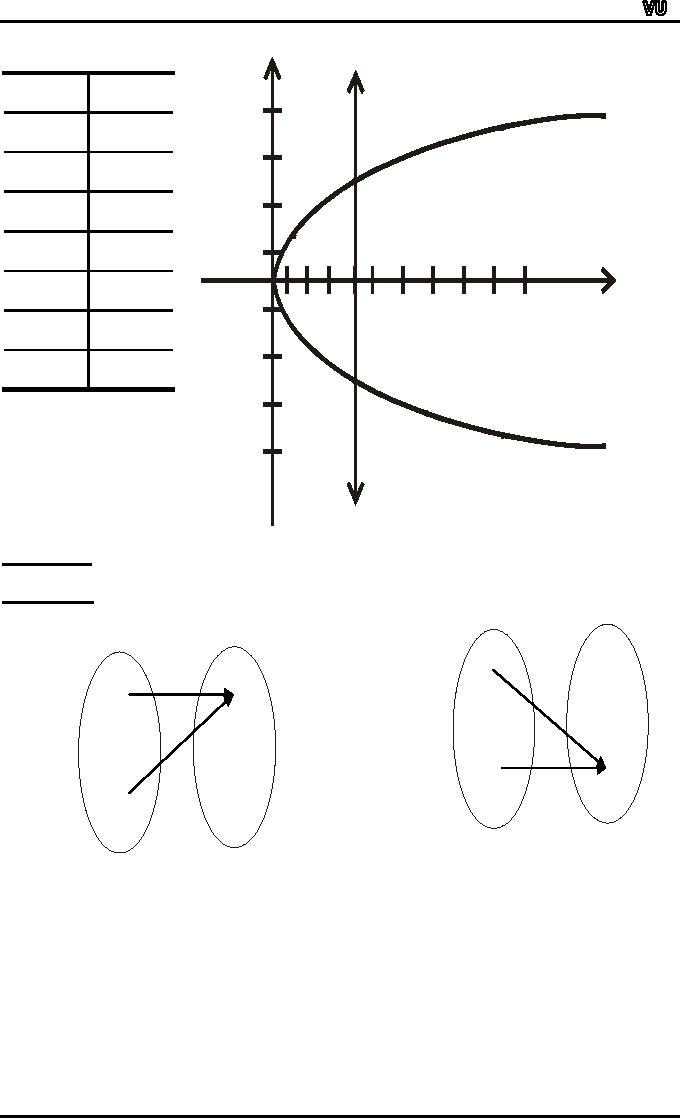
EXERCISE:
Define
a binary relation P from R to R as
follows:
for
all real numbers x and y
(x, y) ∈
P ⇔ x = y2
Is
P a function? Explain.
SOLUTION:
The
graph of the relation x =
y2 is
shown below. Since a
vertical line intersects the
graph at
two
points; the graph does
not define a
function.
Page
61
MTH001
Elementary Mathematics
x
Y
4
9
-3
(4,2)
3
4
-2
2
1
-1
0
0
1
0
-1
1
1
1
2 3 4 5 6 7 8 9 10
x
4
2
-2
9
3
(4,-2)
-3
-4
EXERCISE:
Find
all functions from X = {a,b}
to Y = {u,v}
SOLUTION:
1.
2.
a
u
a
u
Y
b
v
X
b
v
Page
62
MTH001
Elementary Mathematics
3.
4.
u
a
u
a
v
b
v
b
X
Y
X
Y
EXERCISE:
Find
four binary relations from X
= {a,b}to Y = {u,v}that are
not functions.
SOLUTION:
The
four relations are
1.
2.
.u
a.
a.
.u
b.
b.
.v
.v
X
Y
X
Y
X
Y
Y
3.
X
4.
a.
u.
a.
u.
b.
v.
b.
v.
EXERCISE:
How
many functions are there
from a set with three
elements to a set with four
elements.
SOLUTION:
Let
X = {x1,
x2, x3}
and Y= {y1,
y2, y3,y4}
Page
63
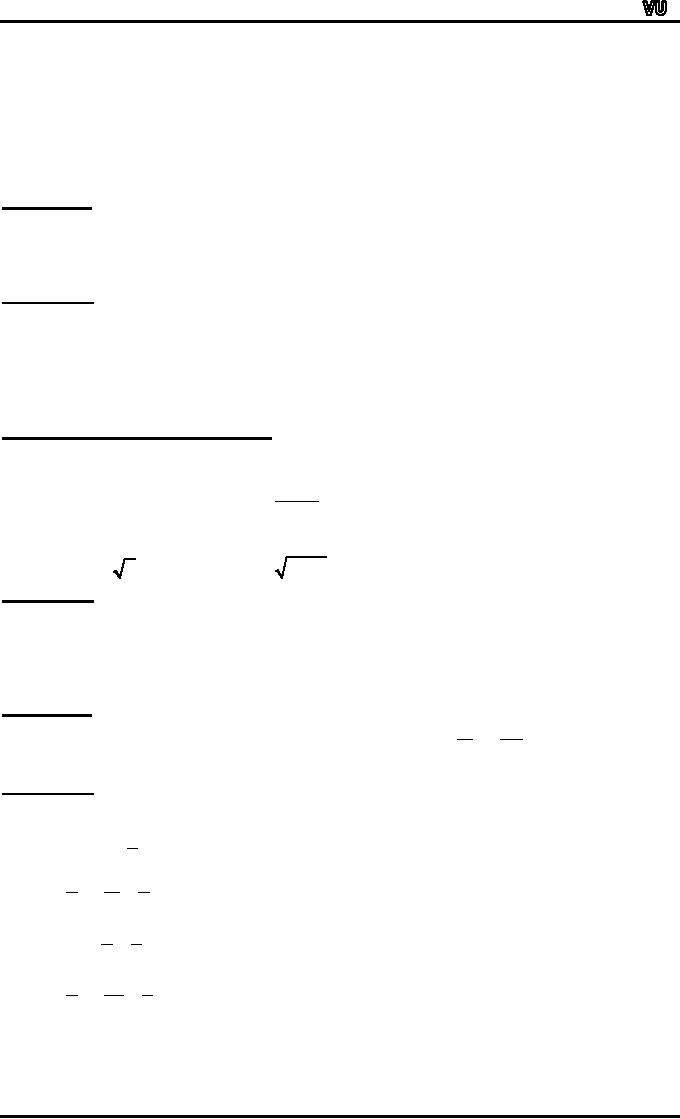
MTH001
Elementary Mathematics
Then
x1 may
be related to any of the
four elements y1, y2,
y3, y4
of Y. Hence
there are 4
ways
to relate x1 in
Y. Similarly x2
may
also be related to any one
of the 4 elements in Y.
Thus
the total number of
different ways to relate
x1 and
x2 to elements of Y are 4
× 4 =
16.
Finally
x3 must
also has its image in Y
and again any one of
the 4 elements y1, or
y2 or y3
or
y4 could be its
image.
Therefore
the total number of
functions from X to Y
are
4
×
4 × 4 = 43 =
64.
EXERCISE:
Suppose
A is a set with m elements
and B is a set with n
elements.
1.How
many binary relations are
there from A to B?
2.How
many functions are there
from A to B?
3.What
fraction of the binary
relations from A to B are
functions?
SOLUTION:
1.Number
of elements in A ×
B =
m.n
Therefore,
number of binary relations
from A to B =
Number
of all subsets of A ×
B =
2mn
2.Number
of functions from A to B = n.n.n. ... .n
(m
times)
m
=n
3.Fraction
of binary relations that are
functions = n m /
2mn
FUNCTIONS
NOT WELL DEFINED:
Determine
whether f is a function from Z to R
if
1
f
(n)
=
±n
f
(n)
=
a.
b.
n2 -
4
f
(n)
=
n
f
(n)
=
n2 +
1
c.
d.
SOLUTION:
a.
f
is not well defined since
each integer n has two
images +n and -n
b.
f
is not well defined since
f(2) and f(-2) are
not defined.
c.
f
is not defined for n < 0
since f then results in
imaginary values (not
real)
d.
f
is well defined because each
integer has unique (one
and only one) image in
R
under
f.
EXERCISE:
2
⎛m⎞
m
Student
C tries to define a function h : Q
→
Q by
the rule.
h⎜
⎟ =
for
all integers m and n with n
≠
0
⎝n⎠
n
Students
D claims that h is not well
defined. Justify students
D's claim.
SOLUTION:
The
function h is well defined if
each rational number has a
unique (one and only
one)
image.
1
∈Q
Consider
2
2
⎛1⎞
1
1
h⎜
⎟ = =
⎝
2⎠
2
2
12
=
Now
and
24
2
⎛
2⎞
2
4
h⎜
⎟ =
=
=1
⎝
4⎠
4
4
Hence
an element of Q has more
than one images under h.
Accordingly h is not
well
defined.
Page
64
MTH001
Elementary Mathematics
REMARK:
A
function f: X →
Y is
well defined iff
∀ x1,
x2 ∈X, if x1 =
x2 then f(x1) =
f(x2)
EXERCISE:
Let
g: R→R+
be defined by g(x) = x2 +1
1.
Show
that g is well
defined.
2.
Determine
the domain, co-domain and
range of g.
SOLUTION:
1.
g
is well defined:
Let
x1,
x2 ∈R and
suppose x1 = x2
x12 =
x22
⇒
(squaring
both sides)
2
2
⇒
x1 + 1 =
x2 + 1
(adding
1 on both sides)
⇒
g
(x1)
= g(x2)
(by definition of g)
Thus
if x1 =
x2 then g (x1) = g(x2).
According g:R →
R+ is
well defined.
g:R
→R+ defined
by g(x) = x2 +
1.
2.
Domain
of g = R (set of real
numbers)
Co-domain
of g = R+ (set of positive real
numbers)
The
range of g consists of those
elements of R+ that appear as image
points.
Since
x2 ≥0
∀
x ∈R
2
x
+ 1≥
1
∀
x ∈R
2
g(x)
= x + 1≥ 1
∀
x ∈R
i.e.
Hence
the range of g is all real
number greater than or equal
to 1, i.e., the internal
[1,∝)
IMAGE
OF A SET:
Let
f : X →Y
is function and A ⊆
X.
The
image of A under f is denoted
and defined as:
f(A)
= {y∈Y
| y=f(x), for some x in
A}
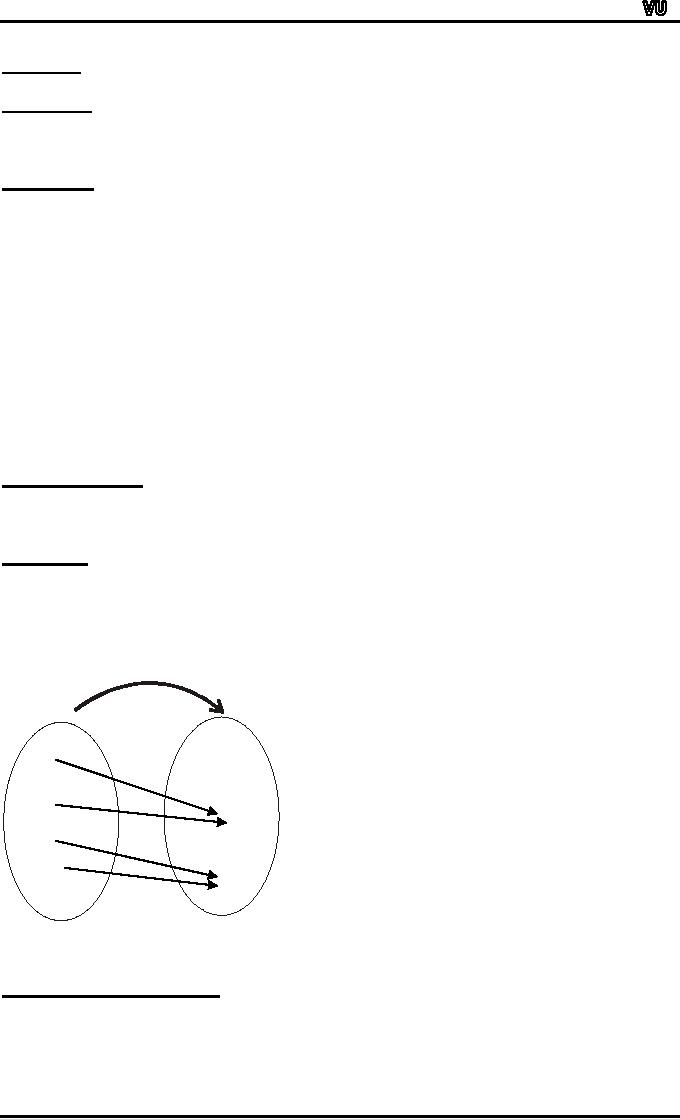
EXAMPLE:
Let
f: X →Y
be defined by the arrow
diagram
Let
A = {1,2}and B = {2,3}
then
f(A)={b}
and f(B) = {b,c} under
the function defined in the
Diagram then we say that
image
set
of A is {b} and I mage set
of B is {b,c}.
f
.a
1
2
b
3
4
c
X
Y
INVERSE
IMAGE OF A SET:
Let
f: X →Y
is a function and C ⊆
Y.
The inverse image of C under
f is denoted and
defined
as:
f-1(C)={x ∈X | f(x)
∈C}
Page
65
MTH001
Elementary Mathematics
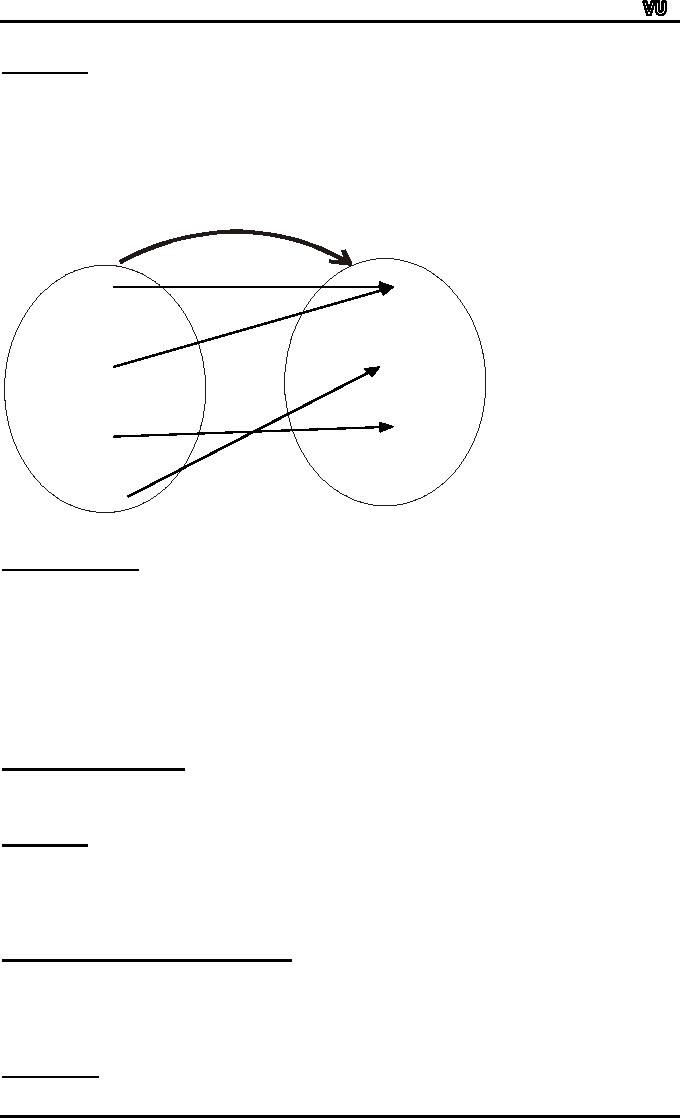
EXAMPLE:
Let
f: X →Y
be defined by the arrow
diagram.
Let
C = {a},D = {b,c},E = {d}
then
f-1(C)={1,2},
f-1(D) = {3,4},
and
f-1(E) =∅
f
X
Y
a
1
b
2
c
3
d
4
SOME
RESULTS:
Let
f: X →Y
is a function. Let A and B be
subsets of X and C and D be
subsets of Y.
if
A⊆
B
then f(A) ⊆
f(B)
1.
f(A∪B)
= f(A) ∪f(B)
2.
f(A∩B)
⊆
f(A)
∩
f(B)
3.
f(A-B)
⊃
f(A) -
f(B)
4.
if
C ⊆
D,
then f-1(C)
⊆ f-1(D)
5.
f-1(C∪D) = f-1(C) ∪
f-1((D)
6.
f-1(C∩D) = f-1(C) ∩f-1(D)
7.
f-1(C-D) = f-1
(C) -
f-1 (D)
8.
BINARY
OPERATIONS:
A
binary operation "*" defined
on a set A assigns to each
ordered pair (a,b) of
elements of A,
a
uniquely determined element
a*b of A.
That
is, a binary operation takes
two elements of A and maps
them to a third element of
A.
EXAMPLE:
1.
"+"
and "." are binary
operations on the set of
natural numbers N.
2.
"-"
is not a binary operation on
N.
3.
"-"
is a binary operation on Z, the
set of integers.
"÷"
is a binary operation on the
set of non-zero rational
numbers
4.
Q-{0},
but not a binary operation
on Z.
BINARY
OPERATION AS FUNCTION:
A
binary operation "*" on a
set A is a function from A * A to
A.
i.e.
*: A ×A
→A.
where
a, b, c ∈A.
Hence
*(a,b) = c,
NOTE
*(a,b)
is more commonly written as
a*b.
EXAMPLES:
Page
66
MTH001
Elementary Mathematics
1.The
set operations union ∪, intersection
∩
and
set difference -, are binary
operators on
the
power set P(A) of any
set A.
2.The
logical connectives ∨, ∧, →, ↔
are
binary operations on the set
{T, F}
3.
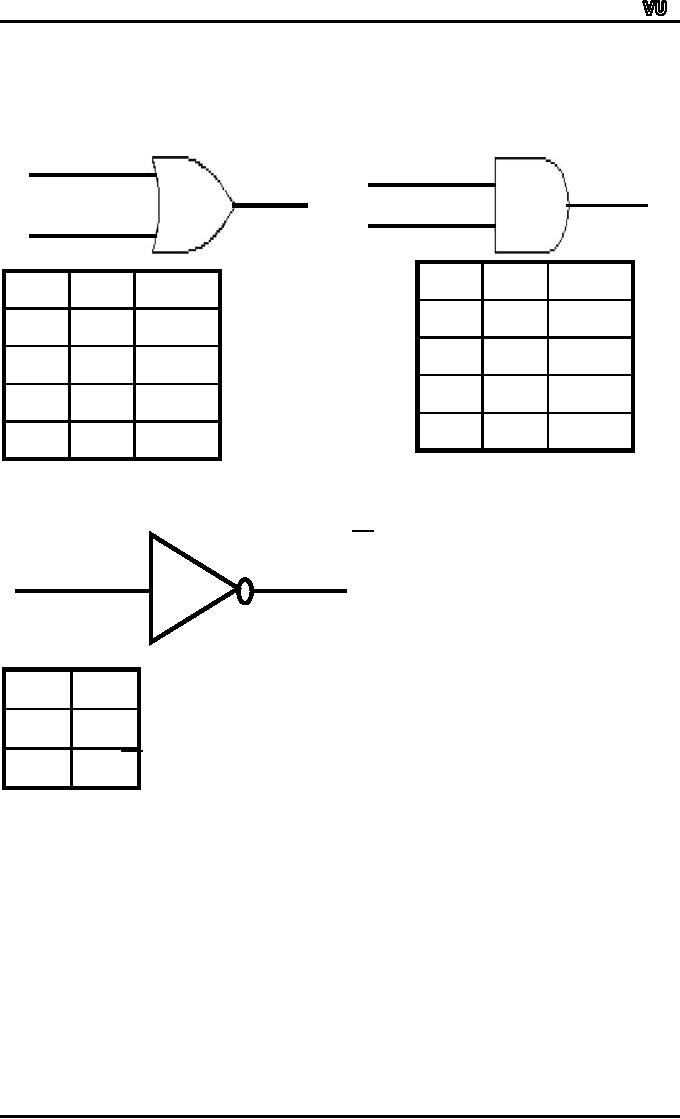
The
logic gates OR and AND are
binary operations on
{0,1}
A
A⋅B
A+B
A
OR
AND
B
B
A⋅B
A
B
A
B
A+B
1
1
1
1
1
1
1
0
0
1
0
1
0
1
0
0
1
1
0
0
0
0
0
0
4.
The
logic gate NOT is a uniary
operation on {0,1}
A
A
NOT
A
A
1
0
0
1
Page
67
Table of Contents:
- Recommended Books:Set of Integers, SYMBOLIC REPRESENTATION
- Truth Tables for:DE MORGAN’S LAWS, TAUTOLOGY
- APPLYING LAWS OF LOGIC:TRANSLATING ENGLISH SENTENCES TO SYMBOLS
- BICONDITIONAL:LOGICAL EQUIVALENCE INVOLVING BICONDITIONAL
- BICONDITIONAL:ARGUMENT, VALID AND INVALID ARGUMENT
- BICONDITIONAL:TABULAR FORM, SUBSET, EQUAL SETS
- BICONDITIONAL:UNION, VENN DIAGRAM FOR UNION
- ORDERED PAIR:BINARY RELATION, BINARY RELATION
- REFLEXIVE RELATION:SYMMETRIC RELATION, TRANSITIVE RELATION
- REFLEXIVE RELATION:IRREFLEXIVE RELATION, ANTISYMMETRIC RELATION
- RELATIONS AND FUNCTIONS:FUNCTIONS AND NONFUNCTIONS
- INJECTIVE FUNCTION or ONE-TO-ONE FUNCTION:FUNCTION NOT ONTO
- SEQUENCE:ARITHMETIC SEQUENCE, GEOMETRIC SEQUENCE:
- SERIES:SUMMATION NOTATION, COMPUTING SUMMATIONS:
- Applications of Basic Mathematics Part 1:BASIC ARITHMETIC OPERATIONS
- Applications of Basic Mathematics Part 4:PERCENTAGE CHANGE
- Applications of Basic Mathematics Part 5:DECREASE IN RATE
- Applications of Basic Mathematics:NOTATIONS, ACCUMULATED VALUE
- Matrix and its dimension Types of matrix:TYPICAL APPLICATIONS
- MATRICES:Matrix Representation, ADDITION AND SUBTRACTION OF MATRICES
- RATIO AND PROPORTION MERCHANDISING:Punch recipe, PROPORTION
- WHAT IS STATISTICS?:CHARACTERISTICS OF THE SCIENCE OF STATISTICS
- WHAT IS STATISTICS?:COMPONENT BAR CHAR, MULTIPLE BAR CHART
- WHAT IS STATISTICS?:DESIRABLE PROPERTIES OF THE MODE, THE ARITHMETIC MEAN
- Median in Case of a Frequency Distribution of a Continuous Variable
- GEOMETRIC MEAN:HARMONIC MEAN, MID-QUARTILE RANGE
- GEOMETRIC MEAN:Number of Pupils, QUARTILE DEVIATION:
- GEOMETRIC MEAN:MEAN DEVIATION FOR GROUPED DATA
- COUNTING RULES:RULE OF PERMUTATION, RULE OF COMBINATION
- Definitions of Probability:MUTUALLY EXCLUSIVE EVENTS, Venn Diagram
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:ADDITION LAW
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:INDEPENDENT EVENTS