REFLEXIVE RELATION:SYMMETRIC RELATION, TRANSITIVE RELATION

<< ORDERED PAIR:BINARY RELATION, BINARY RELATION

REFLEXIVE RELATION:IRREFLEXIVE RELATION, ANTISYMMETRIC RELATION >>

MTH001 Elementary Mathematics

LECTURE # 9

REFLEXIVE RELATION:

Let R be a relation on a set A. R is reflexive if, and only if, for all a ∈ A,

(a, a) ∈R. Or equivalently aRa.

That is, each element of A is related to itself.

REMARK

R is not reflexive iff there is an element "a" in A such that

(a, a) ∉R. That is, some element "a" of A is not

related to itself.

EXAMPLE:

Let A = {1, 2, 3, 4} and define relations R1,R2, R3, R4 on

as follows:

R1 = {(1, 1), (3, 3), (2, 2), (4, 4)}

R2 = {(1, 1), (1, 4), (2, 2), (3, 3), (4, 3)}

R3 = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 3), (4, 4)}

R4 = {(1, 3), (2, 2), (2, 4), (3, 1), (4, 4)}

Then,

R1 is reflexive, since (a, a) ∈R1 for all a ∈A.

R2 is not reflexive, because (4, 4) ∉R2.

R3 is reflexive, since (a, a) ∈R3 for all a ∈A.

R4 is not reflexive, because (1, 1) ∉R4, (3, 3) ∉R4

DIRECTED GRAPH OF A REFLEXIVE RELATION:

The directed graph of every reflexive relation includes an arrow from every point to

the point itself (i.e., a loop).

EXAMPLE :

Let A = {1, 2, 3, 4} and define relations R1, R2, R3, and

on A by

Page 42

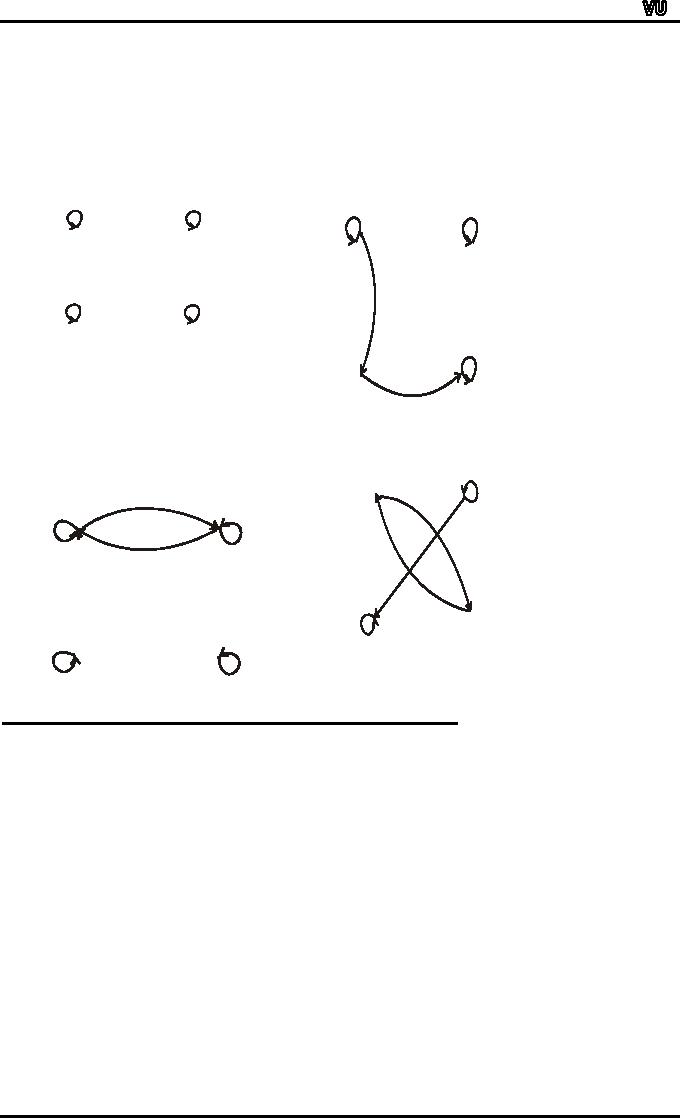
MTH001 Elementary Mathematics

R1 = {(1, 1), (3, 3), (2, 2), (4, 4)}

R2 = {(1, 1), (1, 4), (2, 2), (3, 3), (4, 3)}

R3 = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 3), (4, 4)}

R4 = {(1, 3), (2, 2), (2, 4),

(3, 1), (4, 4)}

Then their directed graphs are

R1 is reflexive because at

every point of the set A we

have a loop in the graph.

R2 is not reflexive, as there

is no loop at 4.

R4 is not reflexive, as there are

R3 is reflexive

no loops at 1and 3.

MATRIX REPRESENTATION OF A REFLEXIVE RELATION:

Let A = {a1, a2, ..., an}. A Relation R on A is reflexive if and only if

(ai, aj) ∈R ∀ i=1,2, ...,n.

Accordingly, R is reflexive if all the elements on the main diagonal of the

matrix M representing R are equal to 1.

EXAMPLE:

The relation R = {(1,1), (1,3), (2,2), (3,2), (3,3)} on A = {1,2,3}

represented by the following matrix M, is

reflexive.

1 2 3

1 ⎡1 0 1⎤

M = 2 ⎢0 1 0⎥

⎢

⎥

3 ⎢0 1 1⎥

⎣

⎦

SYMMETRIC RELATION

Let R be a relation on a set A. R is symmetric if, and only if,

for all a, b ∈ A, if (a, b) ∈R then (b, a) ∈R.

That is, if aRb then bRa.

Page 43

MTH001 Elementary Mathematics

REMARK

R is not symmetric iff there are elements a and b in A such that

(a,

b) ∈R but (b, a) ∉R.

EXAMPLE

Let A = {1, 2, 3, 4} and define relations R1, R2, R3, and R4on A as

follows.

R1 = {(1, 1), (1, 3), (2, 4), (3, 1), (4,2)}

R2 = {(1, 1), (2, 2), (3, 3), (4, 4)}

R3 = {(2, 2), (2, 3), (3, 4)}

R4 = {(1, 1), (2, 2), (3, 3), (4, 3), (4, 4)}

Then R1 is symmetric because for every order pair (a,b)in R1awe have (b,a) in

R1for example we have (1,3)in R1 the we have (3,1) in R1 similarly all other

ordered pairs can be cheacked.

R2 is also symmetric symmetric we say it is vacuously true.

R3 is not symmetric, because (2,3) ∈ R3 but (3,2) ∉ R3.

R4 is not symmetric because (4,3) ∈ R4 but (3,4) ∉ R4.

DIRECTED GRAPH OF A SYMMETRIC RELATION

For a symmetric directed graph whenever there is an arrow

going from one

point

of the graph to a second, there is an arrow going from the second point back to the

first.

EXAMPLE

Let A = {1, 2, 3, 4} and define relations R1, R2, R3, and R4 on

A by the directed graphs:

R1 = {(1, 1), (1, 3), (2, 4), (3, 1), (4,2)}

R2 = {(1, 1), (2, 2), (3, 3), (4, 4)}

R3 = {(2, 2), (2, 3), (3, 4)}

R4= {(1, 1), (2, 2), (3, 3), (4, 3), (4, 4)}

Page 44

Table of Contents: