Pumping Lemma

<< Nonregular languages

Pumping Lemma version II >>

Theory of Automata

(CS402)

Theory of Automata

Lecture N0. 26

Reading Material

Introduction to Computer Theory

Chapter 10

Summary

Example of nonregular language, pumping lemma version I, proof, examples

Example

Consider the language L = {Λ, ab, aabb, aaabbb, ...} i.e. {an bn : n=0,1,2,3,...}

Suppose, it is required to prove that this language is nonregular. Let, contrary, L be a regular language then by

Kleene's theorem it must be accepted by an FA, say, F. Since every FA has finite number of states then the

language L (being infinite) accepted by F must have words of length more than the number of states. Which

shows that, F must contain a circuit.

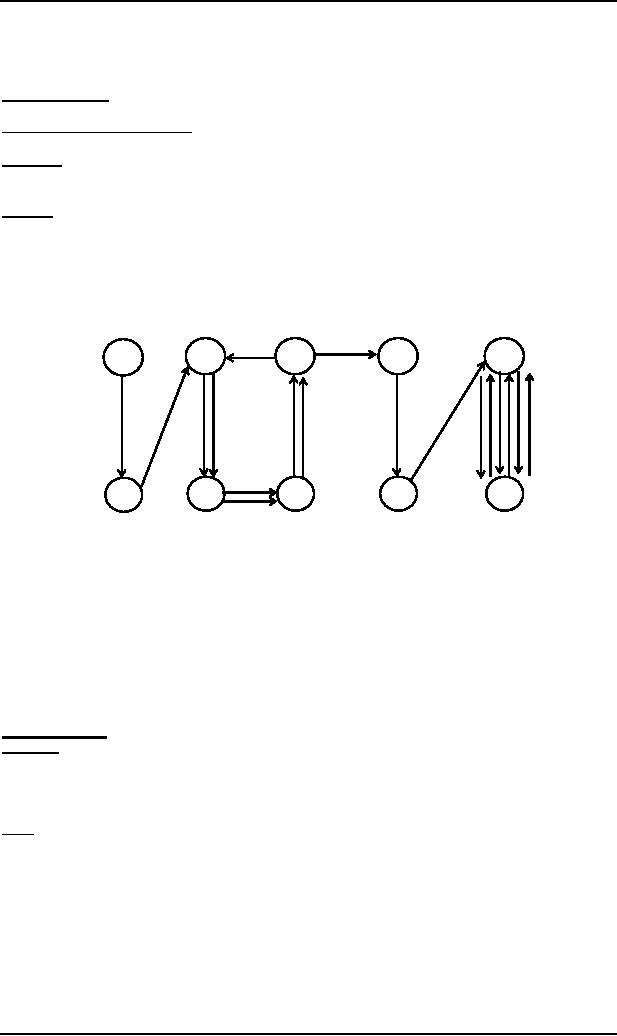
For the sake of convenience suppose that F has 10 states. Consider the word a9 b9 from the language L and let

the path traced by this word be shown as under

But, looping the circuit generated by the states 3,4,6,5,3 with a-edges once more, F also accepts the word a9+4 b9,

while a13b9 is not a word in L. It may also be observed that, because of the circuit discussed above, F also

accepts the words a9(a4 )m b9, m = 1,2,3, ...

Moreover, there is another circuit generated by the states 9,10,9. Including the possibility of looping this circuit,

F accepts the words a9(a4 )m b9(b2 )n where m,n=0,1,2,3,...(m and n not being 0 simultaneously).Which shows

that F accepts words that are not belonging to L.

Similarly for finding FAs accepting other words from L, they will also accept the words which do not belong to

Thus there is no FA which accepts the language L. which shows, by Kleene's theorem, that the language L can't

be expressed by any regular expression. It may be noted that apparently anbn seems to be a regular expression of

L, but in fact it is not. The observations made from this example, generalize the theorem (also called the

Pumping lemma) regarding the infinite regular language as follows

Pumping Lemma

Statement

Let L be any infinite regular language (that has infinite many words), defined over an alphabet Â then there exist

three strings x, y and z belonging to Â* (where y is not the null string) such that all the strings of the form xynz

for n=1,2,3, ... are the words in L.

Proof

If L is a regular language, then according to Kleene's theorem, there exists an FA, say, F that accepts this

language. Now F, by definition, must have finite no of states while the language has infinitely many words,

which shows that there is no restriction on the length of words in L, because if there were such restriction then

the language would have finite many words.

Let w be a word in the language L, so that the length of word is greater than the number of states in F. In this

case the path generated by the word w, is such that it cannot visit a new state for each letter i.e. there is a circuit

in this path.

The word w, in this case, may be divided into three parts

The substring which generates the path from initial state to the state which is revisited first while reading the

word w. This part can be called x and x can be a null string.

Theory of Automata

(CS402)

The substring which generates the circuit starting from the state which was lead by x. This part can be called as

y which cannot be null string.

The substring which is the remaining part of the word after y, call this part as z. It may be noted that this part

may be null string as the word may end after y or z part may itself be a circuit.

Thus the word may be written as w = xyz where x,y and z are the strings, also y can't be a null string.

Now this is obvious that, looping the circuit successively, the words xyyz, xyyyz, xyyyz, ... will also be

accepted by this FA i.e. xynz, n=1,2,3, ... will be words in L.

Remark: In the above theorem, it is not affected if the z-part has circuit. To prove the theorem it is only to find a

circuit and then looping that circuit, is all that is needed. While looping the circuit the volume of the string y

(or z) is pumped, so the theorem is also called the Pumping lemma. Following are the examples

Example

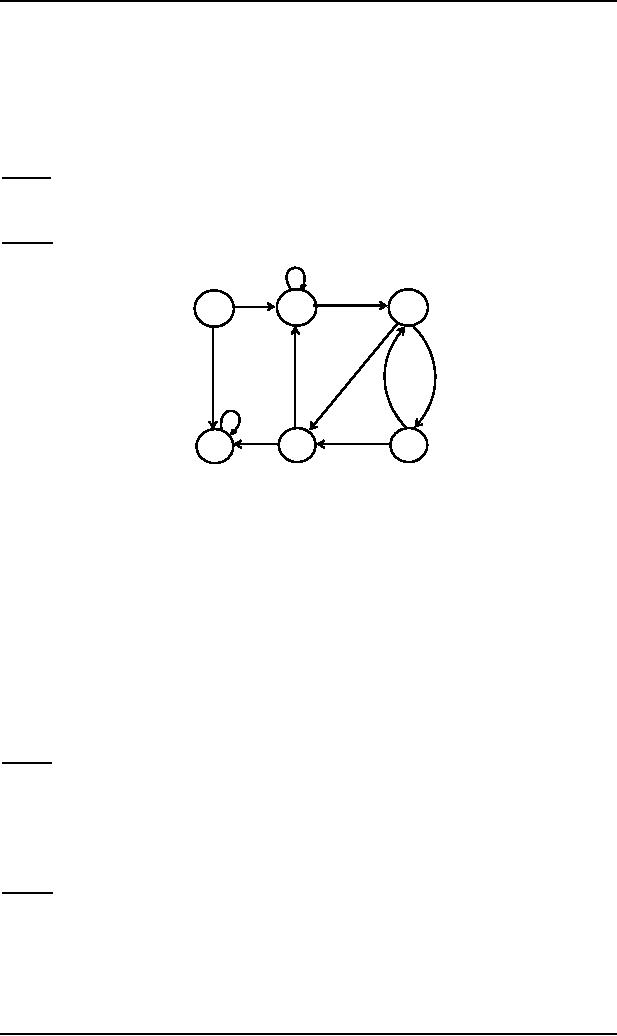
Consider the following 5 states FA, say, F which accepts an infinite language

a,b

Let the word w = bbbababa, belonging to the language L, so that the length of word is greater than 6 (the

number of states in F).

In this case the path generated by this word is such that it cannot visit a new state for each letter i.e. there is a

circuit in this path.

The word w, in this case, may be divided into three parts.

The substring which generates the path from initial state to the state which is revisited first while reading the

word w. This can be called as part x and this may be null string.

The substring which generates the circuit starting from the start state which was lead by x, this part can be called

as y and this cannot be null string.

The substring which is the remaining part of the word after y, this part can be called as z. It may be noted that

this part may be null string as the word may end after y or z-part may itself be a circuit.

Thus the word w may be written as w = xyz, where x,y,z are strings belonging to Â* and y cannot be null string.

The state 2 is such that it is revisited first while reading the word w. So the word w can be decomposed,

according to pumping lemma, as w = xyz = (b)(bba)(baba)

If y-part of w is continuously pumped, the resulting strings will be accepted by F and hence will be words in the

language accepted by F. Thus, by pumping lemma, the language accepted by F is regular.

Remark: If the pumping lemma is applied directly on the language L = {an bn : n=0,1,2,3,...}, it can be observed

that for the word w = (aaa)(aaaabbbb)(bbb)

where x = aaa, y = aaaabbbb and z = bbb

xyyz will contain as many number of a's as there are b's but this string will not belong to L because the

substring ab can occur at the most once in the words of L, while the string xyyz contains the substring ab twice.

On the other hand if y-part consisting of only a's or b's, then xyyz will contain number of a's different from

number of b's. This shows that pumping lemma does not hold and hence the language is not regular.

Example

Consider the language EQUAL, of strings, defined over Σ={a,b}, with number of a's equal to number of b's,

i.e. EQUAL = {Λ ,ab,aabb,abab,baba,abba,...}

From the definition of EQUAL, it is clear that {an bn } = a* b* Č EQUAL

Obviously a* b* defines a regular language while {an bn } has been proved nonregular.

Using the theorem that intersection of two regular languages is, regular; it can be proved that the EQUAL is not

regular. Because if it is considered regular then the language {an bn } will, being intersection of regular

languages, be regular language, which is impossible.

Theory of Automata

(CS402)

Following are the remarks regarding these examples

Remarks

In the previous examples, languages are proved to be regular or nonregular using pumping lemma. In fact to

prove a certain language to be regular, it is not needed to use the full force of pumping lemma i.e. for a word

with length greater than the number of states of the machine, decomposing the word into xyz and for a language

to be regular it is sufficient that xyyz is in L. The condition that xynz is in L for n>2, provides that the language

is infinite.

Consider the language PALINDROME and a word w = aba belonging to PALINDROME. Decomposing

w = xyz where x=a, y=b, z=a. It can be observed that the strings of the form xynz for n=1,2,3, ..., belong to

PALINDROME. Which shows that the pumping lemma holds for the language PALINDROME (which is non

regular language). To overcome this drawback of pumping lemma, a revised version of pumping lemma is to be

introduced.

Table of Contents: