 |
Introduction
to Computing CS101
VU
LESSON
8
BINARY
NUMBERS & LOGIC
OPERATIONS
The
focus of the last Lesson was
on the microprocessor
During
that Lesson we learnt about
the function of the central component of a computer,
the
microprocessor
And
its various
sub-systems
Bus
interface unit
Data &
instruction cache
memory
Instruction
decoder
ALU
Floating-point
unit
Control
unit
Learning
Goals for Today
To
become familiar with number
system used by the microprocessors -
binary numbers
To
become able to perform
decimal-to-binary conversions
To understand the
NOT, AND, OR and XOR logic
operations the fundamental operations that
are
available
in all microprocessors
BINARY
(BASE
2)
numbers
DECIMAL
(BASE
10)
numbers
Decimal
(base 10) number system
consists of 10 symbols or
digits
0 12 3 4
5 67 8 9
Binary
(base 2) number system
consists of just
two
01
Other
popular number
systems
Octal
base
= 8
8 symbols
(0,1,2,3,4,5,6,7)
Hexadecimal
base
= 16
16 symbols
(0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F)
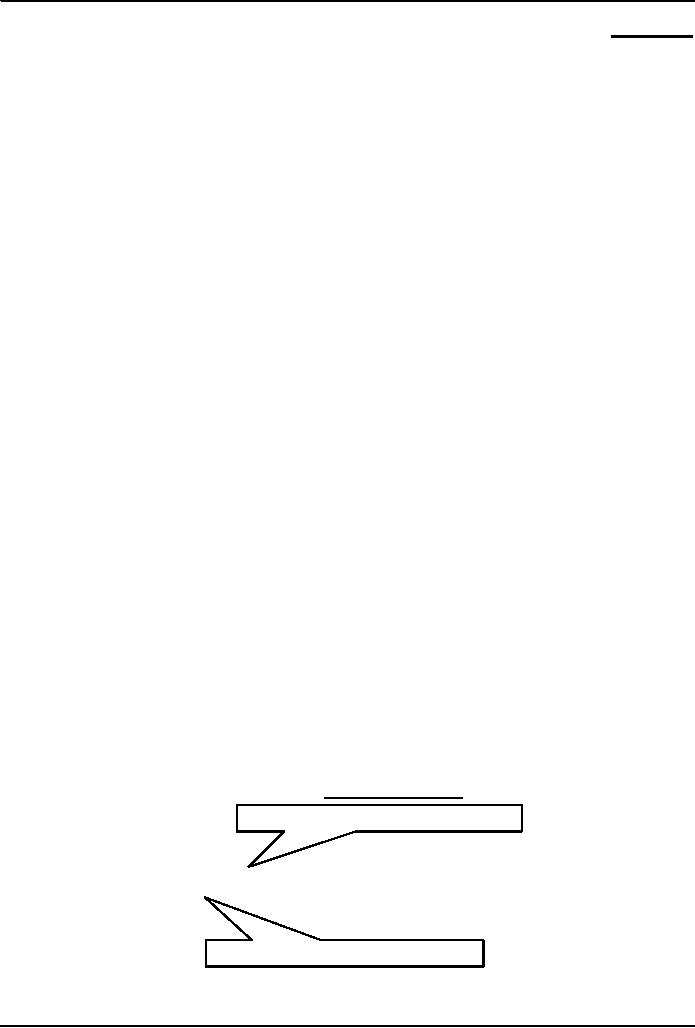
Decimal
(base 10) numbers are
expressed in the
positional
notation
The
right-most is the least
significant digit
4202 =
2x100 + 0x101 + 2x102 +
4x103
The
left-most is the most
significant digit
32
Introduction
to Computing CS101
VU
Decimal
(base 10) numbers are
expressed
in the
positional
notation
10
4202 =
2x100 + 0x101 + 2x102 +
4x103
10's
multiplier
Decimal
(base 10) numbers are
expressed
in the
positional
notation
1
4202 =
2x100 + 0x101 + 2x102 +
4x103
1's
multiplier
Decimal
(base 10) numbers are
expressed
in the
positional
notation
100
4202 =
2x100 + 0x101 + 2x102 +
4x103
100's
multiplier
33
Introduction
to Computing CS101
VU
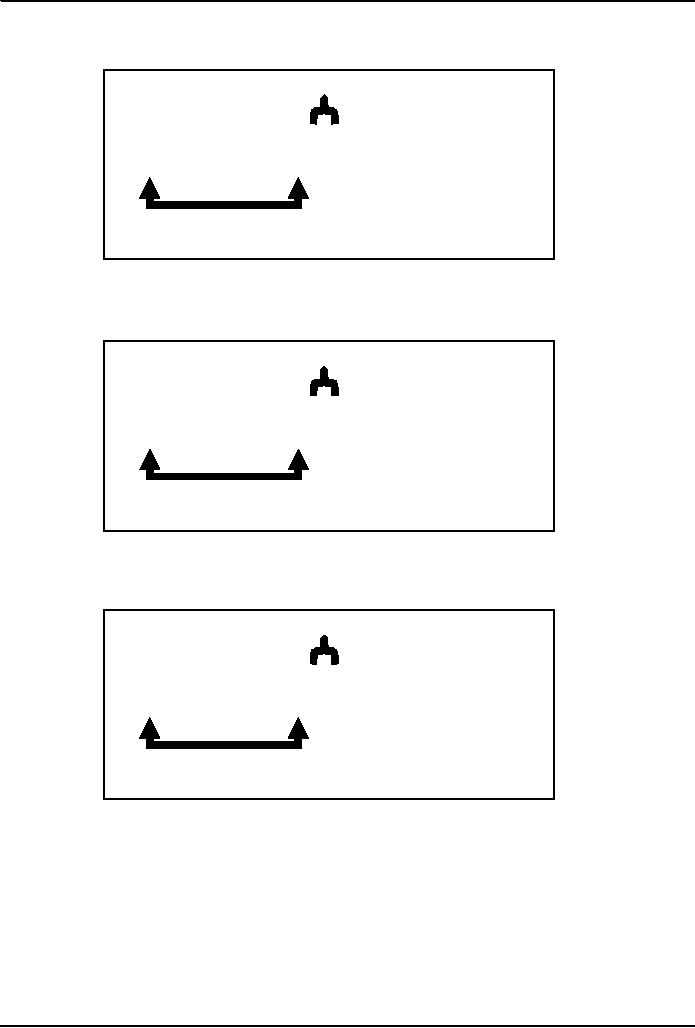
Binary
(base 2) numbers are also
expressed in
the
positional
notation
The
right-most is the least
significant
di i
10011 =
1x20 + 1x21 + 0x22 + 0x23 + 1x24
Binary
(base 2) numbers are also
expressed
in the
positional
notation
The
left-most is the most
significant digit
1
10011 =
1x20 + 1x21 + 0x22
+ 0x23 + 1x24
1's
multiplier
Binary
(base 2) numbers are also
expressed in
the
positional
notation
8
10011 =
1x20 + 1x21 + 0x22 + 0x23 + 1x24
8's
multiplier
Binary
(base 2) numbers are also
expressed in
the
positional
notation
16
10011 =
1x20 + 1x21 + 0x22 + 0x23 + 1x24
16's
multiplier
34
Introduction
to Computing CS101
VU
Counting
in
Counting
in
Decimal
Binary
10100
11110
20
30
0
1010
0
10
1
1011
10101
11111
11
21
31
1
10110
100000
32
10
1100
2
12
22
1101
10111
100001
23
33
11
3
13
100010
100
1110
11000
14
24
34
4
11001
100011
25
35
101
1111
5
15
10000
11010
100100
16
26
36
110
6
11011
.
.
111
10001
7
17
27
10010
11100
.
28
.
1000
8
18
10011
11101
.
29
1001
9
19
.
8.1
Why binary
Because
this system is natural for
digital computers
The
fundamental building block of a
digital computer the switch
possesses two natural
states, ON &
OFF.
It is
natural to represent those
states in a number system that
has only two symbols, 1 and 0,
i.e. the
binary
number system
In
some ways, the decimal number system is
natural to us humans.
Why?
bit
binary
digit
Byte = 8
bits
Decimal
Binary
conversion
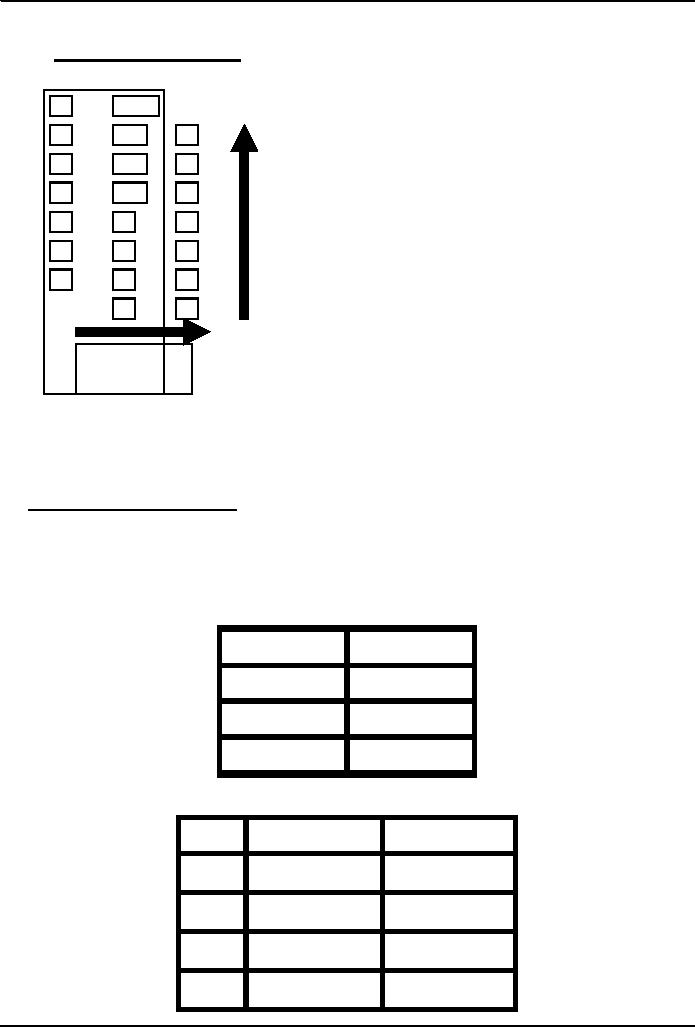
Convert 75 to
Binary
2
75
remainde
2
37
1
.
2
18
1
2
9
0
2
4
1
2
2
0
2
1
0
0
1
1001011
Check
1x20 + 1x21
+ 0x22 + 1x23
+ 0x24 + 0x25
+ 1x26
1001011
=
= 1 + 2
+ 0 + 8 + 0 + 0 + 64
=
75
35
Introduction
to Computing CS101
VU
Convert
100 to Binary
remainder
100
2
2
50
0
0
2
25
1
2
12
0
6
2
0
2
3
1
2
1
1
0
1100100
That
finishes our first topic -
introduction to binary numbers and
their conversion to and from
decimal
numbers
Our
next topic is ...
8.2
Boolean Logic Operations
Let
x,
y, z be
Boolean variables. Boolean
variables can only have
binary values i.e., they can
have
values
which are either 0 or
1.
For
example, if we represent the state of a
light switch with a Boolean
variable x, we
will assign a value
of 0 to
x
when
the switch is OFF, and 1 when it is
ON
A
few other names for
the states of these Boolean
variables
0
1
Off
On
Low
High
False
True
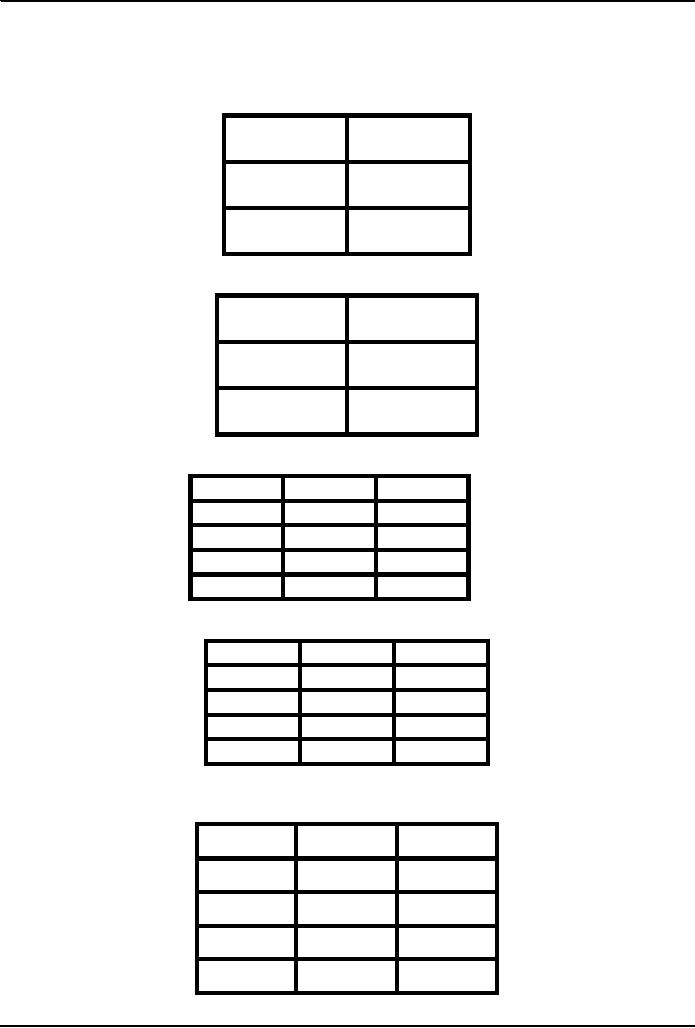
We
define the following logic
operations or functions among
the Boolean
variables
Name
Example
Symbolically
NOT
x´
y =
NOT(x)
AND
x·y
z = x
AND
y
OR
x+y
z = x
OR y
x⊕y
XOR
z = x
XOR
y
36
Introduction
to Computing CS101
VU
We'll
define these operations with the
help of truth tables
what
is the truth table of a logic
function
A
truth table defines the
output of a logic function
for all possible
inputs
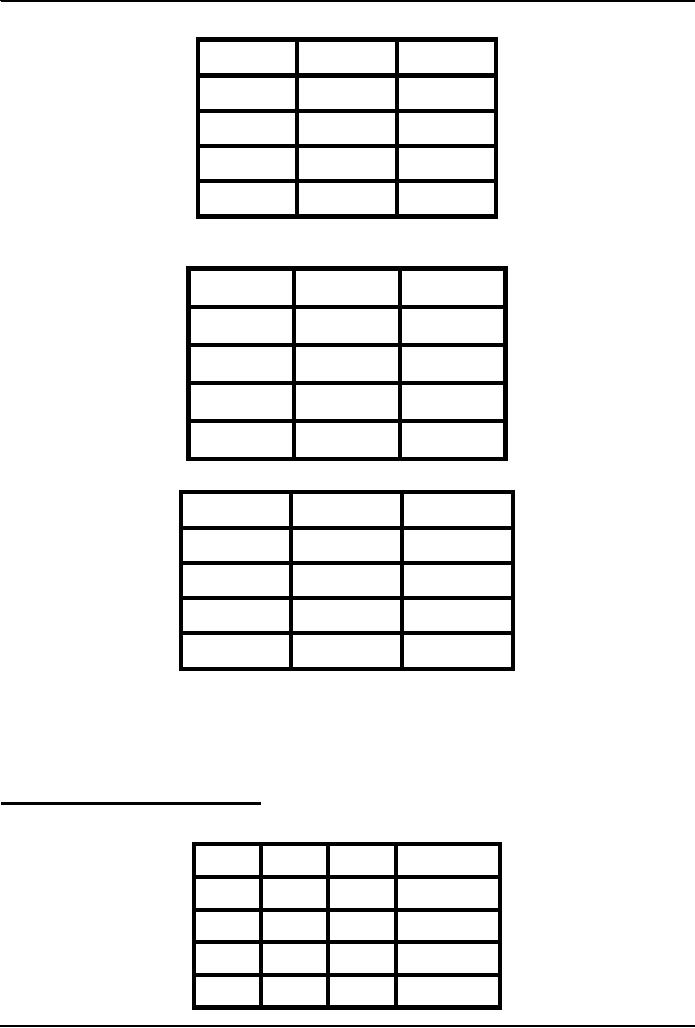
Truth
Table for the NOT
Operation
(y true
whenever x is false)
X
y =
x´
0
1
Truth
Table for the NOT
Operation
X
y =
x´
0
1
1
0
Truth
Table for the AND
Operation
(z
true when both x & y
true)
X
y
z=x·y
0
0
0
1
1
0
1
1
Truth
Table for the AND
Operation
X
y
z=x·y
0
0
0
0
1
0
1
0
0
1
1
1
Truth
Table for the OR
Operation
(z
true when x or y or both
true)
x
y
z=x+y
0
0
0
1
1
0
1
1
37
Introduction
to Computing CS101
VU
Truth
Table for the OR
Operation
x
y
z=x+y
0
0
0
0
1
1
1
0
1
1
1
1
Truth
Table for the XOR
Operation
(z
true when x or y true, but
not both)
z=x⊕y
X
y
0
0
0
1
1
0
1
1
8.3
Truth Table for the XOR
Operation
z=x⊕y
X
y
0
0
0
0
1
1
1
0
1
1
1
0
Those
4 were the fundamental logic
operations. Here are examples of a few
more complex
situations
z =
(x +
y)´
z = y
·
(x +
y)
z =
(y
·
x)
⊕
w
8.4
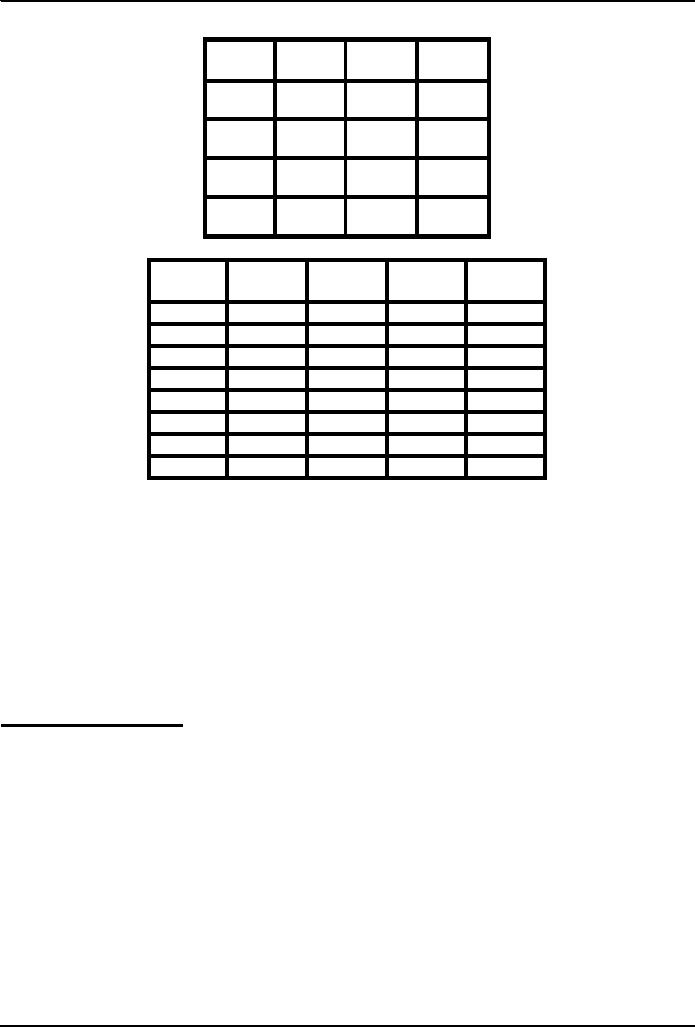
STRATEGY: Divide & Conquer
z =
(x +
y)´
z =
(x +
y)´
x
y
x+y
0
0
0
1
0
1
1
0
1
0
1
0
1
1
1
0
38
Introduction
to Computing CS101
VU
z = y
·
(x +
y)
z = y
·
(x
x
y
x+y
+
y)
0
0
0
0
0
1
1
1
1
0
1
0
1
1
1
1
z =
(y
·
x)
⊕
w
z =
(y
·
x)
x
y
W
y·x
⊕w
0
0
0
0
0
0
0
1
0
1
0
1
0
0
0
0
1
1
0
1
1
0
0
0
0
1
0
1
0
1
1
1
0
1
1
1
1
1
1
0
Number
of rows in a truth table?
2n
n =
number of input
variables
What
have we learnt
today?
About
the binary number system, and how it
differs from the decimal
system
Positional
notation for representing binary and
decimal numbers
A
process (or algorithm) which
can be used to convert
decimal numbers to binary
numbers
Basic
logic operations for Boolean
variables, i.e. NOT,
OR, AND, XOR, NOR,
NAND, XNOR
Construction
of truth tables (How many
rows?)
Focus
of the Next Lecture
Next
Lesson will be the 3rd on Web
dev
The
focus of the one after that, the
10th lecture, however,
will be on software. During
that Lesson we
will
try:
To understand the
role of software in
computing
To
become able to differentiate between
system and application
software
39
Table of Contents:
- INTRODUCTION
- EVOLUTION OF COMPUTING
- World Wide Web, Web’s structure, genesis, its evolution
- Types of Computers, Components, Parts of Computers
- List of Parts of Computers
- Develop your Personal Web Page: HTML
- Microprocessor, Bus interface unit, Data & instruction cache memory, ALU
- Number systems, binary numbers, NOT, AND, OR and XOR logic operations
- structure of HTML tags, types of lists in web development
- COMPUTER SOFTWARE: Operating Systems, Device Drivers, Trialware
- Operating System: functions, components, types of operating systems
- Forms on Web pages, Components of Forms, building interactive Forms
- APPLICATION SOFTWARE: Scientific, engineering, graphics, Business, Productivity, Entertainment, Educational Software
- WORD PROCESSING: Common functions of word processors, desktop publishing
- Interactivity to Forms, JavaScript, server-side scripts
- ALGORITHMS
- ALGORITHMS: Pseudo code, Flowcharts
- JavaScript and client-side scripting, objects in JavaScript
- Low, High-Level, interpreted, compiled, structured & object-oriented programming languages
- Software Design and Development Methodologies
- DATA TYPES & OPERATORS
- SPREADSHEETS
- FLOW CONTROL & LOOPS
- DESIGN HEURISTICS. Rule of thumb learned through trial & error
- WEB DESIGN FOR USABILITY
- ARRAYS
- COMPUTER NETWORKS: types of networks, networking topologies and protocols
- THE INTERNET
- Variables: Local and Global Variables
- Internet Services: FTP, Telnet, Web, eMail, Instant messaging, VoIP
- DEVELOPING PRESENTATIONS: Effective Multimedia Presentations
- Event Handlers
- GRAPHICS & ANIMATION
- INTELLIGENT SYSTEMS: techniques for designing Artificial Intelligent Systems
- Mathematical Functions in JavaScript
- DATA MANAGEMENT
- DATABASE SOFTWARE: Data Security, Data Integrity, Integrity, Accessibility, DBMS
- String Manipulations:
- CYBER CRIME
- Social Implications of Computing
- IMAGES & ANIMATION
- THE COMPUTING PROFESSION
- THE FUTURE OF COMPUTING
- PROGRAMMING METHODOLOGY
- REVIEW & WRAP-UP of Introduction to Computing