 |
Non-Context-Free language, Pumping lemma for CFLs |
| << Row language, Nonterminals |
| Decidablity, Parsing Techniques >> |
Theory of
Automata
(CS402)
Theory of
Automata
Lecture
N0. 43
Reading
Material
Introduction
to Computer Theory
Chapter
16
Summary
Non-Context-Free-languages,
Live Production, Dead Production, Theorem, self-
embedded nonterminal,
Pumping
lemma for CFLs,
Examples
Non-Context-Free
language
There
arises a question, whether all
languages are CFL? The
answer is no.
Languages
which are not Context-Free,
are called Non-CFL.
To prove
the claim that all
languages are not Context-Free, the
study of machines of word
production from the
grammar is
needed
Live
production: A production of the
form nonterminal ∆ string of
two nonterminals is called a live
production.
Dead
production: A production of the
form nonterminal ∆ terminal
is called a dead production.
It may be
noted that every CFG in
CNF has only these
types of productions.
Theorem
If a CFG
is in CNF and if there is restriction to
use the live production at
most once each, then
only the finite
many
words can be
generated.
It may be
noted that every time a live
production is applied during the
derivation of a word it increases
the
number of nonterminals
by one.
Similarly
applying dead production
decreases the nonterminals by one.
Which shows that to generate
a word,
one more
dead production are applied
than the live productions e.g.
S fi XY
fiaY
fiaa
Here one
live and two dead
productions are used.
In
general, if a CFG in CNF has
p live and q dead productions
then all words generated
without repeating any
live
production have at most
(p+1) letters.
Theorem
If a CFG
is in CNF with p live and q
dead productions and if w is word
generated by the CFG, having
more than
2p letters then any
derivation tree for w has a
nonterminal z which is used twice, where
the second z is the
descended
from the first z.
It can be
observed from the above
theorem that generation tree of
word w has more than p
rows.
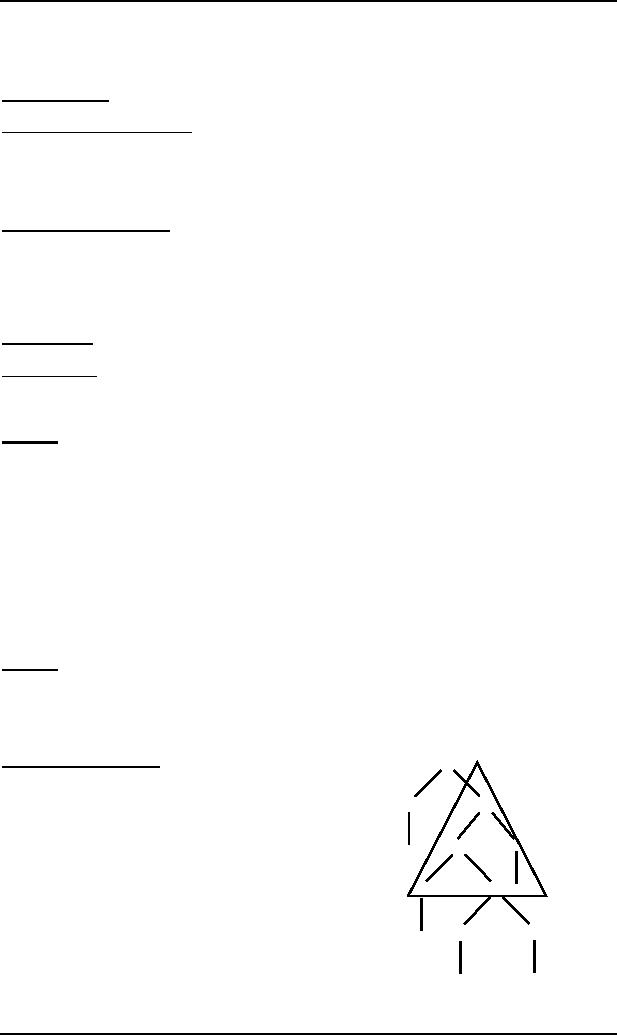
Self-embedded
nonterminal
S
A
nonterminal is said to be self-embedded,
if in a given derivation
of a
word, it ever occurs as a
tree
X
A
descendant
of itself, as shown in figure
aside
A
S
a
a
X
A
A
S
a
a
b
132
Theory of
Automata
(CS402)
Here the
nonterminal X is self-embedded.
Note
S
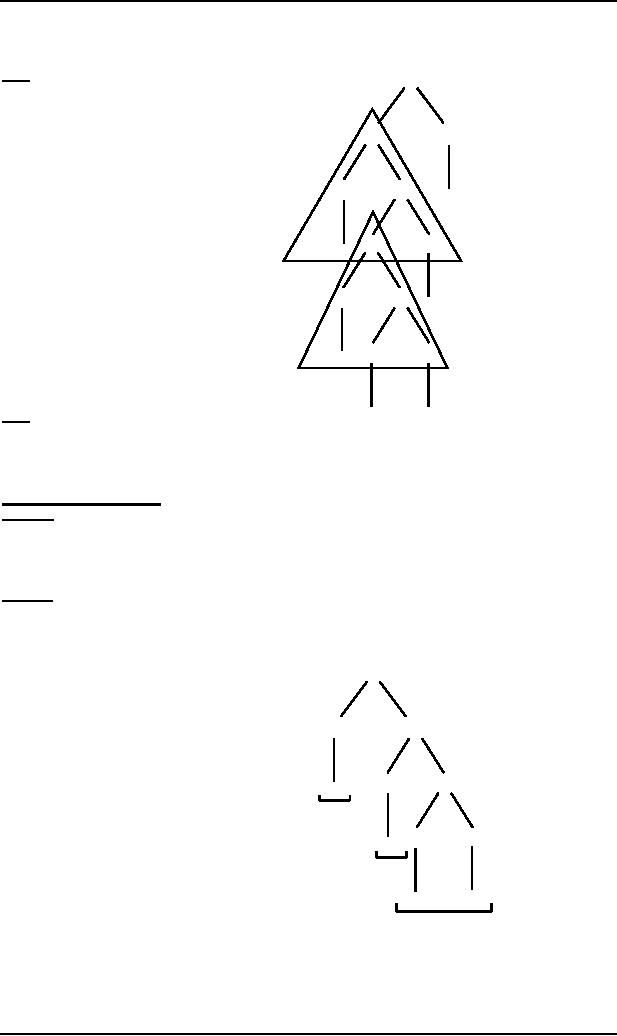
Consider
the following CFG in
CNF
S ∆ AB
A ∆ BC
B
A
C ∆ AB
A∆a
B∆b
C
B
and
the derivation tree of the
word bbabbb
b
A
B
b
C
B
b
A
B
b
a
b
Note
The part
of tree enclosed in upper triangle is
identical to that enclosed in lower
triangle, there is still
another
option of
replacing A by the same sequence of
production shown in lower
triangle.
The
above fact provides the
following pumping lemma for
the CFLs.
Pumping
lemma for CFLs
Theorem
If G is
any CFG in CNF with p
live productions, then every
word w of length more than 2p can be partitioned
into
five substrings as w = uvxyz,
where x is not null string and v
and y are not both null
string.
Then
all the words of the
form uvnxynz, n =
1,2,3,... can also be
generated by G.
Example
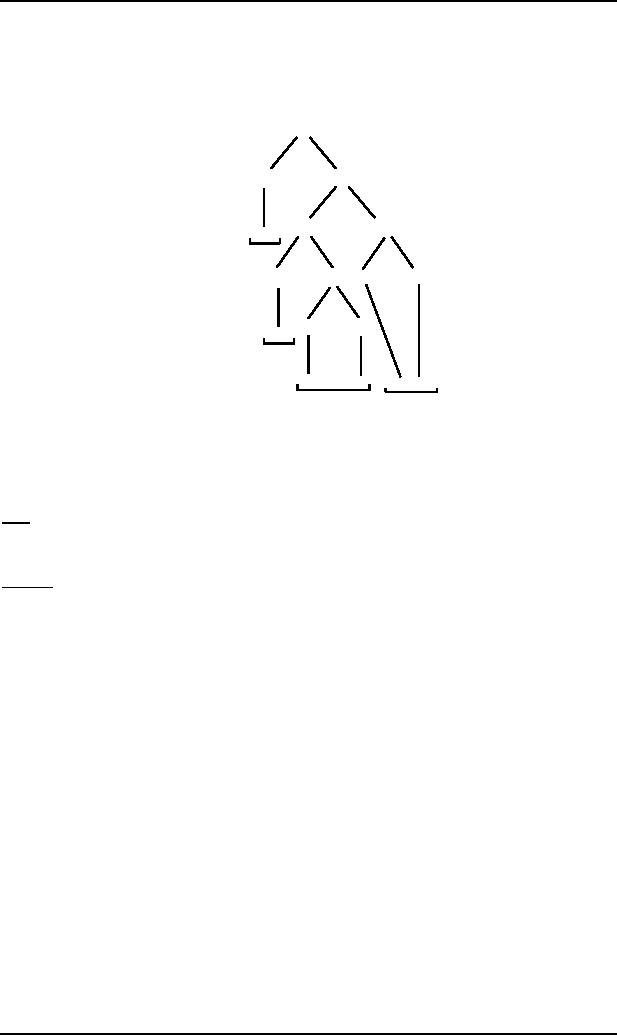
Consider
the following CFG which is
in CNF
S ∆ PQ
Q ∆ QS|b
P∆a
S
and a
word abab generated by the
above CFG with
the
following
derivation tree
Q
P
S
Q
a
u
Q
P
b
x
a
b
y
133
Theory of
Automata
(CS402)
Then w
can be broken up as w = uvxyz where u = a, v =
L, x = b, y =
ab, z = L
Repeating
the triangle from the
second Q just as it descends
from the first Q, the
corresponding tree may be
expressed
as follows
S
S
P
S
Q
a
u
S
Q
Q
P
Q
P
b
x
a
b
ab
y
y
Which
shows that uvvxyyz=aLLbababL=ababab
belongs to the language
generated by the given
CFG.
So, it
can be generalized that
words of the form uvnxynz, n=1,2,3,...
belong to the language
generated by the
given
CFG.
Note
It may be
noted that the pumping
lemma is satisfied by all CFLs
and the languages which
don't hold this
pumping
lemma, can't be Context Free
languages. Such languages
are non-CFLs.
Example
Consider
the language
L={anbncn :n=1,2,3,...}, let the
language L be Context Free language
and let the word
w=a200b200c200
of length
more than
2p, where p is the number of
live productions of its CFG in
CNF.
Note
It can be
observed that no matter what
choices are made for
the substrings u,v,x,y and
z, uv2xy2z
can't belong to
L, as all
the words in anbncn have
Only
one substring ab
Only
one substring bc
No
substring ac
No
substring ba
No
substring ca
No
substring cb
For
any n=1,2,3,...
The
above observations shows that if v or y
is not single letter or L, then
uv2xy2z
may contain either two or
more
substrings ab or bc or one or more
substrings ac or ba or ca or cb i.e.
these
strings may be in the
number
more than
the number they are supposed
to be.
Moreover,
if v and y are either single letter or L, then
one or two of letters a,b,c
will be increased, where as
the
other letter
will not be increased in uv2xy2z, which shows
uv2xy2z
does not belong to L.
Thus
pumping lemma is not satisfied.
Hence L is non CFL.
It may be
noted that the pumping
lemma discussed for infinite
regular language L, the
word w can be
decomposed
into three parts w=xyz, such
that all words of the
form xynz,
n=1,2,3,..., belong to L.
Similarly,
the pumping lemma discussed
for CFLs can also stated
as
134

Theory of
Automata
(CS402)
If w is a
large enough word in a CF:
then, w can be decomposed into w=uvxyz
such that all words of
the
form
uvnxynz
belong to L
It may be
noted that proof of pumping
lemma for regular languages
needed that path of word w
to be so large
enough so
that it contains a circuit
and circuit can be looped as
many times as one can.
The proof of the
pumping
lemma for CFLs needs
the derivation for w to be so large
that it contains a sequence of
productions
that
can be repeated as many
times as one can.
Moreover,
the pumping lemma for
regular languages does not
hold for non regular
language as that
language
does not
contain both xyz and
xyyz.
Similarly
pumping lemma for CFLs does
not hold for non-CFL as that
language does not contain both
uvxyz
and
uvvxyyz.
There is
another difference between
the pumping lemma for
regular languages and that
for CFLs that first
one
acts on
machines while other acts on algebraic
structures i.e.
grammar.
To achieve
full power the pumping
lemma for regular languages
has modified by pumping
lemma version II.
Similarly,
full power for pumping
lemma for CFLs is achieved by
stating the following
theorem
Theorem
If L is a
CFL in CNF with p live
productions then any word W in L of
length more than 2p
can be
decomposed
as
w=uvxyz s.t.
length(vxy)
≤
2p, length(x) > 0, length(v)+length(y)
> 0
then
the words of the form
uvnxynz :
n=1,2,3,... belong to L.
Example
Consider
the language
L= {anbmanbm :m,n=1,2,3,...}
={abab,aabaab,
abbabb, aabbaabb, aaabaaab,...
}
The
first version of pumping
lemma for CFLs may be
satisfied by L, but to apply the
second version of
pumping
lemma to
L, let L be generated by CFG which is in
CNF and has p live
productions.
Consider
the word decomposing w into
uvxyz where length(vxy) < 2p which shows that v
and y can't be single
letters
separated by clumps of other letter
because the separator letter is
longer than the length of
whole
substring
vxy, which shows that
uvvxyyz is not contained in L. Thus
pumping lemma is not satisfied
and L is
non
CFL.
135
Theory of
Automata
(CS402)
Example
Consider
the language EVENA i.e.
EVENA=(aa)n =a2n ={aa, aaaa,
aaaaaa, ...}
The
grammar for this language
must be
S ∆ SS|aa
and its CNF will
be
S ∆ SS|AA, A
∆
a,
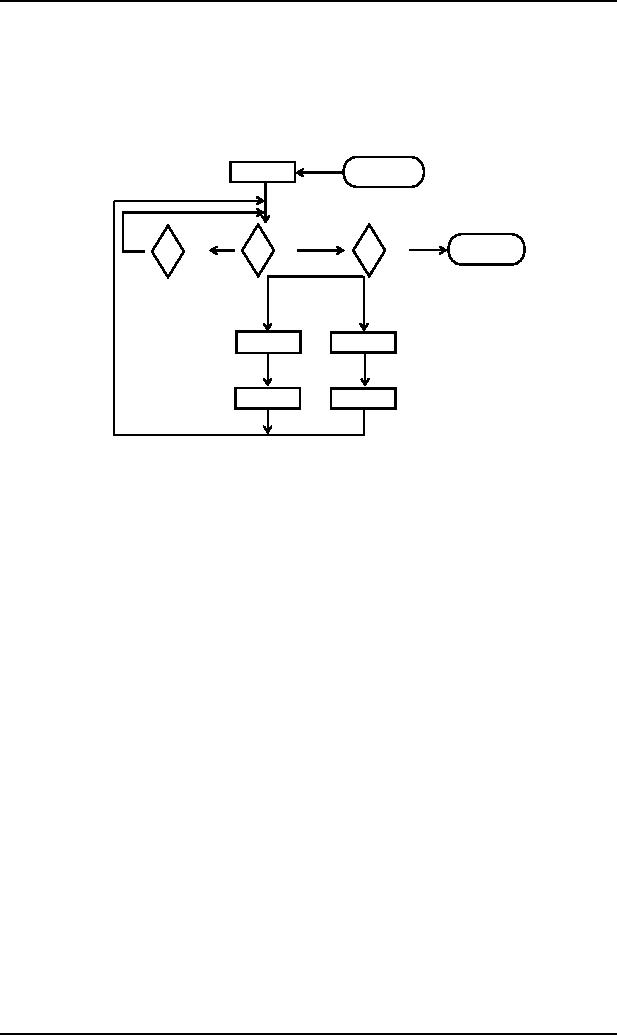
the PDA for this grammar
will be as under
PUSH
S
START
A
a
D
D
READ2
READ1
POP
ACCEPT
S
S
PUSH
A
PUSH
S
PUSH
A
PUSH
S
Its corresponding
conversion
form will
be
136
Theory of
Automata
(CS402)
$
START
PUSH
$
POP
A
$
PUSH
S
POP
POP
POP
S
a
a
a
PUSH
S
READ1
A
PUSH
A
POP
PUSH
$
$
HERE
POP
PUSH
$
POP
POP
READ2
S
S
D
PUSH
A
PUSH
S
POP
PUSH
S
PUSH
A
$
ACCEPT
The
summary table corresponding to the
above PDA in conversion
form can be
expressed as
FROM
TO
READ
POP
PUSH
ROW
START
L
HERE
$
S$
1
L
HERE
HERE
S
SS
2
L
HERE
HERE
S
AA
3
L
HERE
READ1
A
--
4
READ1
HERE
a
S
S
5
RAED1
HERE
a
$
$
6
READ1
HERE
a
A
A
7
L
HERE
READ2
$
$
8
READ2
D
ACCEPT
$
--
9
137

Theory of
Automata
(CS402)
Following
are the productions defined
from the summary
table
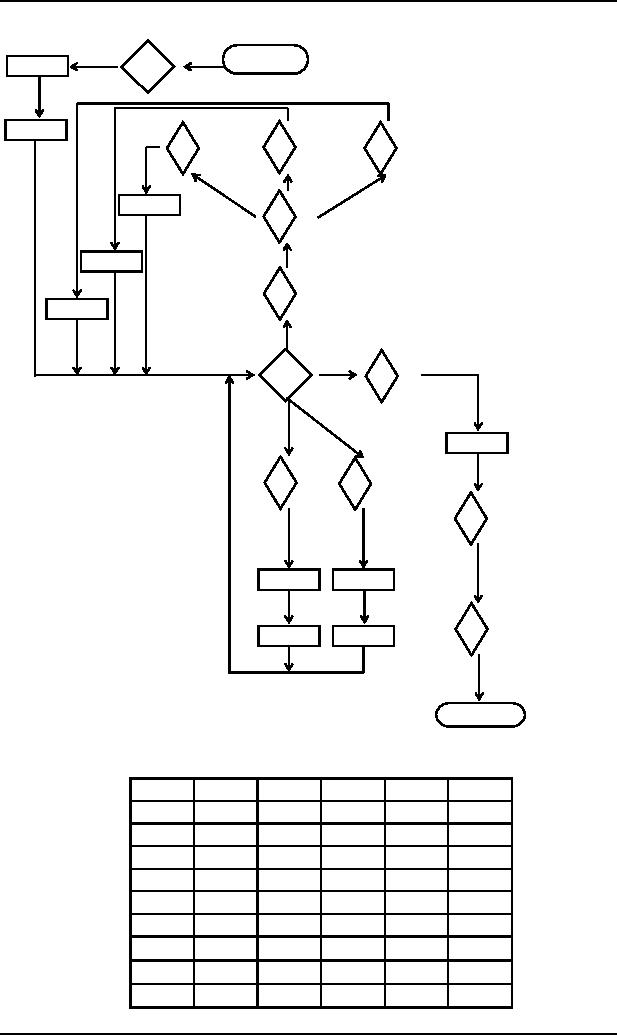
S ∆ Net(START,
ACCEPT, $)
Net(HERE,
READ1, A) ∆ Row4
Net(READ2, ACCEPT, $) ∆ Row9
Net(START,
X, $) ∆
Row1 Net(HERE, Y, S)Net(Y, X,
$)
Net(HERE,
X, S) ∆
Row2 Net(HERE, Y, S)Net(Y, X,
S)
Net(START,
X, S) ∆
Row3 Net(HERE, Y, A)Net(Y, X,
A)
Net(READ1, X, S) ∆ Row5 Net(HERE, X, S) gives four
productions
Net(READ1, X, $) ∆ Row6 Net(HERE, X, $) gives four
productions
Net(READ1, X, A) ∆ Row7 Net(HERE, X, A) gives four
productions
Net(HERE,
ACCEPT, $) ∆ Row8 Net(READ2,
ACCEPT, $)
Where X
and Y are the corresponding
joints
In
addition to 44 productions following 9 productions
complete the required
CFG
Row1 ∆
L
Row2 ∆
L
Row3 ∆
L
Row4 ∆
L
Row5 ∆ a
Row6 ∆ a
Row7 ∆ a
Row8 ∆
L
Row9 ∆
L
138
Table of Contents:
- What does automata mean, Introduction to languages
- Kleene Star Closure, Recursive definition of languages
- Regular Expression, Recursive definition of Regular Expression
- Equivalent Regular Expressions
- Finite Automaton
- Equivalent FAs
- FA corresponding to finite languages
- Examples of TGs: accepting all strings
- Generalized Transition Graphs
- Nondeterminism, Kleeneís Theorem
- Proof(Kleeneís Theorem Part II)
- Kleeneís Theorem Part III
- Concatenation of FAs
- Closure of an FA
- Nondeterministic Finite Automaton, Converting an FA to an equivalent NFA
- NFA with Null String
- NFA and Kleeneís Theorem
- NFA corresponding to Concatenation of FAs
- Distinguishable strings and Indistinguishable strings
- Finite Automaton with output, Moore machine
- Mealy machine
- Equivalent machines
- Mealy machines in terms of sequential circuit
- Regular languages, Complement of a language
- Nonregular languages
- Pumping Lemma
- Pumping Lemma version II
- Pseudo theorem
- Decidability
- finiteness of a language
- Context Free Grammar (CFG), CFG terminologies
- Trees
- Polish Notation (o-o-o)
- Total language tree, Regular Grammar
- Null Production
- Chomsky Normal Form (CNF)
- A new format for FAs
- Nondeterministic PDA
- PDA corresponding to CFG
- Conversion form of PDA
- Conversion Form, Joints of the machine
- Row language, Nonterminals
- Non-Context-Free language, Pumping lemma for CFLs
- Decidablity, Parsing Techniques
- Turing machine