 |
Mealy machines in terms of sequential circuit |
| << Equivalent machines |
| Regular languages, Complement of a language >> |
Theory of
Automata
(CS402)
Theory of
Automata
Lecture
N0. 23
Reading
Material
Introduction
to Computer Theory
Chapter
8
Summary
Mealy
machines in terms of sequential
circuit
Example
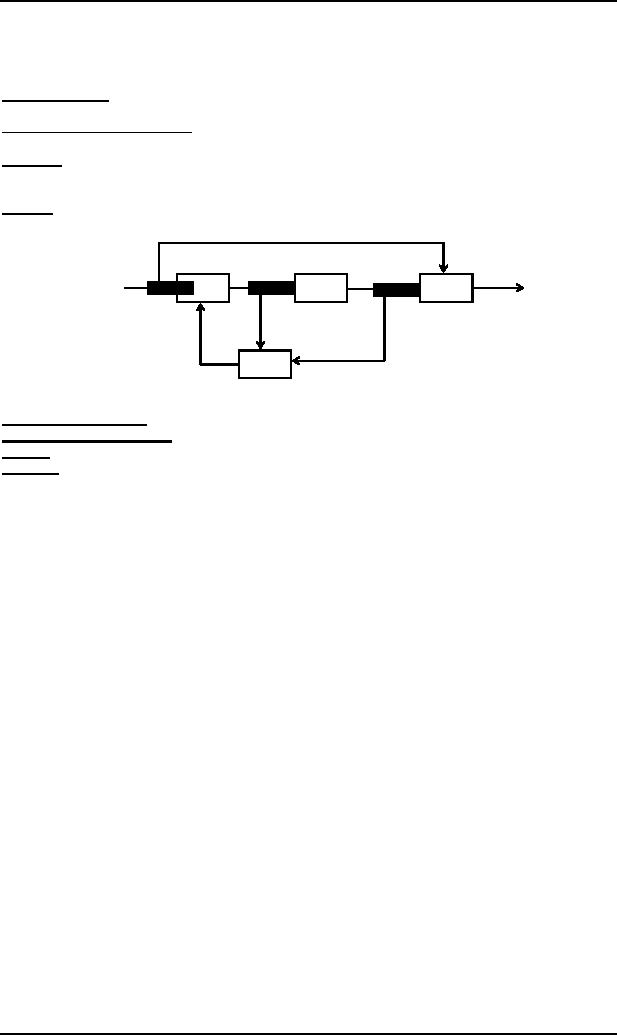
Consider
the following sequential
circuit
A
output
B
input
DELAY
OR
NAND
AND
The
following four types of
boxes are used in this
circuit
NAND
box (NOT AND): For
the given input, it provides
the complement of Boolean AND
output.
DELAY
box (Flip Flop
box): It
delays the transmission of signal along
the wire by one step (clock
pulse).
OR
box: For
the given input, it provides
the Boolean OR output.
AND
box: For
the given input, it provides
the Boolean AND
output.
The
current in the wire is indicated by 1 and
0 indicates the absence of
the current.
There
are two points A and B
w.r.t. to which following four
states of the machine are
identified according to the
presence
and absence of current at these
points i.e.
q0(A=0,
B=0) ∫ (0,0)
q1 (A=0,
B=1) ∫ (0,1)
q2 (A=1,
B=0) ∫ (1,0)
q3 (A=1,
B=1) ∫ (1,1)
The
operation of the circuit is
such that the machine
changes its state after
reading 0 or 1. The
transitions
are determined using the
following relations
new B =
old A
new A =
(input) NAND
(old A
AND
old
B)
output =
(input) OR (old
B)
It is to be
noted that old A and
old B indicate the presence or
absence of current at A and B before
inputting any
letter.
Similarly new A and new B
indicate the presence or absence of
current after reading certain letter.
At
various discrete pulses of a time
clock, input is received by
the machine and the
corresponding output string
is
generated.
The
transition at the state q0 after reading the letter 0,
can be determined, along
with the corresponding output
character
as under
new B =
old A = 0
new A =
(input) NAND
(old A
AND
old
B)
= 0 NAND
( 0
AND
0) = 0
NAND
0
=1
output =
(input) OR (old B) =
0 OR
0 =
0
Thus
after reading 0 at q0 new
B is 0 and new A is 1 i.e.
machine will be at state
(1,0) ∫ q2 and during
this
process
it's output character will be
0.
The
remaining action of this sequential
circuit can be determined as shown by the
following suggested transition
table of
the corresponding Mealy
machine
68
Theory of
Automata
(CS402)
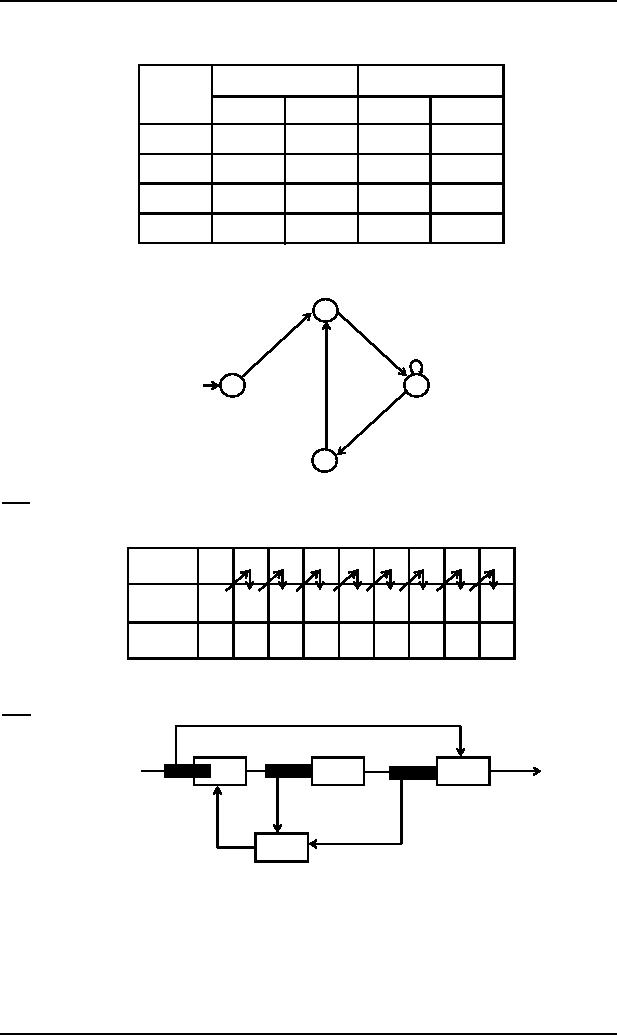
Inputting
0
Inputting
1
Old
state
State
Output
State
Output
q0 ∫(0,0)
(1,0)∫q2
(1,0)∫q2
0
1
q1 ∫(0,1)
(1,0)∫q2
(1,0)∫q2
1
1
q2 ∫(1,0)
(1,1)∫q3
(1,1)∫q3
0
1
q3 ∫(1,1)
(0,1)∫q1
(1,1)∫q3
1
1
The
corresponding transition diagram may be as
follows
q2
0/0,
1/1
0/0,
1/1
0/1
0/1
1/1
q3
q0
1/1
q1
Note: It
may be noted that if the
string 00 is read at any state, it
results in ending in state q3.
Running
the string 01101110 on the previous
machine, the output string can be
determined by the following
table
Input
0
1
1
0
1
1
1
0
States
q0
q2
q3
q1
q2
q3
q1
q2
q3
output
0
1
1
1
1
1
1
0
Following
is a note regarding the
sequential circuit under
consideration
Note
input
output
A
B
DELAY
OR
NAND
AND
It is to be
noted that in this
sequential circuit, delay box plays an
important role in introducing
four states of the
machine.
69
Table of Contents:
- What does automata mean, Introduction to languages
- Kleene Star Closure, Recursive definition of languages
- Regular Expression, Recursive definition of Regular Expression
- Equivalent Regular Expressions
- Finite Automaton
- Equivalent FAs
- FA corresponding to finite languages
- Examples of TGs: accepting all strings
- Generalized Transition Graphs
- Nondeterminism, Kleene’s Theorem
- Proof(Kleene’s Theorem Part II)
- Kleene’s Theorem Part III
- Concatenation of FAs
- Closure of an FA
- Nondeterministic Finite Automaton, Converting an FA to an equivalent NFA
- NFA with Null String
- NFA and Kleene’s Theorem
- NFA corresponding to Concatenation of FAs
- Distinguishable strings and Indistinguishable strings
- Finite Automaton with output, Moore machine
- Mealy machine
- Equivalent machines
- Mealy machines in terms of sequential circuit
- Regular languages, Complement of a language
- Nonregular languages
- Pumping Lemma
- Pumping Lemma version II
- Pseudo theorem
- Decidability
- finiteness of a language
- Context Free Grammar (CFG), CFG terminologies
- Trees
- Polish Notation (o-o-o)
- Total language tree, Regular Grammar
- Null Production
- Chomsky Normal Form (CNF)
- A new format for FAs
- Nondeterministic PDA
- PDA corresponding to CFG
- Conversion form of PDA
- Conversion Form, Joints of the machine
- Row language, Nonterminals
- Non-Context-Free language, Pumping lemma for CFLs
- Decidablity, Parsing Techniques
- Turing machine