 |

4
Bit
Manipulations
4.1.
MULTIPLICATION ALGORITHM
With
the important capability of
decision making in our repertoire we
move
on to
the discussion of an algorithm, which
will help us uncover an
important
set of instructions in our processor
used for bit
manipulations.
Multiplication
is a common process that we
use, and we were trained to
do
in
early schooling. Remember
multiplying by a digit and
then putting a cross
and
then multiplying with the
next digit and putting two
crosses and so on
and
summing the intermediate results in
the end. Very familiar
process but
we
never saw the process as an
algorithm, and we need to
see it as an
algorithm
to convey it to the
processor.
To
highlight the important
thing in the algorithm we
revise it on two 4bit
binary
numbers. The numbers are
1101 i.e. 13 and 0101
i.e. 5. The answer
should
be 65 or in binary 01000001. Observe
that the answer is twice
as
long as
the multiplier and the
multiplicand. The multiplication is
shown in
the
following figure.
1101 =
13
0101 =
5
-----
1101
0000x
1101xx
0000xxx
--------
01000001 =
65
We take
the first digit of the
multiplier and multiply it with
the
multiplicand.
As the digit is one the
answer is the multiplicand
itself. So we
place
the multiplicand below the
bar. Before multiplying with
the next digit a
cross
is placed at the right most
place on the next line
and the result is
placed
shifted one digit left.
However since the digit is
zero, the result is
zero.
Next
digit is one, multiplying with
which, the answer is 1101.
We put two
crosses
on the next line at the
right most positions and
place the result
there
shifted
two places to the left. The
fourth digit is zero, so the
answer 0000 is
placed
with three crosses to its
right.
Observe
the beauty of binary base,
as no real multiplication is needed
at
the
digit level. If the digit is
0 the answer is 0 and if the
digit is 1 the answer
is the
multiplicand itself. Also
observe that for every
next digit in the
multiplier
the answer is written
shifted one more place to
the left. No shifting
for
the first digit, once
for the second, twice
for the third and
thrice for the
fourth
one. Adding all the
intermediate answers the
result is 01000001=65
as
desired. Crosses are treated
as zero in this
addition.
Before
formulating the algorithm
for this problem, we need
some more
instructions
that can shift a number so
that we use this instruction
for our
multiplicand
shifting and also some way
to check the bits of the
multiplier
one by
one.
4.2.
SHIFTING AND
ROTATIONS
The
set of shifting and rotation
instructions is one of the
most useful set in
any
processor's instruction set.
They simplify really complex
tasks to a very
Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
neat
and concise algorithm. The
following shifting and
rotation operations
are
available in our processor.
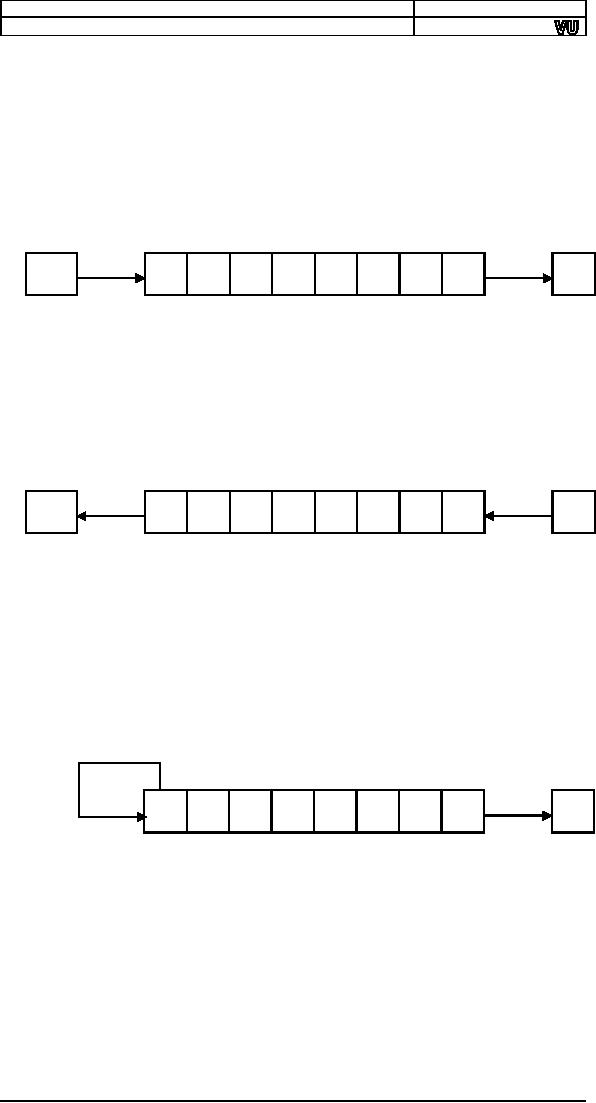
Shift
Logical Right
(SHR)
The
shift logical right
operation inserts a zero
from the left and
moves
every
bit one position to the
right and copies the
rightmost bit in the
carry
flag.
Imagine that there is a pipe
filled to capacity with eight
balls. The pipe is
open
from both ends and
there is a basket at the
right end to hold
anything
dropping
from there. The operation of
shift logical right is to
force a white
ball
from the left end.
The operation is depicted in
the following
illustration.
0
1
0
1
1
0
1
0
0
C
White
balls represent zero bits
while black balls represent
one bits. Sixteen
bit
shifting is done the same
way with a pipe of double
capacity.
Shift
Logical Left (SHL) / Shift
Arithmetic Left
(SAL)
The
shift logical left operation
is the exact opposite of
shift logical right.
In
this
operation the zero bit is
inserted from the right
and every bit moves
one
position
to its left with the most
significant bit dropping into
the carry flag.
Shift
arithmetic left is just
another name for shift
logical left. The operation
is
again
exemplified with the following
illustration of ball and
pipes.
C
1
0
1
1
0
1
0
0
0
Shift
Arithmetic Right
(SAR)
A
signed number holds the
sign in its most significant
bit. If this bit was
one a
logical right shifting will
change the sign of this
number because of
insertion
of a zero from the left.
The sign of a signed number
should not
change
because of shifting.
The
operation of shift arithmetic
right is therefore to shift
every bit one
place
to the right with a copy of
the most significant bit
left at the most
significant
place. The bit dropped from
the right is caught in the
carry
basket.
The sign bit is retained in
this operation. The
operation is further
illustrated
below.
1
0
1
1
0
1
0
0
C
The
left shifting operation is
basically multiplication by 2 while
the right
shifting
operation is division by two.
However for signed numbers
division by
two can
be accomplished by using shift
arithmetic right and not
shift logical
right.
The left shift operation is
equivalent to multiplication except when
an
important
bit is dropped from the
left. The overflow flag will
signal this
condition
if it occurs and can be
checked with JO. For division by 2 of
a
signed
number logical right
shifting will give a wrong
answer for a negative
number
as the zero inserted from
the left will change its
sign. To retain the
sign
flag and still effectively
divide by two the shift
arithmetic right
instruction
must be used on signed
numbers.
44
Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
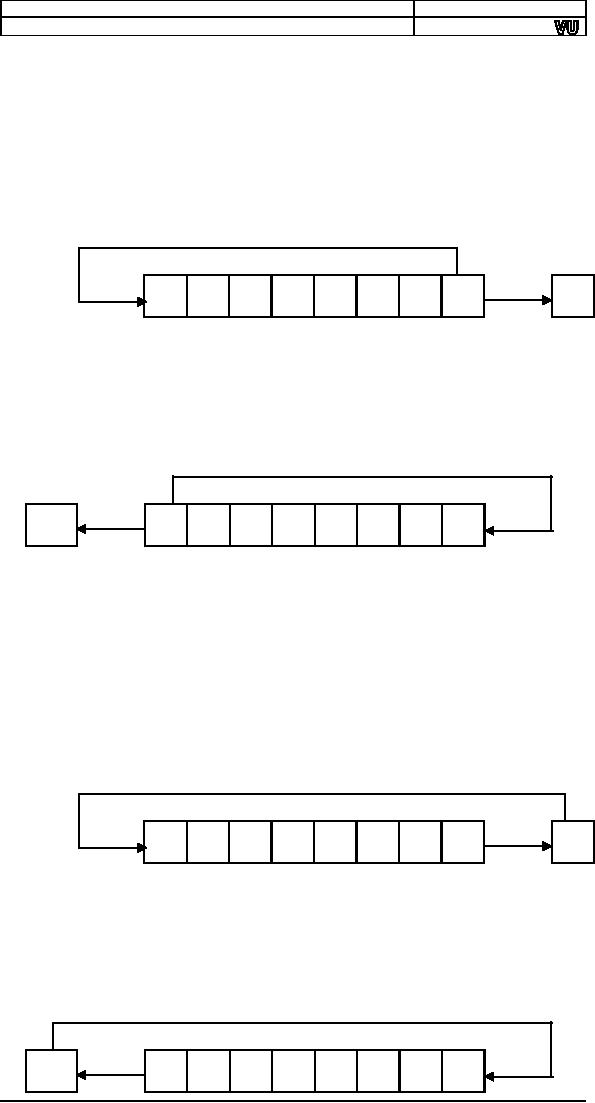
Rotate
Right (ROR)
In the
rotate right operation every
bit moves one position to
the right and
the bit
dropped from the right is
inserted at the left. This
bit is also copied
into
the carry flag. The
operation can be understood by
imagining that the
pipe
used for shifting has
been molded such that
both ends coincide.
Now
when
the first ball is forced to
move forward, every ball
moves one step
forward
with the last ball entering
the pipe from its
other end occupying
the
first
ball's old position. The
carry basket takes a
snapshot of this ball
leaving
one
end of the pipe and
entering from the
other.
1
0
1
1
0
1
0
0
C
Rotate
Left (ROL)
In the
operation of rotate left
instruction, the most
significant bit is copied
to the
carry flag and is inserted
from the right, causing
every bit to move one
position
to the left. It is the
reverse of the rotate right
instruction. Rotation
can be
of eight or sixteen bits.
The following illustration will
make the
concept
clear using the same
pipe and balls
example.
C
1
0
1
1
0
1
0
0
Rotate
Through Carry Right
(RCR)
In the
rotate through carry right
instruction, the carry flag
is inserted from
the
left, every bit moves one
position to the right, and
the right most bit is
dropped
in the carry flag.
Effectively this is a nine bit or a
seventeen bit
rotation
instead of the eight or
sixteen bit rotation as in the
case of simple
rotations.
Imagine
the circular molded pipe as
used in the simple rotations
but this
time
the carry position is part
of the circle between the
two ends of the pipe.
Pushing
the carry ball from
the left causes every
ball to move one step to
its
right
and the right most bit
occupying the carry place.
The idea is further
illustrated
below.
1
0
1
1
0
1
0
0
C
Rotate
Through Carry Left
(RCL)
The
exact opposite of rotate
through carry right
instruction is the
rotate
through
carry left instruction. In
its operation the carry
flag is inserted from
the
right causing every bit to
move one location to its
left and the
most
significant
bit occupying the carry
flag. The concept is
illustrated below in
the
same manner as in the last
example.
C
1
0
1
1
0
1
0
0
45

Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
4.3.
MULTIPLICATION IN ASSEMBLY
LANGUAGE
In the
multiplication algorithm discussed
above we revised the way
we
multiplied
number in lower classes, and
gave an example of that
method on
binary
numbers. We make a simple
modification to the traditional
algorithm
before
we proceed to formulate it in assembly
language.
In the
traditional algorithm we calculate
all intermediate answers and
then
sum them to
get the final answer. If we
add every intermediate
answer to
accumulate
the result, the result will
be same in the end, except
that we do
not
have to remember a lot of
intermediate answers during
the whole
multiplication.
The multiplication with the new
algorithm is shown
below.
1101
=
13
Accumulated
Result
0101
=
5
-----
0 (Initial
Value)
1101
=
13
0 + 13
=
13
0000x
=
0
13 + 0
=
13
1101xx
=
52
13 + 52
=
65
0000xxx
=
0
65 + 0
=
65
(Answer)
We try to
identify steps of our algorithm.
First we set the result to
zero.
Then we
check the right most bit of
multiplier. If it is one add
the
multiplicand
to the result, and if it is
zero perform no addition.
Left shift the
multiplicand
before the next bit of
multiplier is tested. The
left shifting of the
multiplicand
is performed regardless of the
value of the multiplier's
right
most
bit. Just like the crosses
in traditional multiplication are
always placed
to mark
the ones, tens, thousands,
etc. places. Then check
the next bit and if
it is
one add the shifted
value of the multiplicand to
the result. Repeat for
as
many
digits as there are in the
multiplier, 4 in our example. Formulating
the
steps
of the algorithm we
get:
· Shift
the multiplier to the
right.
· If
CF=1 add the multiplicand to
the result.
· Shift
the multiplicand to the
right.
· Repeat
the algorithm 4
times.
For an
8bit multiplication the
algorithm will be repeated 8 times
and for a
sixteen
bit multiplication it will be repeated 16
times, whatever the size of
the
multiplier
is.
The
algorithm uses the fact
that shifting right forces
the right most bit to
drop in
the carry flag. If we test
the carry flag using JC we
are effectively
testing
the right most bit of the
multiplier. Another shifting will
cause the
next
bit to drop in the next
iteration and so on. So our
task of checking bits
one by
one is satisfied using the
shift operation. There are
many other
methods
to do this bit testing as well,
however we exemplify one of
the
methods
in this example.
In the
first iteration there is no
shifting just like there is
no cross in
traditional
multiplication in the first
pass. Therefore we placed
the left
shifting
of the multiplicand after
the addition step. However
the right shifting
of
multiplier must be before the
addition as the addition
step's execution
depends
upon its result.
We
introduce an assembly language
program to perform this
4bit
multiplication.
The algorithm is extensible to
more bits but there are a
few
complications,
which are left to be discussed
later. For now we do a
4bit
multiplication
to keep the algorithm
simple.
Example
4.1
01
; 4bit multiplication
algorithm
02
[org
0x100]
03
jmp
start
04
05
multiplicand:
db
13
; 4bit multiplicand (8bit
space)
06
multiplier:
db
5
; 4bit
multiplier
46

Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
07
result:
db
0
; 8bit
result
08
09
start:
mov
cl, 4
; initialize bit count to
four
10
mov
bl, [multiplicand] ; load
multiplicand in bl
11
mov
dl,
[multiplier]
; load multiplier in
dl
12
13
checkbit:
shr
dl, 1
; move right
most bit in carry
14
jnc
skip
; skip addition if bit is
zero
15
16
add
[result],
bl
; accumulate
result
17
18
skip:
shl
bl, 1
; shift multiplicand
left
19
dec
cl
; decrement bit
count
20
jnz
checkbit
; repeat if bits
left
21
22
mov
ax,
0x4c00
; terminate
program
23
int
0x21
The
numbers to be multiplied are
constants for now.
The
04-06
multiplication
is four bit so the answer is
stored in an 8bit
register.
If the
operands were 8bit the
answer would be 16bit and if
the
07
operands
were 16bit the answer
would be 32bit. Since eight
bits can
fit in
a byte we have used 4bit
multiplication as our first
example.
Since
addition by zero means
nothing we skip the addition
step if
14-16
the
rightmost bit of the multiplier is
zero. If the jump is not
taken
the
shifted value of the
multiplicand is added to the
result.
The
multiplicand is left shifted in
every iteration regardless of
the
18
multiplier
bit.
DEC is a new
instruction but its operation
should be immediately
19
understandable
with the knowledge gained
till now. It simply
subtracts
one from its single
operand.
The JNZ
instruction causes the
algorithm to repeat till any
bits of
20
the
multiplier are left
Inside
the debugger observe the
working of the SHR and SHL
instructions.
The SHR
instruction is effectively dividing
its operand by two and
the
remainder
is stored in the carry flag
from where we test it.
The SHL
instruction
is multiplying its operand by two so
that it is added at one
place
more
towards the left in the
result.
4.4.
EXTENDED OPERATIONS
We
performed a 4bit multiplication to
explain the algorithm
however the
real
advantage of the computer is when we
ask it to multiply large
numbers,
Numbers
whose multiplication takes
real time. If we have an
8bit number we
can do
the multiplication in word
registers, but are we limited to
word
operations?
What if we want to multiply 32bit or
even larger numbers?
We
are
certainly not limited.
Assembly language only
provides us the basic
building
blocks. We build a plaza out of
these blocks, or a building, or
a
classic
piece of architecture is only
dependant upon our imagination.
With
our
logic we can extend these
algorithms as much as we want.
Our
next example will be multiplication of
16bit numbers to produce
a
32bit
answer. However for a 32bit
answer we need a way to shift a
32bit
number
and a way to add 32bit
numbers. We cannot depend on
16bit
shifting
as we have 16 significant bits in our
multiplicand and shifting
any
bit
towards the left may drop a
valuable bit causing a totally
wrong result. A
valuable
bit means any bit that is
one. Dropping a zero bit
doesn't cause any
difference.
So we place the 16it number
in 32bit space with the
upper 16 bits
zeroed
so that the sixteen shift
operations don't cause any
valuable bit to
drop.
Even though the numbers
were 16bit we need 32bit
operations to
multiply
correctly.
To
clarify this necessity, we
take example of a number
40000 or 9C40 in
hexadecimal.
In binary it is represented as
1001110001000000. To multiply
47
Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
by two we
shift it one place to the
left. The answer we get
is
0011100010000000
and the left most
one is dropped in the carry
flag. The
answer
should be the 17bit number
0x13880 but it is 0x3880, which
are
14464
in decimal instead of the
expected 80000. We should be
careful of this
situation
whenever shifting is
used.
Extended
Shifting
Using
our basic shifting and
rotation instructions we can
effectively shift a
32bit
number in memory word by
word. We cannot shift the
whole number
at once
since our architecture is limited to
word operations. The
algorithm
we use
consists of just two instructions
and we name it extended
shifting.
num1:
dd
40000
shl
word [num1],
1
rcl
word [num1+2],
1
The DD
directive reserves a 32bit
space in memory, however the
value we
placed
there will fit in 16bits. So we
can safely shift the
number left 16 times.
The
least significant word is
accessible at num1 and the
most significant
word is
accessible at num1+2.
The two
instructions are carefully
crafted such that the
first one shifts
the
lower
word towards the left
and the most significant bit
of that word is
dropped
in carry. With the next
instruction we push that
dropped bit into the
least
significant bit of the next
word effectively joining the
two 16bit words.
The
final carry after the
second instruction will be the
most significant bit of
the
higher word, which for this
number will always be
zero.
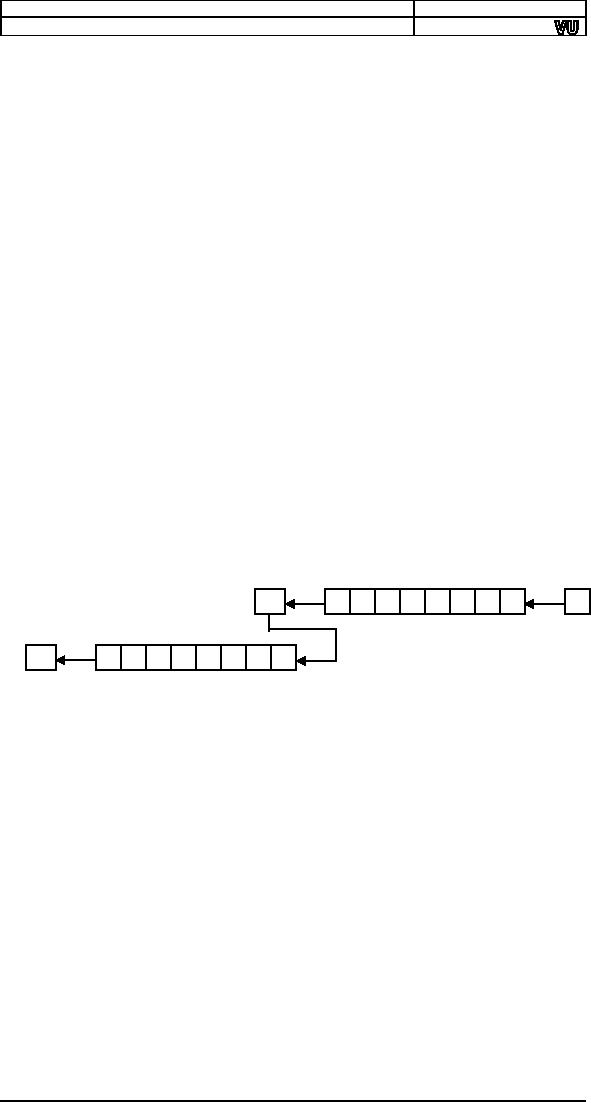
The
following illustration will clarify
the concept. The pipe on
the right
contains
the lower half and
the pipe on the left
contains the upper half.
The
first
instruction forced a zero
from the right into
the lower half and
the left
most
bit is saved in carry, and
from there it is pushed into
the upper half
and
the upper half is shifted as
well.
C
10110100
0
Step
1
Step
2
C
10110100
For
shifting right the exact
opposite is done however
care must be taken to
shift
right the upper half
first and then rotate
through carry right the
lower
half
for obvious reasons. The
instructions to do this
are.
num1:
dd
40000
shr
word [num1+2],
1
rcr
word [num1],
1
The
same logic has worked.
The shift placed the
least significant bit of
the
upper
half in the carry flag
and it was pushed from right
into the lower
half.
For a
singed shift we would have
used the shift arithmetic
right instruction
instead
of the shift logical right
instruction.
The
extension we have done is
not limited to 32bits. We
can shift a number
of any
size say 1024 bits.
The second instruction will be
repeated a number
of
times and we can achieve
the desired effect. Using
two simple instructions
we have
increased the capability of
the operation to effectively an
unlimited
number
of bits. The actual limit is
the available memory as even
the segment
limit
can be catered with a little
thought.
Extended Addition
and Subtraction
We also
needed 32bit addition for
multiplication of 16bit numbers.
The
idea of
extension is same here.
However we need to introduce a
new
instruction
at this place. The
instruction is ADC or "add with carry."
Normal
addition
has two operands and the
second operand is added to
the first
48

Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
operand.
However ADC has three
operands. The third implied
operand is the
carry
flag. The ADC instruction is
specifically placed for
extending the
capability
of ADD. Numbers of any size
can be added using a
proper
combination
of ADD and ADC. All basic
building blocks are provided
for the
assembly
language programmer, and the
programmer can extend
its
capabilities
as much as needed by using these
fine instructions in
appropriate
combinations.
Further
clarifying the operation of
ADC, consider an instruction
"ADC AX,
BX."
Normal addition would have
just added BX to AX, however ADC
first
adds
the carry flag to AX and
then adds BX to AX. Therefore
the last carry is
also
included in the
result.
The
algorithm should be apparent by
now. The lower halves of
the two
numbers
to be added are first added
with a normal addition. For
the upper
halves
a normal addition would lose
track of a possible carry
from the lower
halves
and the answer would be
wrong. If a carry was generated it
should go
to the
upper half. Therefore the
upper halves are added with
an addition with
carry
instruction.
Since
one operand must be in register, ax is
used to read the lower
and
upper
halves of the source one by
one. The destination is
directly updated.
The
set of instructions goes
here.
dest:
dd
40000
src:
dd
80000
mov
ax, [src]
add
word [dest],
ax
mov
ax, [src+2]
adc
word [dest+2],
ax
To
further extend it more
addition with carries will be used.
However the
carry
from last addition will be
wasted as there will always be a
size limit
where
the results and the
numbers are stored. This
carry will remain in
the
carry
flag to be tested for a
possible overflow.
For
subtraction the same logic
will be used and just like
addition with
carry
there is an instruction to subtract with
borrows called SBB. Borrow
in
the
name means the carry
flag and is used just
for clarity. Or we can
say
that
the carry flag holds
the carry for addition
instructions and the
borrow
for
subtraction instructions. Also
the carry is generated at
the 17th bit and
the
borrow is also taken from
the 17th bit. Also
there is no single
instruction
that
needs borrow and carry in
their independent meanings at
the same
time.
Therefore it is logical to use
the same flag for
both tasks.
We
extend subtraction with a very
similar algorithm. The lower
halves
must be
subtracted normally while
the upper halves must be
subtracted with
a
subtract with borrow instruction so
that if the lower halves
needed a
borrow,
a one is subtracted from the
upper halves. The algorithm
is as
under.
dest:
dd
40000
src:
dd
80000
mov
ax, [src]
sub
word [dest],
ax
mov
ax, [src+2]
sbb
word [dest+2],
ax
Extended
Multiplication
We use
extended shifting and
extended addition to formulate our
algorithm
to do
extended multiplication. The
multiplier is still stored in
16bits since we
only
need to check its bits
one by one. The multiplicand
however cannot be
stored
in 16bits otherwise on left
shifting its significant
bits might get
lost.
Therefore
it has to be stored in 32bits
and the shifting and
addition used to
accumulate
the result must be 32bits as
well.
Example
4.2
49

Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
01
; 16bit
multiplication
02
[org
0x0100]
03
jmp
start
04
05
multiplicand:
dd
1300
; 16bit multiplicand 32bit
space
06
multiplier:
dw
500
; 16bit
multiplier
07
result:
dd
0
; 32bit
result
08
09
start:
mov
cl, 16
; initialize bit count to
16
10
mov
dx,
[multiplier]
; load multiplier in
dx
11
12
checkbit:
shr
dx, 1
; move right
most bit in carry
13
jnc
skip
; skip addition if bit is
zero
14
15
mov
ax,
[multiplicand]
16
add
[result],
ax
; add less
significant word
17
mov
ax,
[multiplicand+2]
18
adc
[result+2],
ax
; add
more significant word
19
20
skip:
shl
word
[multiplicand], 1
21
rcl
word
[multiplicand+2], 1 ; shift multiplicand left
22
dec
cl
; decrement bit
count
23
jnz
checkbit
; repeat if bits
left
24
25
mov
ax,
0x4c00
; terminate
program
26
int
0x21
The
multiplicand and the
multiplier are stored in
32bit space while
05-07
the
multiplier is stored as a
word.
10
The
multiplier is loaded in DX where it will
be shifted bit by bit. It
can be
directly shifted in memory as
well.
15-18
The
multiplicand is added to the
result using extended
32bit
addition.
20-21
The
multiplicand is shifted left as a
32bit number using
extended
shifting
operation.
The
multiplicand will occupy the
space from 0103-0106, the
multiplier will
occupy
space from 0107-0108 and
the result will occupy the
space from
0109-010C.
Inside the debugger observe
the changes in these
memory
locations
during the course of the
algorithm. The extended
shifting and
addition
operations provide the same
effect as would be provided if
there
were
32bit addition and shifting
operations available in the
instruction set.
At the
end of the algorithm the
result memory locations
contain the value
0009EB10
which is 65000 in decimal; the
desired answer. Also observe
that
the
number 00000514 which is 1300 in
decimal, our multiplicand,
has
become
05140000 after being left
shifted 16 times. Our extended
shifting has
given
the same result as if a
32bit number is left shifted
16 times as a unit.
There
are many other important
applications of the shifting
and rotation
operations
in addition to this example of
the multiplication algorithm.
More
examples
will come in coming
chapters.
4.5.
BITWISE LOGICAL
OPERATIONS
The
8088 processor provides us with a
few logical operations that
operate
at the
bit level. The logical
operations are the same as
discussed in computer
logic
design; however our perspective will be a
little different. The four
basic
operations
are AND, OR, XOR,
and NOT.
The
important thing about these
operations is that they are
bitwise. This
means
that if "and ax, bx"
instruction is given, then
the operation of AND is
applied
on corresponding bits of AX and BX.
There are 16 AND operations
as
a
result; one for every bit of
AX. Bit 0 of AX will be set if both its
original
value
and Bit 0 of BX are set, bit 1 will be
set if both its original
value and
Bit 1 of BX
are set, and so on for
the remaining bits. These
operations are
conducted
in parallel on the sixteen
bits. Similarly the
operations of other
logical
operations are bitwise as
well.
50
Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
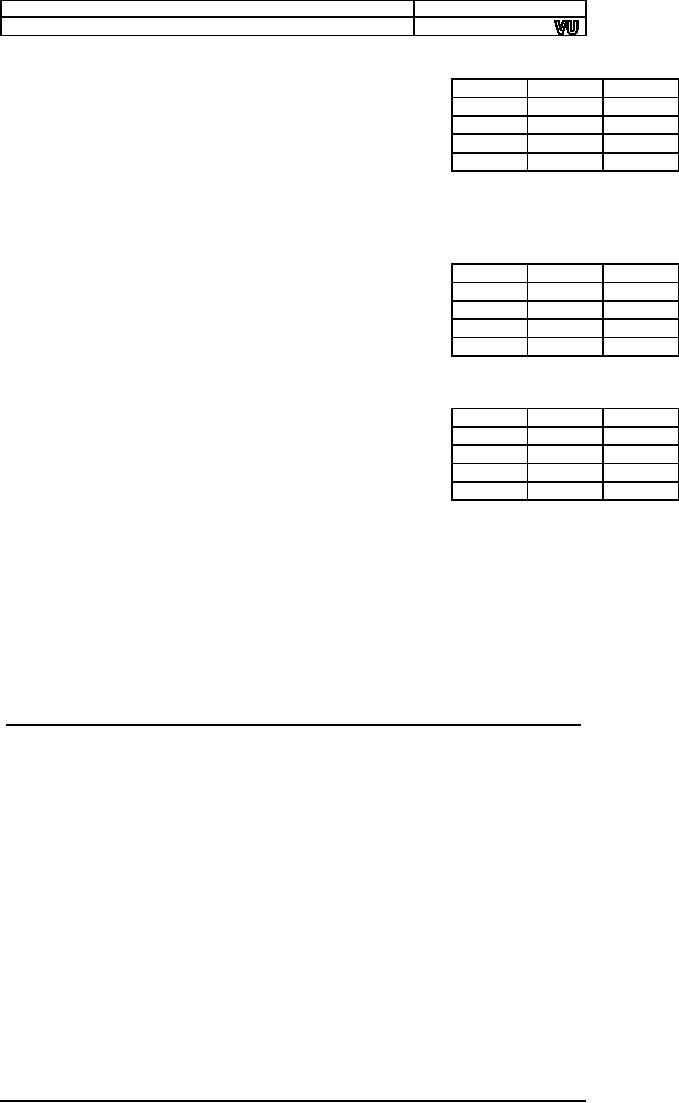
AND
operation
AND
performs the logical bitwise
and
of
the two
X
Y
X and
Y
operands
(byte or word) and returns
the result to the
0
0
0
destination
operand. A bit in the result is
set if both
0
1
0
corresponding
bits of the original
operands are set;
1
0
0
otherwise
the bit is cleared as shown in
the truth table.
1
1
1
Examples
are "and ax, bx" and
"and byte [mem], 5."
All
possibilities
that are legal for
addition are also legal
for the AND
operation.
The
different thing is the
bitwise behavior of this
operation.
OR
operation
OR
performs the logical bitwise
"inclusive or" of the
two
X
Y
X or
Y
operands
(byte or word) and returns
the result to the
0
0
0
destination
operand. A bit in the result is
set if either or
0
1
1
both
corresponding bits in the
original operands are
set
1
0
1
otherwise
the result bit is cleared as
shown in the truth
1
1
1
table.
Examples are "or ax, bx"
and "or byte [mem],
5."
XOR
operation
XOR
(Exclusive Or) performs
the logical
bitwise
X
Y
X xor
Y
"exclusive
or" of the two operands and
returns the result
0
0
0
to the
destination operand. A bit in the
result is set if the
0
1
1
corresponding
bits of the original
operands contain
1
0
1
opposite
values (one is set, the
other is cleared)
otherwise
1
1
0
the
result bit is cleared as shown in
the truth table. XOR
is a
very important operation due
to the property that it is a
reversible
operation.
It is used in many cryptography
algorithms, image processing,
and
in
drawing operations. Examples
are "xor ax, bx" and
"xor byte [mem],
5."
NOT
operation
NOT
inverts the bits (forms
the one's complement) of the
byte or word
operand.
Unlike the other logical
operations, this is a single
operand
instruction,
and is not purely a logical
operation in the sense the
others are,
but it is
still traditionally counted in
the same set. Examples
are "not ax"
and
"not
byte [mem], 5."
4.6.
MASKING OPERATIONS
Selective
Bit Clearing
Another
use of AND is to make selective
bits zero in its
destination
operand.
The source operand is loaded
with a mask containing one at
positions
which are retain their old
value and zero at positions
which are to
be
zeroed. The effect of
applying this operation on
the destination with mask
in the
source is to clear the
desired bits. This operation
is called masking.
For
example if the lower nibble
is to be cleared then the
operation can be
applied
with F0 in the source. The
upper nibble will retain its
old value and
the
lower nibble will be
cleared.
Selective
Bit Setting
The
operation can be used as a
masking operation to set
selective bits. The
bits in
the mask are cleared at
positions which are to retain
their values, and
are
set at positions which are to be
set. For example to set
the lower nibble of
the
destination operand, the
operation should be applied with a mask
of 0F
in the
source. The upper nibble
will retain its value and
the lower nibble will
be set
as a result.
51

Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
Selective
Bit Inversion
XOR can
also be used as a masking
operation to invert selective
bits. The
bits in
the mask are cleared at
positions, which are to retain
their values,
and
are set at positions, which
are to be inverted. For
example to invert the
lower
nibble of the destination
operand, the operand should
be applied with
a mask of 0F in
the source. The upper
nibble will retain its value
and the
lower
nibble will be set as a result.
Compare this with NOT which
inverts
everything.
XOR on the other hand allows
inverting selective
bits.
Selective
Bit Testing
AND can
be used to check whether
particular bits of a number
are set or
not.
Previously we used shifting
and JC to test bits one by
one. Now we
introduce
another way to test bits, which is
more powerful in the sense
that
any bit
can be tested anytime and
not necessarily in order. AND
can be
applied
on a destination with a 1-bit in the
desired position and a
source,
which is to be
checked. If the destination is
zero as a result, which can
be
checked
with a JZ instruction, the bit at the
desired position in the
source
was
clear.
However
the AND operation destroys
the destination mask, which
might be
needed
later as well. Therefore
Intel provided us with another
instruction
analogous
to CMP, which is non-destructive
subtraction. This is the
TEST
instruction
and is a non-destructive AND operation.
It doesn't change the
destination
and only sets the
flags according to the AND
operation. By
checking
the flags, we can see if
the desired bit was set or
cleared.
We
change our multiplication algorithm to
use selective bit testing
instead
of
checking bits one by one
using the shifting
operations.
Example
4.3
01
; 16bit multiplication using
test for bit testing
02
[org
0x0100]
03
jmp
start
04
05
multiplicand:
dd
1300
; 16bit multiplicand 32bit
space
06
multiplier:
dw
500
; 16bit
multiplier
07
result:
dd
0
; 32bit
result
08
09
start:
mov
cl, 16
; initialize bit count to
16
10
mov
bx, 1
; initialize bit
mask
11
12
checkbit:
test bx,
[multiplier]
; move right
most bit in carry
13
jz
skip
; skip addition if bit is
zero
14
15
mov
ax,
[multiplicand]
16
add
[result],
ax
; add less
significant word
17
mov
ax,
[multiplicand+2]
18
adc
[result+2],
ax
; add
more significant word
19
20
skip:
shl
word
[multiplicand], 1
21
rcl
word
[multiplicand+2], 1 ; shift multiplicand left
22
shl
bx, 1
; shift mask
towards next bit
23
dec
cl
; decrement bit
count
24
jnz
checkbit
; repeat if bits
left
25
26
mov
ax,
0x4c00
; terminate
program
27
int
0x21
The
test instruction is used for
bit testing. BX holds the mask
and in
12
every
next iteration it is shifting
left, as our concerned bit is now
the
next
bit.
22-24
We can
do without counting in this
example. We can stop as soon
as
our mask in BX
becomes zero. These are
the small tricks
that
assembly
allows us to do and optimize our
code as a result.
52

Computer
Architecture & Assembly Language
Programming
Course
Code: CS401
CS401@vu.edu.pk
Inside
the debugger observe that
both the memory location
and the mask in
BX do
not change as a result of
TEST instruction. Also
observe how our
mask is
shifting towards the left so
that the next TEST
instruction tests the
next
bit. In the end we get
the same result of 0009EB10
as in the previous
example.
EXERCISES
1.
Write a program to swap
every pair of bits in the AX
register.
2. Give
the value of the AX register
and the carry flag
after each of the
following
instructions.
stc
mov
ax, <your
rollnumber>
adc
ah, <first character of your
name>
cmc
xor
ah,
al
mov
cl,
4
shr
al,
cl
rcr
ah,
cl
3.
Write a program to swap the
nibbles in each byte of the
AX register.
4.
Calculate the number of one
bits in BX and complement an
equal
number
of least significant bits in
AX.
HINT:
Use the XOR
instruction
5.
Write a program to multiply two
32bit numbers and store
the answer
in a
64bit location.
6.
Declare a 32byte buffer
containing random data.
Consider for this
problem
that the bits in these 32
bytes are numbered from 0 to
255.
Declare
another byte that contains
the starting bit number.
Write a
program
to copy the byte starting at
this starting bit number in
the AX
register.
Be careful that the starting
bit number may not be a
multiple
of 8
and therefore the bits of
the desired byte will be
split into two
bytes.
7. AX
contains a number between
0-15. Write code to
complement the
corresponding
bit in BX. For example if AX contains 6;
complement the
6th bit of
BX.
8. AX
contains a non-zero number.
Count the number of ones in
it and
store
the result back in AX.
Repeat the process on the
result (AX) until
AX
contains one. Calculate in BX
the number of iterations it
took to
make AX
one. For example BX should
contain 2 in the following
case:
AX =
1100 0101 1010 0011
(input 8 ones)
AX =
0000 0000 0000 1000
(after first iteration 1
one)
AX =
0000 0000 0000 0001
(after second iteration 1
one) STOP
53
Table of Contents:
- Introduction to Assembly Language Programming
- Addressing Modes: Data Declaration, Direct, Register Indirect , Offset Addressing
- Branching: Comparison and Conditions, Conditional ,Unconditional Jump
- Manipulations: Multiplication Algorithm, Shifting and Rotations, Bitwise Logical Operations
- Subroutines: Program Flow, Stack, Saving and Restoring Registers
- Display Memory: ASCII Codes, Display Memory Formation, Assembly Language
- String Instructions: String Processing, Clearing Screen, String Printing, Length
- Software Interrupts: Hooking an Interrupt, BIOS and DOS Interrupts
- Real Time Interrupts and Hardware Interfacing
- Debug Interrupts: Debugger using single step interrupt, breakpoint interrupt
- Multitasking: Concept, Elaborate, Multitasking Kernel as TSR
- Video Services: BIOS Video Services, DOS Video Services
- Secondary Storage: Storage Access Using BIOS, DOS, Device Drivers
- Serial Port Programming: Serial Communication
- Protected Mode Programming: VESA Linear Frame Buffer, Interrupt Handling
- Interfacing with High Level Languages: Calling Conventions, Calling C from Assembly
- Comparison: Motorolla 68K Processors, Sun SPARC Processor