 |
Knowledge Representation and Reasoning |
| << Genetic Algorithms |
| Expert Systems >> |
Artificial
Intelligence (CS607)
Lecture No. 14
-17
4 Knowledge Representation and
Reasoning
Now that
have looked at general
problem solving, lets look
at knowledge
representation and
reasoning which are
important aspects of any
artificial
intelligence
system and of any computer system in
general. In this section we
will
become
familiar with classical
methods of knowledge representation
and
reasoning in
AI.
4.1
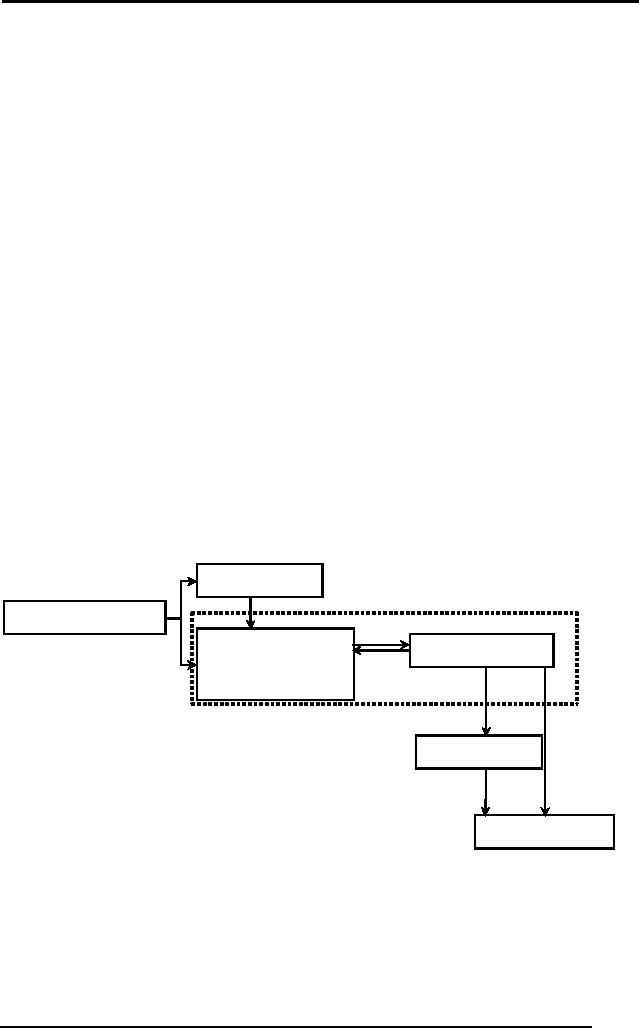
The AI Cycle
Almost
all AI systems have the
following components in
general:
· Perception
· Learning
· Knowledge
Representation and Reasoning
· Planning
· Execution
Figure 1
shows the relationship
between these
components.
An AI system
has a perception component
that allows the system to
get
information
from its environment. As
with human perception, this
may be visual,
audio or
other forms of sensory
information. The system must
then form a
meaningful and
useful representation of this
information internally.
This
knowledge
representation maybe static or it may be
coupled with a
learning
component
that is adaptive and draws
trends from the perceived
data.
LEARNING
PERCEPTION
KNOWLEDGE
REASONING
REPRESENTATION
(KR)
PLANNING
EXECUTION
Figure 1: The AI
Cycle
Knowledge
representation (KR) and
reasoning are closely
coupled components;
each is
intrinsically tied to the
other. A representation scheme is
not meaningful
on its
own; it must be useful and
helpful in achieve certain
tasks. The same
information may be
represented in many different
ways, depending on how
you
want to
use that information. For
example, in mathematics, if we want to
solve
89

Artificial
Intelligence (CS607)
problems
about ratios, we would most
likely use algebra, but we
could also use
simple
hand drawn symbols. To say
half of something, you could
use 0.5x or you
could
draw a picture of the object
with half of it colored
differently. Both
would
convey
the same information but
the former is more compact
and useful in
complex
scenarios where you want to
perform reasoning on the
information. It is
important at
this point to understand how
knowledge representation and
reasoning
are interdependent components,
and as AI system designer,
you have
to consider
this relationship when
coming up with any
solution.
4.2
The dilemma
The key question
when we begin to think about
knowledge representation and
reasoning is how
to approach the problem
----should we try to emulate
the human
brain
completely and exactly as it
is? Or should we come up
with something
new?
Since we do
not know how the KR and
reasoning components are
implemented
in humans,
even though we can see
their manifestation in the
form of intelligent
behavior, we
need a synthetic (artificial) way to
model the knowledge
representation and
reasoning capability of humans in
computers.
4.3
Knowledge and its types
Before we go any
further, lets try to
understand what `knowledge'
is. Durkin refers
to it as the
"Understanding of a subject area". A
well-focused subject area
is
referred to as a
knowledge domain, for
example, medical domain,
engineering
domain,
business domain,
etc..
If we analyze
the various types of
knowledge we use in every day
life, we can
broadly
define knowledge to be one of
the following
categories:
Procedural
knowledge: Describes how to do things,
provides a set of
·
directions of
how to perform certain
tasks, e.g., how to drive a
car.
Declarative
knowledge: It describes objects,
rather than processes.
What
·
is known
about a situation, e.g. it is
sunny today, and cherries
are red.
Meta knowledge:
Knowledge about knowledge,
e.g., the knowledge
that
·
blood
pressure is more important
for diagnosing a medical
condition than
eye
color.
Heuristic
knowledge: Rule-of-thumb, e.g. if I
start seeing shops, I am
close
·
to the
market.
o Heuristic
knowledge is sometimes called
shallow knowledge.
o Heuristic
knowledge is empirical as opposed to
deterministic
Structural
knowledge: Describes structures and
their relationships.
e.g.
·
how
the various parts of the
car fit together to make a
car, or knowledge
structures in
terms of concepts, sub
concepts, and objects.
90
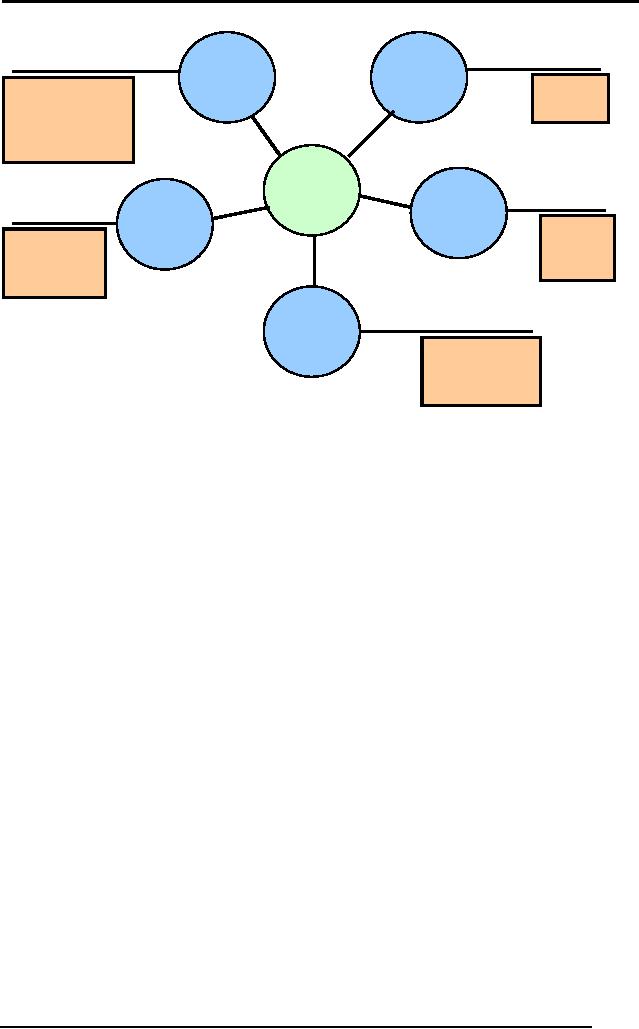
Artificial
Intelligence (CS607)
Structural
Declarative
Knowledge
Knowledge
Objects
Relationships
Facts
between
Objects,
Concepts
Knowledge
Heuristic
Procedural
Knowledge
Rules
Knowledge
Rules
of
Procedure
Thumb
s
Methods
Meta-
Knowledge
Knowledge
about
Knowledge
Fig 2:
Types of Knowledge
4.4
Towards Representation
There
are multiple approaches and
schemes that come to mind
when we begin to
think
about representation
Pictures and
symbols. This is how the
earliest humans
represented
knowledge
when sophisticated linguistic
systems had not yet
evolved
Graphs and
Networks
Numbers
4.4.1
Pictures
Each
type of representation has
its benefits. What types of
knowledge is best
represented
using pictures? , e.g. can
we represent the relationship
between
individuals in a
family using a picture? We
could use a series of
pictures to store
procedural
knowledge, e.g. how to boil
an egg. But we can easily
see that
pictures
are best suited for
recognition tasks and for
representing structural
information.
However, pictorial representations
are not very easily
translated to
useful
information in computers because
computers cannot interpret
pictures
directly
with out complex reasoning.
So even though pictures are
useful for
human
understanding, because they
provide a high level view of
a concept to be
obtained
readily, using them for
representation in computers is not as
straight
forward.
4.4.2 Graphs and
Networks
91
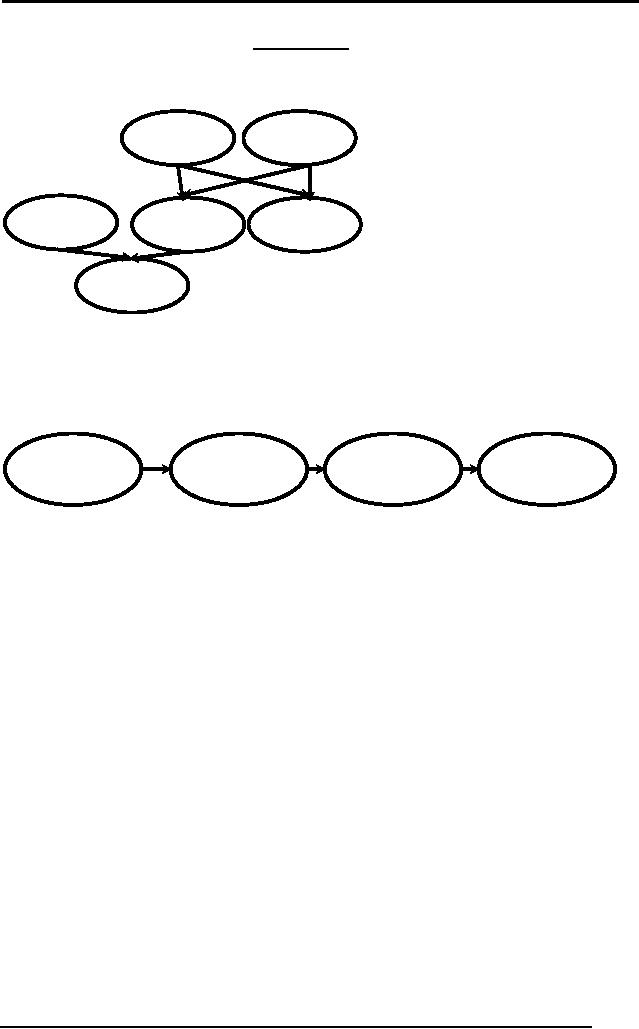
Artificial
Intelligence (CS607)
Graphs and
Networks allow relationships
between
objects/entities to be
incorporated,
e.g., to show family
relationships, we can use a
graph.
Tariq
Ayesha
Hassan
Amina
Mona
Ali
Fig 3:
Family Relationships
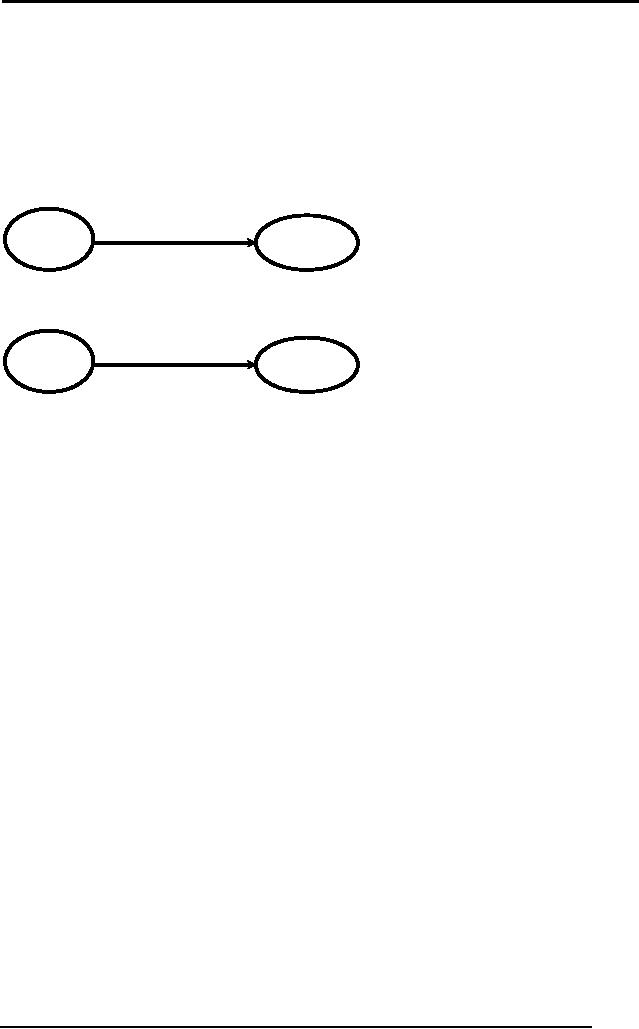
We can
also represent procedural
knowledge using graphs, e.g.
How to start a
car?
Insert
Key
Turn
Ignition
Press
Clutch
Set
Gear
Fig 4:
Graph for procedural
knowledge
4.4.3
Numbers
Numbers
are an integral part of
knowledge representation used by
humans.
Numbers
translate easily to computer
representation. Eventually, as we
know,
every
representation we use gets
translated to numbers in the
computers internal
representation.
4.4.4 An
Example
In the
context of the above
discussion, let's look at
some ways to represent
the
knowledge of a
family
Using a
picture
92
Artificial
Intelligence (CS607)
Fig 5:
Family Picture
As you
can see, this kind of
representation makes sense
readily to humans, but
if
we give
this picture to a computer, it
would not have an easy
time figuring out
the
relationships
between the individuals, or
even figuring out how
many individuals
are
there in the picture.
Computers need complex
computer vision algorithms
to
understand
pictures.
Using a
graph
Ayesha
Tariq
Mona
Fig 6:
Family graph
This
representation is more direct and
highlights relationships.
Using a
description in words
For
the family above, we could
say in words
Tariq is
Mona's Father
Ayesha is
Mona's Mother
Mona is Tariq
and Ayesha's Daughter
This
example demonstrates the
fact that each knowledge
representation scheme
has
its own strengths and
weaknesses.
4.5 Formal KR
techniques
In the
examples above, we explored
intuitive ways for knowledge
representation.
Now, we
will turn our attention to
formal KR techniques in AI. While
studying
these
techniques, it is important to remember
that each method is suited
to
representing a
certain type of knowledge.
Choosing the proper
representation is
93

Artificial
Intelligence (CS607)
important
because it must help in
reasoning. As the saying
goes `Knowledge is
Power'.
4.6
Facts
Facts are a
basic block of knowledge
(the atomic units of
knowledge). They
represent
declarative knowledge (they
declare knowledge about
objects). A
proposition
is
the statement of a fact.
Each proposition has an
associated truth
value. It may be
either true or false. In AI, to
represent a fact, we use
a
proposition and
its associated truth value,
e.g.
Proposition
A: It is raining
Proposition
B: I have an umbrella
Proposition
C: I will go to school
4.6.1 Types of
facts
Single-valued or
multiple valued
Facts may be
single-valued or multi-valued, where
each fact (attribute) can
take
one or more
than one values at the same
time, e.g. an individual can
only have
one eye
color, but may have many
cars. So the value of
attribute cars may
contain
more than one value.
Uncertain
facts
Sometimes we
need to represent uncertain
information in facts. These
facts are
called
uncertain facts, e.g. it
will probably be sunny
today. We may chose to
store
numerical
certainty values with
such facts that tell us
how much uncertainty
there
is in the
fact.
Fuzzy
facts
Fuzzy
facts are ambiguous
in
nature, e.g. the book is
heavy/light. Here it is
unclear
what heavy means because it
is a subjective description.
Fuzzy
representation is
used for such facts.
While defining fuzzy facts,
we use certainty
factor
values to specify value of
"truth". We will look at
fuzzy representation in
more
detail later.
Object-Attribute-Value
triplets
Object-Attribute
Value Triplets or OAV triplets
are a type of fact composed
of
three
parts; object, attribute and
value. Such facts are
used to assert a
particular
property of
some object, e.g.
Ali's eye
color is brown.
o Object:
Ali
o Attribute: eye
color
94
Artificial
Intelligence (CS607)
o Value:
brown
Ahmed's
son is Ali
o Object:
Ahmed
o Attribute:
son
o Value:
Ali
OAV Triplets
are also defined as in
figure below
Eye
Color
Ali
Brown
Object
Attribute
Value
Color
Ahmed
Red
Object
Attribute
Value
Figure: OAV
Triplets
4.7
Rules
Rules
are another form of
knowledge representation. Durkin
defines a rule as "A
knowledge
structure that relates some
known information to other
information
that
can be concluded or inferred to be
true."
4.7.1 Components
of a rule
A Rule
consists of two
components
o Antecedent or
premise or the IF
part
o Consequent or
conclusion or the THEN
part
For
example, we have a rule: IF it is
raining THEN I will not go to
school
Premise: It is
raining
Conclusion: I
will not go to
school.
4.7.2 Compound
Rules
Multiple
premises or antecedents may be joined
using AND (conjunctions) and
OR (disjunctions),
e.g.
IF it is raining
AND I have an umbrella
THEN I will go to
school.
IF it is raining
OR it is snowing
THEN I will
not go to school
95

Artificial
Intelligence (CS607)
4.7.3 Types of
rules
Relationship
Relationship
rules are used to express a
direct occurrence relationship
between
two
events, e.g. IF you hear a
loud sound THEN the silencer
is not working
Recommendation
Recommendation
rules offer a recommendation on
the basis of some
known
information,
e.g.
IF it is
raining
THEN bring an
umbrella
Directive
Directive
rules are like
recommendations rule but
they offer a specific line
of
action, as
opposed to the `advice' of a
recommendation rule,
e.g.
IF it is raining
AND you don't have an
umbrella
THEN wait
for the rain to
stop
Variable
Rules
If the
same type of rule is to be
applied to multiple objects, we
use variable rules,
i.e.
rules
with
variables,
e.g.
If
X
is
a
Student
AND
X's
GPA>3.7
THEN place X on
honor roll.
Such
rules are called
pattern-matching rules. The
rule is matched with
known
facts
and different possibilities
for the variables are
tested, to determine the
truth
of the
fact.
Uncertain
Rules
Uncertain
rules introduce uncertain
facts into the system,
e.g.
IF you
have never won a
match
THEN you
will most probably not
win this time.
Meta
Rules
Meta rules
describe how to use other
rules, e.g.
IF you
are coughing AND you have
chest congestion
THEN use
the set of respiratory
disease rules.
Rule
Sets
96
Artificial
Intelligence (CS607)
As in the
previous example, we may group
rules into categories in our
knowledge
representation
scheme, e.g. the set of
respiratory disease
rules
4.8
Semantic networks
Semantic
networks are graphs, with
nodes representing objects and
arcs
representing
relationships between objects.
Various types of relationships
may
be defined
using semantic networks. The
two most common types
of
relationships
are
IS-A (Inheritance
relation)
HAS (Ownership
relation)
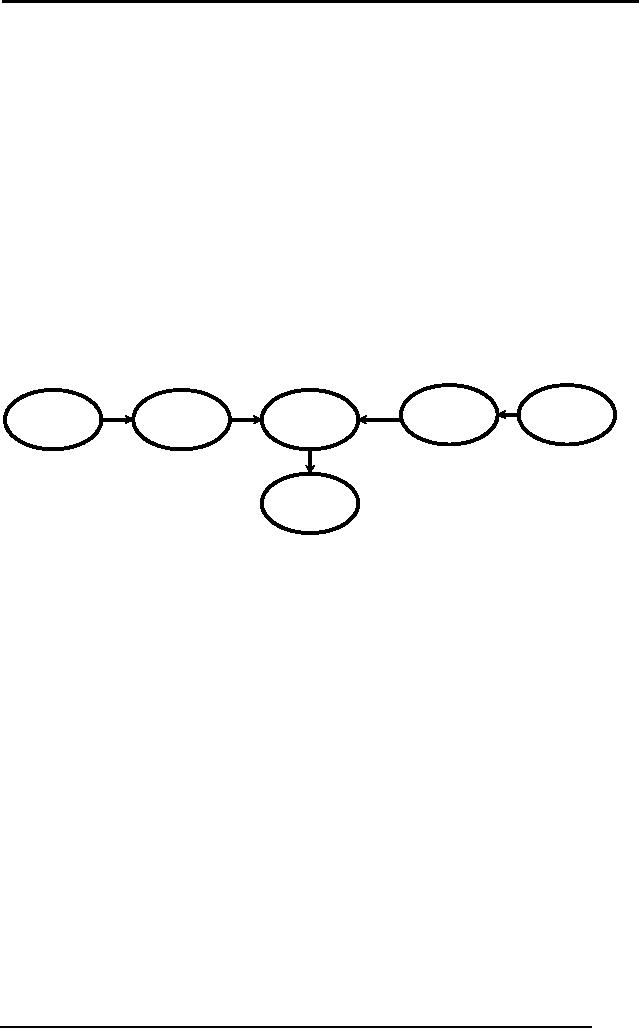
Let's
consider an example semantic
network to demonstrate how knowledge in
a
semantic
network can be used
IS-A
IS-A
IS-A
IS-A
Truck
Bedford
Suzuki
Car
Vehicle
Travels
by
Road
Figure:
Vehicle Semantic
Network
Network
Operation
To infer
new information from
semantic networks, we can
ask questions from
nodes
Ask node
vehicle: `How do you
travel?'
This
node looks at arc and
replies: road
Ask node
Suzuki: `How do you
travel?'
This
node does not have a
link to travel therefore it
asks other
nodes
linked by the IS-A
link
Asks
node Car (because of IS-A
relationship)
Asks
node Vehicle (IS-A
relationship)
Node Vehicle
Replies: road
Problems
with Semantic
Networks
o Semantic
networks are computationally
expensive at run-time as we
need
to traverse
the network to answer some
question. In the worst case,
we
may need to
traverse the entire network
and then discover that
the
requested
info does not
exist.
o They
try to model human
associative memory (store
information using
associations),
but in the human brain
the number of neurons and
links are
97

Artificial
Intelligence (CS607)
in the
order of 1015. It is
not practical to build such
a large semantic
network,
hence this scheme is not
feasible for this type of
problems.
o Semantic
networks are logically
inadequate as they do not
have any
equivalent
quantifiers, e.g., for all,
for some, none.
4.9
Frames
"Frames
are data structures for
representing stereotypical knowledge of
some
concept or
object" according to Durkin, a
frame is like a schema, as we
would call
it in a database
design. They were developed
from semantic networks and
later
evolved
into our modern-day Classes
and Objects. For example, to
represent a
student, we
make use of the following
frame:
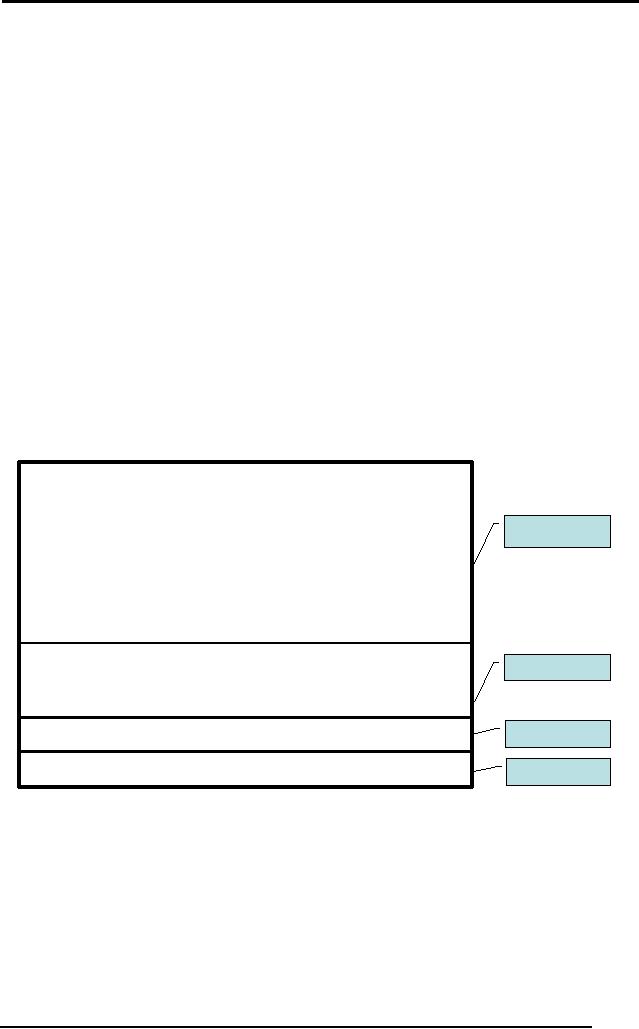
Frame
Name: Student
Properties:
Age: 19
GPA:
4.0
Ranking:
1
Figure:
Student Frame
The various
components within the frame
are called slots, e.g.
Frame Name slot.
4.9.1
Facets
A slot in a
frame can hold more
that just a value, it
consists of metadata and
procedures
also. The various aspects of a
slot are called facets.
They are a
feature of
frames that allows us to put
constraints on frames. e.g.
IF-NEEDED
Facets
are called when the
data of a particular slot is
needed. Similarly,
IF-
CHANGED Facets
are when the value of a
slot changes.
4.10
Logic
Just
like algebra is a type of
formal logic that deals
with numbers, e.g. 2+4 =
6,
propositional
logic and predicate calculus
are forms of formal logic
for dealing
with
propositions. We will consider
two basic logic
representation techniques:
Propositional
Logic
Predicate
Calculus
4.10.1
Propositional
logic
A proposition is
the statement of a fact. We
usually assign a symbolic
variable to
represent a
proposition, e.g.
98
Artificial
Intelligence (CS607)
p = It is
raining
q = I carry an
umbrella
A proposition is a
sentence whose truth values
may be determined. So,
each
proposition
has a truth value,
e.g.
The
proposition `A rectangle has
four sides' is true
The
proposition `The world is a
cube' is false.
4.10.1.1
Compound
statements
Different
propositions may be logically related and
we can form compound
statements
of propositions using
logical connectives.
Common logical
connectives
are:
AND
(Conjunction)
∧
OR
(Disjunction)
∨
NOT
(Negation)
¬
If ... then
(Conditional)
→
If and
only if (bi-conditional)
⇔
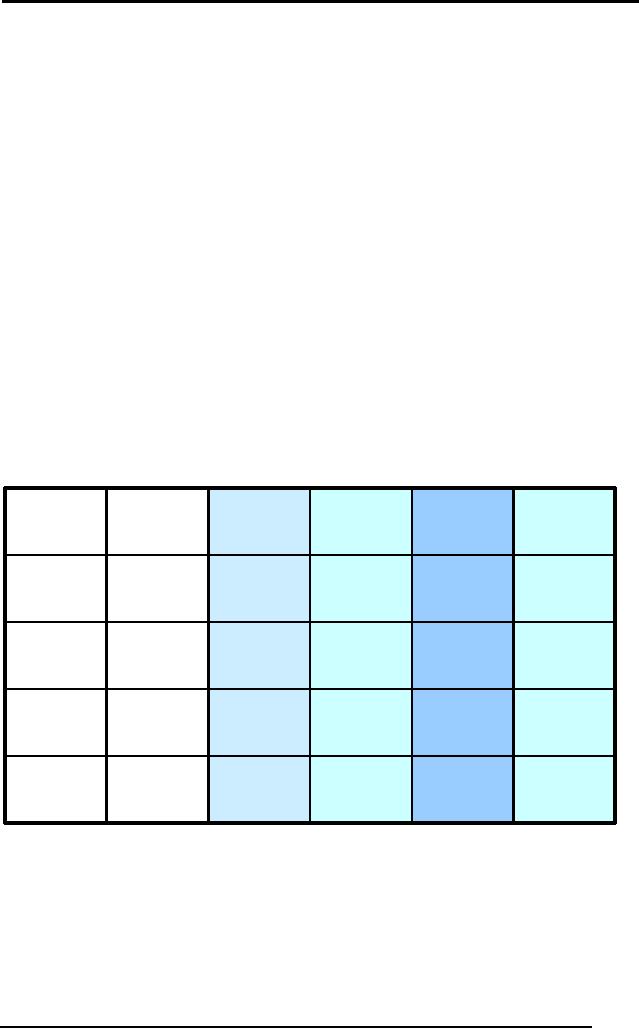
The table
below shows the logic of
the above connectives
p
q
p ∧q
p∨q
p⇒q
p⇔q
T
T
T
T
T
T
T
F
F
T
F
F
F
T
F
T
T
F
F
F
F
F
T
T
Figure:
Truth Table of Binary
Logical Connectives
4.10.1.2
Limitations
of propositional logic
o Propositions
can only represent knowledge
as complete sentences,
e.g.
a = the
ball's color is blue.
o Cannot
analyze the internal
structure of the
sentence.
99

Artificial
Intelligence (CS607)
o No quantifiers
are available, e.g. for-all,
there-exists
o Propositional
logic provides no framework
for proving statements such
as:
All
humans are mortal
All
women are humans
Therefore,
all women are
mortals
This is a
limitation in its representational
power.
4.10.2
Predicate
calculus
Predicate
Calculus is an extension of propositional
logic that allows the
structure
of facts
and sentences to be defined.
With predicate logic, we can
use
expressions
like
Color(
ball, blue)
This
allows the relationship of
sub-sentence units to be expressed,
e.g. the
relationship
between color, ball and blue
in the above example. Due to
its greater
representational
power, predicate calculus
provides a mechanism for
proving
statements and
can be used as a logic
system for proving logical
theorems.
4.10.2.1
Quantifiers
Predicate
calculus allows us to use
quantifiers for statements.
Quantifiers allow
us to say
things about some or all
objects within some set. The
logical quantifiers
used in
basic predicate calculus are
universal and existential
quantifiers.
The Universal
quantifier
The symbol
for the universal quantifier
is ∀
It is
read as "for every" or "for
all" and
used in
formulae to assign the same
truth value to all variables
in the domain,
e.g. in
the domain of numbers, we
can say that ( ∀ x) ( x + x = 2x).
In words this
is:
for every x (where x is a
number), x + x = 2x is true. Similarly,
in the domain of
shapes, we
can say that ( ∀ x) (x = square
→
x =
polygon), which is read
in
words
as: every square is a
polygon. In other words, for
every x (where x is a
shape), if x is a
square, then x is a polygon
(it implies that x is a
polygon).
Existential
quantifier
The symbol
for the existential
quantifier is ∃ . It is read as
"there exists", " for
some",
"for at least one", "there
is one", and is used in formulae to
say that
something is
true for at least one value
in the domain, e.g. in the
domain of
persons, we
can say that
( ∃ x) (Person
(x) ∧ father
(x, Ahmed) ). In words this
reads as: there exists
some
person, x
who is Ahmed's
father.
4.10.2.2
First
order predicate logic
100
Artificial
Intelligence (CS607)
First
order predicate logic is the
simplest form of predicate
logic. The main types
of symbols
used are
Constants
are used to name specific
objects or properties, e.g.
Ali, Ayesha,
blue,
ball.
Predicates: A
fact or proposition is divided
into two parts
Predicate:
the assertion of the
proposition
Argument:
the object of the
proposition
For
example, the proposition
"Ali likes bananas" can be
represented in predicate
logic as
Likes (Ali, bananas), where
Likes is the predicate and
Ali and bananas
are
the arguments.
Variables:
Variables are used to a
represent general class of
objects/properties,
e.g. in
the predicate likes (X,
Y), X and Y are variables
that assume the
values
X=Ali
and Y=bananas
Formulae:
Formulas
combine
predicates
and
quantifiers
to
represent
information
Lets us
illustrate these symbols
using an example
man(ahmed)
father(ahmed,
belal)
brother(ahmed,
chand)
Predicates
owns(belal,
car)
tall(belal)
hates(ahmed,
chand)
family()
∀ Y (¬sister(Y,ahmed))
Formulae
∀X,Y,Z(man(X)
∧
man(Y)
man(Z)
∧ father(Z,Y)
∧ father(Z,X)
⇒
brother(X,Y))
X, Y and Z
Variables
ahmed,
belal, chand and car
Constants
Figure :
Predicate Logic
Example
The predicate
section outlines the known
facts about the situation in
the form of
predicates,
i.e. predicate name and
its arguments. So,
man(ahmed) means that
ahmed is a
man, hates(ahmed, chand)
means that ahmed hates
chand.
101

Artificial
Intelligence (CS607)
The formulae
sections outlines formulae
that use universal
quantifiers and
variables to
define certain rules. ∀ Y (¬sister(Y,ahmed))
says that there
exists
no Y such
that Y is the sister of
ahmed, i.e. ahmed has no
sister. Similarly,
∀X,Y,Z(man(X)
∧
man(Y)
man(Z)
∧ father(Z,Y)
∧
father(Z,X)
⇒
brother(X,Y))
means
that if there are three
men, X, Y and Z, and Z is
the father of both X
and Y,
then X and Y are bothers.
This expresses the rule
for the two
individuals
being brothers.
4.11
Reasoning
Now that we
have looked at knowledge
representation, we will look
at
mechanisms to
reason on the knowledge once
we have represented it
using
some
logical scheme. Reasoning is
the process of deriving
logical conclusions
from
given facts. Durkin defines
reasoning as `the process of
working with
knowledge,
facts and problem solving
strategies to draw
conclusions'.
Throughout
this section, you will
notice how representing
knowledge in a
particular
way is useful for a
particular kind of
reasoning.
4.12
Types of reasoning
We will
look at some broad
categories of reasoning
4.12.1.1
Deductive
reasoning
Deductive
reasoning, as the name
implies, is based on deducing
new information
from
logically related known
information. A deductive argument
offers assertions
that
lead automatically to a conclusion,
e.g.
If there is
dry wood, oxygen and a
spark, there will be a
fire
Given:
There is dry wood, oxygen
and a spark
We can
deduce: There will be a
fire.
All men
are mortal. Socrates is a
man.
We can
deduce: Socrates is
mortal
4.12.2
Inductive
reasoning
Inductive
reasoning is based on forming, or
inducing a `generalization' from
a
limited
set of observations,
e.g.
Observation:
All the crows that I
have seen in my life are
black.
Conclusion:
All crows are
black
Comparison of
deductive and inductive
reasoning
We can
compare deductive and inductive
reasoning using an example.
We
conclude
what will happen when we
let a ball go using both
each type of
reasoning in
turn
102

Artificial
Intelligence (CS607)
The inductive
reasoning is as follows: By experience,
every time I have let a
ball
go, it
falls downwards. Therefore, I
conclude that the next
time I let a ball go,
it
will
also come down.
The deductive
reasoning is as follows: I know
Newton's Laws. So I
conclude
that if I
let a ball go, it will
certainly fall
downwards.
Thus
the essential difference is
that inductive reasoning is
based on experience
while
deductive reasoning is based on
rules, hence the latter
will always be
correct.
4.12.3
Abductive
reasoning
Deduction is
exact in the sense that
deductions follow in a logically
provable way
from
the axioms. Abduction is a
form of deduction that
allows for plausible
inference,
i.e. the conclusion might be
wrong, e.g.
Implication: She
carries an umbrella if it is
raining
Axiom:
she is carrying an
umbrella
Conclusion: It is
raining
This
conclusion might be false,
because there could be other
reasons that she is
carrying an
umbrella, e.g. she might be
carrying it to protect herself
from the sun.
4.12.4
Analogical
reasoning
Analogical
reasoning works by drawing
analogies between two
situations, looking
for
similarities and differences, e.g.
when you say driving a truck
is just like
driving a
car, by analogy you know
that there are some
similarities in the
driving
mechanism,
but you also know that
there are certain other
distinct characteristics
of
each.
4.12.5
Common-sense
reasoning
Common-sense
reasoning is an informal form of
reasoning that uses rules
gained
through
experience or what we call
rules-of-thumb. It operates on
heuristic
knowledge
and heuristic rules.
4.12.6
Non-Monotonic
reasoning
Non-Monotonic
reasoning is used when the
facts of the case are
likely to change
after
some time, e.g.
Rule:
IF the
wind blows
THEN the
curtains sway
When
the wind stops blowing,
the curtains should sway no
longer. However, if we
use
monotonic reasoning, this
would not happen. The fact
that the curtains
are
swaying
would be retained even after
the wind stopped blowing. In
non-
103

Artificial
Intelligence (CS607)
monotonic
reasoning, we have a `truth
maintenance system'. It keeps
track of
what
caused a fact to become
true. If the cause is
removed, that fact is
removed
(retracted)
also.
4.12.7
Inference
Inference is
the process of deriving new
information from known
information. In
the
domain of AI, the component of
the system that performs
inference is called
an inference
engine. We will
look at inference within the
framework of `logic',
which we
introduced earlier
4.12.7.1
Logic
Logic,
which we introduced earlier,
can be viewed as a formal
language. As a
language, it
has the following
components: syntax, semantics and
proof systems.
Syntax
Syntax is a
description of valid statements,
the expressions that are
legal in that
language. We
have already looked at the
syntax of two type of logic
systems
called
propositional logic and
predicate logic. The syntax
of proposition gives us
ways to
use propositions, their
associated truth value and
logical connectives to
reason.
Semantics
Semantics
pertain to what expressions
mean, e.g. the expression
`the cat drove
the
car' is syntactically correct,
but semantically
non-sensible.
Proof
systems
A logic
framework comes with a proof
system, which is a way of
manipulating
given
statements to arrive at new statements.
The idea is to derive
`new'
information
from the given
information.
Recall
proofs in math class. You
write down all you know
about the situation
and
then
try to apply all the
rules you know repeatedly
until you come up with
the
statement you
were supposed to prove.
Formally, a proof is a sequence
of
statements
aiming at inferring some
information. While doing a
proof, you usually
proceed
with the following
steps:
You begin
with initial statements,
called premises of the proof
(or knowledge
base)
Use rules,
i.e. apply rules to the
known information
Add new
statements, based on the
rules that match
Repeat
the above steps until you
arrive at the statement you
wished to prove.
4.12.7.1.1
Rules of
inference
104
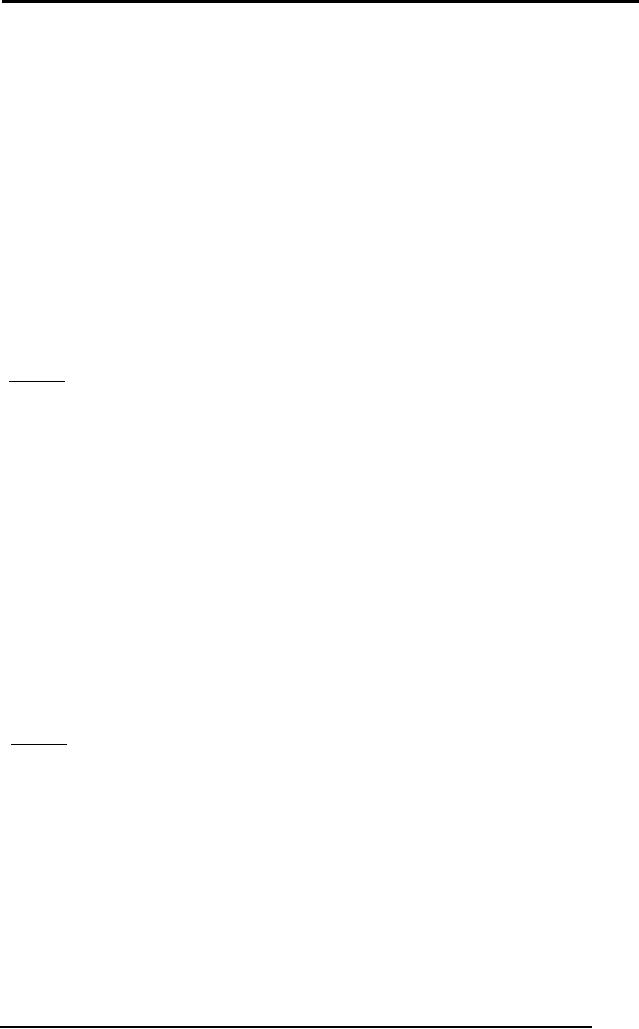
Artificial
Intelligence (CS607)
Rules of
inference are logical rules
that you can use to prove
certain things. As
you look at
the rules of inference, try
to figure out and convince
yourself that the
rules
are logically sound, by
looking at the associated
truth tables. The rules
we
will
use for propositional logic
are:
Modus
Ponens
Modus
Tolens
And-Introduction
And-Elimination
Modus
ponens
"Modus
ponens" means "affirming
method". Note: From now on
in our discussion
of logic,
anything that is written
down in a proof is a statement
that is true.
α →β
α
β
Modus-
Ponens
Modus
Ponens says that if you
know that alpha implies
beta, and you know
alpha
to be true,
you can automatically say
that beta is true.
Modus
Tolens
Modus
Tolens says that "alpha
implies beta" and "not
beta" you can
conclude
"not
alpha". In other words, if
Alpha implies beta is true
and beta is known to be
not
true, then alpha could
not have been true. Had
alpha been true, beta
would
automatically
have been true due to the
implication.
α →β
¬β
¬α
Modus -
Tolens
And-Introduction and
and-Elimination
And-introduction
say that from "Alpha" and
from "Beta" you can conclude
"Alpha
and Beta".
That seems pretty obvious,
but is a useful tool to know
upfront.
Conversely,
and-elimination says that
from "Alpha and Beta" you
can conclude
"Alpha".
105
Artificial
Intelligence (CS607)
α
α ∧β
β
α
α ∧β
And-
And-
elimination
Introduction
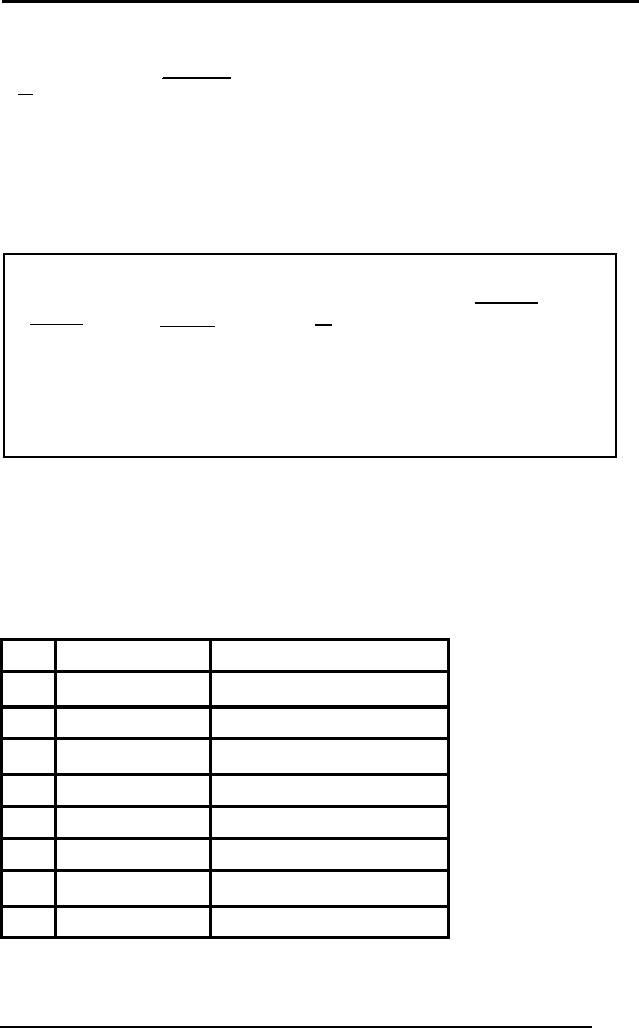
The table
below gives the four
rules of inference
together:
α
α ∧β
α →β
α →β
β
α
¬β
α
β
¬α
α ∧β
And-
Modus
And-
Modus
elimination
Ponens
Introduction
Tolens
Figure :
Table of Rules of
Inference
4.12.7.2
Inference
example
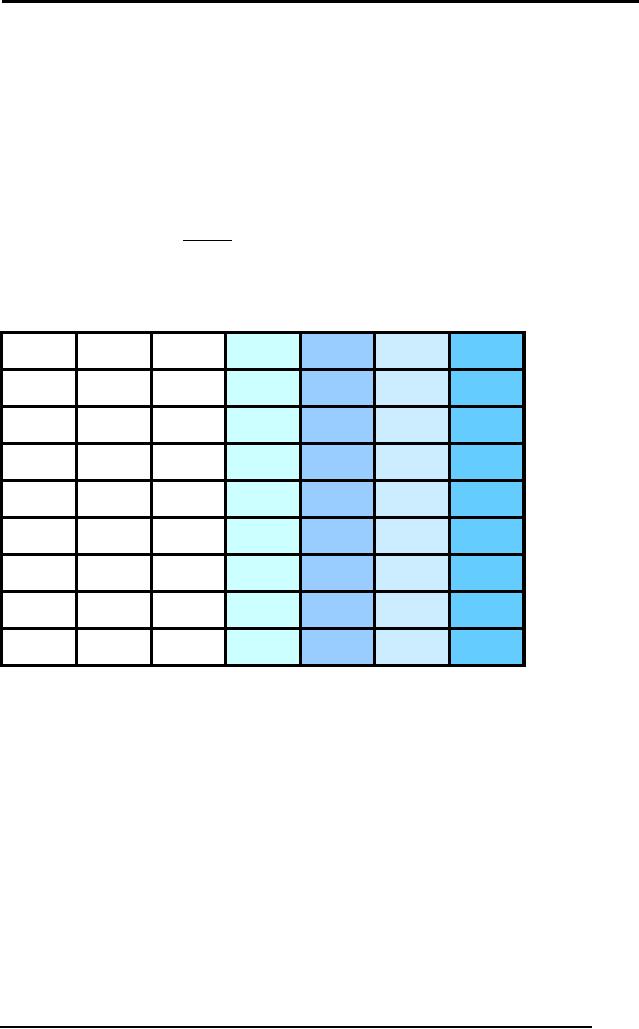
Now, we
will do an example using the
above rules. Steps 1, 2 and
3 are added
initially,
they are the given
facts. The goal is to prove
D. Steps 4-8 use the
rules
of inference to
reach at the required goal
from the given
rules.
Step
Formula
Derivation
1
Given
A∧B
2
A→C
Given
3
Given
(B ∧ C) →D
4
A
1
And-elimination
5
C
4, 2 Modus
Ponens
6
B
1
And-elimination
5, 6
And-introduction
7
B ∧C
8
D
7, 3 Modus
Ponens
Note: The
numbers in the derivation
reference the statements of
other step
numbers.
106
Artificial
Intelligence (CS607)
4.12.7.3
Resolution
rule
The deduction
mechanism we discussed above,
using the four rules of
inference
may be used in
practical systems, but is
not feasible. It uses a lot
of inference
rules
that introduce a large
branch factor in the search
for a proof. An
alternative
is approach is
called resolution, a strategy
used to determine the truth
of an
assertion,
using only one resolution
rule:
α∨β
¬β ∨ γ
α ∨γ
To see
how this rule is logically
correct, look at the table
below:
Α
β
Γ
¬β
α ∨γ
α∨β
¬β ∨ γ
F
F
F
T
F
T
F
F
F
T
T
F
T
T
F
T
F
F
T
F
F
F
T
T
F
T
T
T
T
F
F
T
T
T
T
T
F
T
T
T
T
T
T
T
F
F
T
F
T
T
T
T
F
T
T
T
You can
see that the rows
where the premises of the
rule are true, the
conclusion
of the
rule is true also.
To be able to
use the resolution rule
for proofs, the first
step is to convert all
given
statements
into the conjunctive normal
form.
4.12.7.4
Conjunctive
normal form
Resolution
requires all sentences to be
converted into a special
form called
conjunctive
normal form (CNF). A
statement in conjunctive normal
form (CNF)
consists of
ANDs of Ors. A sentence
written in CNF looks
like
( A ∨ B) ∧ (B ∨ ¬C ) ∧ (D)
note
:
D
=
(
D
∨
¬D)
107

Artificial
Intelligence (CS607)
The outermost
structure is made up of conjunctions.
Inner units called
clauses
are
made up of disjunctions. The components
of a statement in CNF are
clauses
and literals. A
clause is the disjunction of
many units. The units that
make up a
clause
are called literals. And a
literal is either a variable or
the negation of a
variable. So you
get an expression where the
negations are pushed in as
tightly
as possible,
then you have ORs, then
you have ANDs. You can
think of each
clause as a
requirement. Each clause has
to be satisfied individually to satisfy
the
entire
statement.
4.12.7.5
Conversion
to CNF
1. Eliminate
arrows (implications)
A → B = ¬A ∨ B
2. Drive in
negations using De Morgan's
Laws, which are given
below
¬( A ∨ B) = (¬A ∧ ¬B)
¬( A ∧ B) = (¬A ∨ ¬B)
3. Distribute OR
over AND
A ∨ (B ∧ C)
= ( A ∨ B) ∧ ( A ∨ C )
4.12.7.6
Example
of CNF conversion
( A ∨ B ) → (C → D )
1.¬( A ∨ B ) ∨ (¬C ∨ D )
2.(¬A ∧ ¬B ) ∨ (¬C ∨ D )
3.(¬A ∨ ¬C ∨ D ) ∧ (¬B ∨ ¬C ∨ D )
4.12.7.7
Resolution
by Refutation
Now, we
will look at a proof
strategy called resolution
refutation. The steps
for
proving a
statement using resolution
refutation are:
· Write
all sentences in CNF
· Negate
the desired
conclusion
· Apply
the resolution rule until
you derive a contradiction or cannot
apply
the
rule anymore.
· If we derive
a contradiction, then the
conclusion follows from the
given
axioms
· If we cannot
apply anymore, then the
conclusion cannot be proved
from
the
given axioms
108
Artificial
Intelligence (CS607)
4.12.8
Resolution refutation example
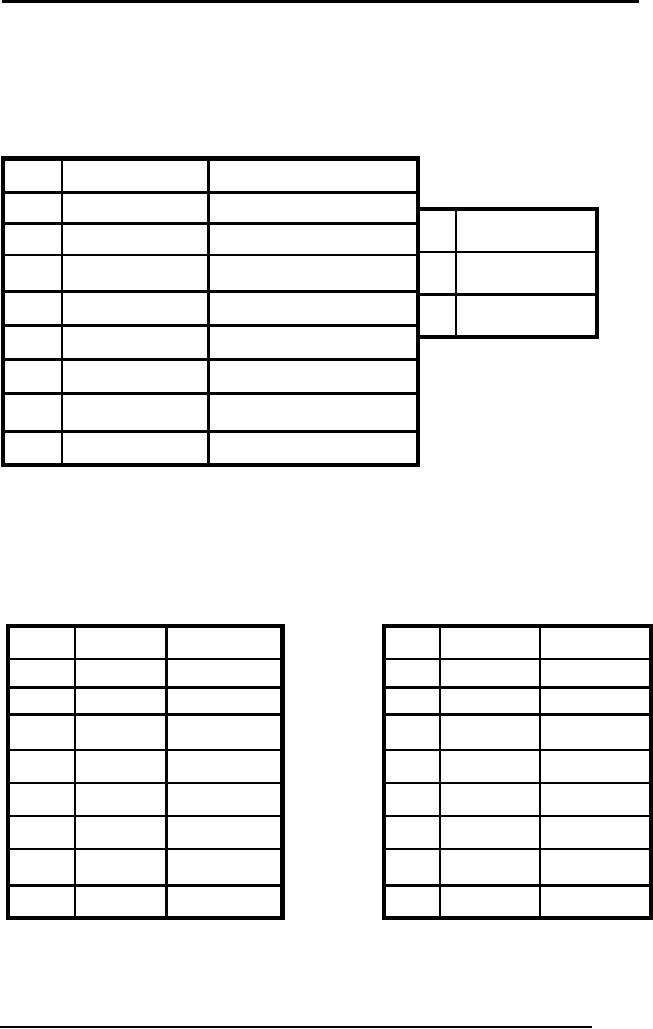
1
Prove
C
Ste
Formula
Derivation
p
1
Given
A∨B
1
A∨B
2
Given
¬A ∨ C
2
A→C
3
Given
¬B ∨ C
4
¬C
Negated
Conclusion
3
B →C
1, 2
5
B∨C
6
¬A
2, 4
7
¬B
3, 4
8
C
5, 7
Contradiction!
The statements in
the table on the right
are the given statements.
These are
converted to CNF
and are included as steps 1, 2
and 3. Our goal is to prove
C.
Step 4 is
the addition of the negation
of the desired conclusion.
Steps 5-8 use
the
resolution
rule to prove C.
Note
that you could have come up
with multiple ways of
proving R:
Step
Formula
Step
Formula
1
Given
1
Given
A∨B
A∨B
2
Given
2
Given
¬A ∨ C
¬A ∨ C
3
Given
3
Given
¬B ∨ C
¬B ∨ C
4
¬C
4
¬C
5
¬B
3,4
1,2
5
B∨C
6
A
1,5
6
¬A
2,4
7
2,6
7
¬B
3,4
C
8
5,7
C
4.12.9
Resolution Refutation Example
2
109
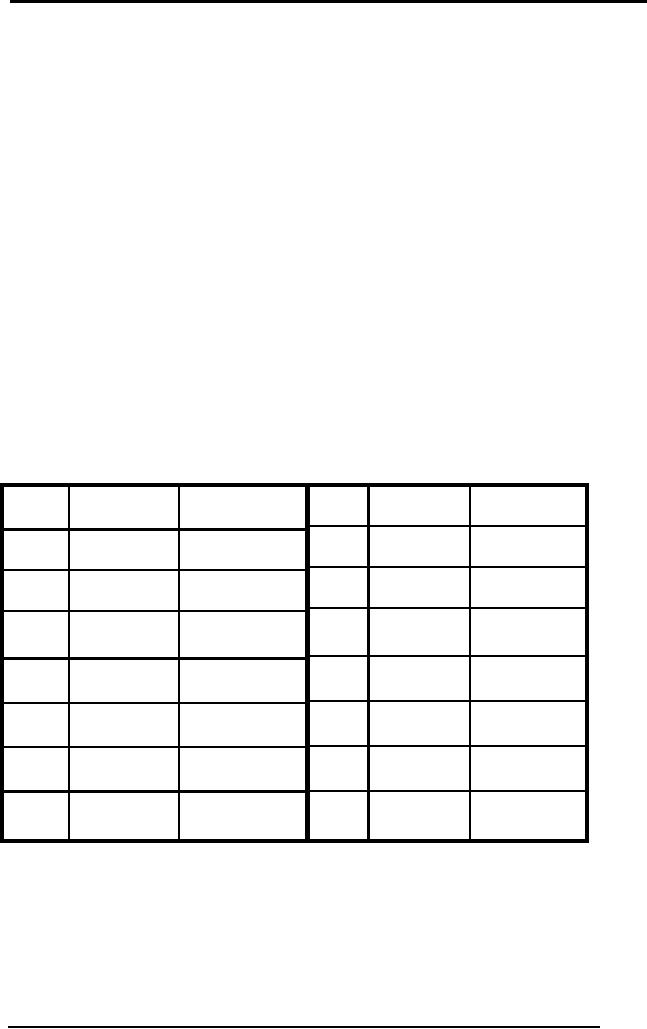
Artificial
Intelligence (CS607)
1. (A→B) →B
2. A→C
3. ¬C → ¬B
Prove
C
Convert to
CNF
1.( A → B) → B
= (¬A ∨ B) → B
= ¬(¬A ∨ B) ∨ B
= ( A ∧ ¬B) ∨ B
= ( A ∨ B) ∧ (¬B ∨ B)
= ( A ∨ B)
2. A → C = ¬A ∨ C
3.¬C → ¬B = C ∨ ¬B
Proof
Step
Formula
Derivation
Step
Formula
Derivation
1
Given
B∨A
1
Given
B∨A
2
Given
¬A∨C
Given
2
¬A∨C
3
Given
C ∨ ¬B
3
Given
C ∨ ¬B
4
¬C
Negation
of
Negation
of
4
¬C
conclusion
conclusion
5
¬B
3,4
5
A
2,4
6
A
1,5
6
C
2,5
7
C
2,6
4.12.9.1
Proof
strategies
As you
can see from the
examples above, it is often
possible to apply
more
than one
rule at a particular step. We
can use several strategies
in such
cases. We
may apply rules in an
arbitrary order, but there
are some rules of
thumb
that may make the search
more efficient
110