Finite Automaton with output, Moore machine

<< Distinguishable strings and Indistinguishable strings

Mealy machine >>

Theory of Automata

(CS402)

Theory of Automata

Lecture N0. 20

Reading Material

Introduction to Computer Theory

Chapter 8

Summary

Example of previous Theorem, Finite Automaton with output, Moore machine, Examples

Example

Let L20={w OE {0,1}*: |w| ≥ 20 and the 20th letter of w, from right is, 1}. Let S be the set of all strings of length

20, defined over Σ, any two of which are distinguishable w.r.t. L20. Obviously the number of strings belonging

to S, is 220. Let x and y be any two distinct strings i.e. they differ in ith letter, i=1,2,3,...20, from left. For i=1,

they differ by first letter from left.

Then by definition of L20, one is in L20 while other is not as shown below

...

So they are distinct w.r.t. L20 for z = L i.e. one of xz and yz belongs to L20.

Similarly if i=2 they differ by 2nd letter from left and are again distinguishable and hence for z belonging to Σ*,

|z|=1, either xz or yz belongs to L20 because in this case the 20th letter from the right of xz and yz is exactly the

2nd letter from left of x and y as shown below

...

Hence x and y will be distinguishable w.r.t. L20 for i=2, as well. Continuing the process it can be shown that any

pair of strings x and y belonging to S, will be distinguishable w.r.t. L20. Since S contains 220 strings, any two of

which are distinguishable w.r.t. L20, so using the theorem any FA accepting L20 must have at least 220 states.

Note

It may be observed from the above example that using Martin's method, there exists an FA having

220+1-1=2,097,151 states. This indicates the memory required to recognize L20 will be the memory of a computer

that can accommodate 21-bits i.e.the computer can be in 221 possible states.

Finite Automaton with output

Finite automaton discussed so far, is just associated with the RE or the language.

There is a question whether does there exist an FA which generates an output string corresponding to each input

string ? The answer is yes. Such machines are called machines with output.

There are two types of machines with output. Moore machine and Mealy machine

Moore machine

A Moore machine consists of the following

A finite set of states q0, q1, q2, ... where q0 is the initial state.

An alphabet of letters Σ = {a,b,c,...} from which the input strings are formed.

An alphabet G={x,y,z,...} of output characters from which output strings are generated.

A transition table that shows for each state and each input letter what state is entered the next.

An output table that shows what character is printed by each state as it is entered.

Note

It is to be noted that since in Moore machine no state is designated to be a final state, so there is no question of

accepting any language by Moore machine. However in some cases the relation between an input string and the

corresponding output string may be identified by the Moore machine. Moreover, the state to be initial is not

important as if the machine is used several times and is restarted after some time, the machine will be started

from the state where it was left off. Following are the examples

Theory of Automata

(CS402)

Example

Consider the following Moore machine having the states q0, q1, q2, q3 where q0 is the start state and

Σ = {a,b},

G={0,1}

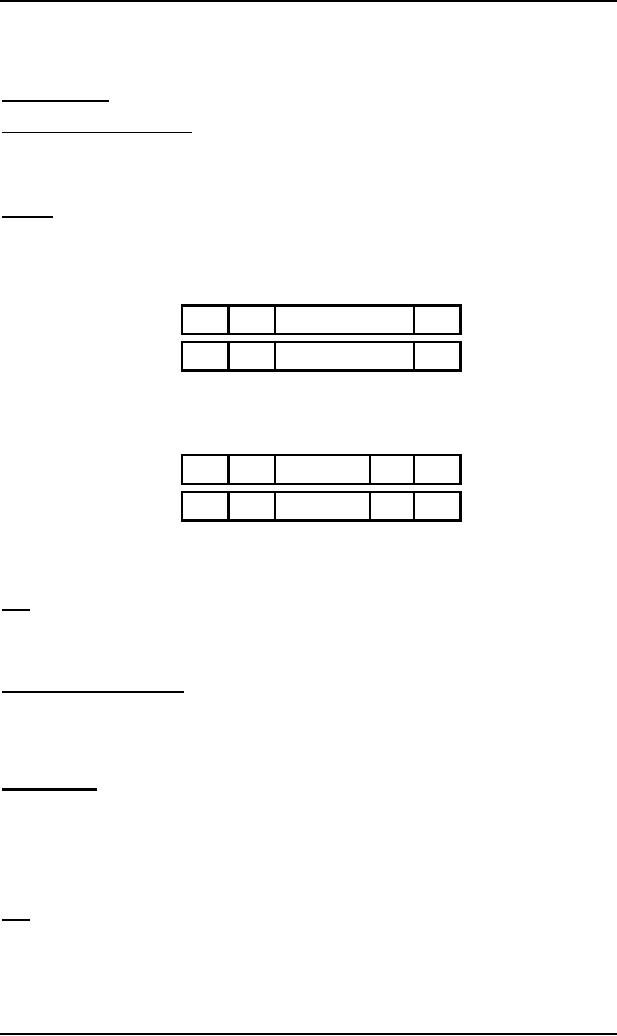
the transition table follows as

New States after reading

Characters

Old States

to be printed

q0-

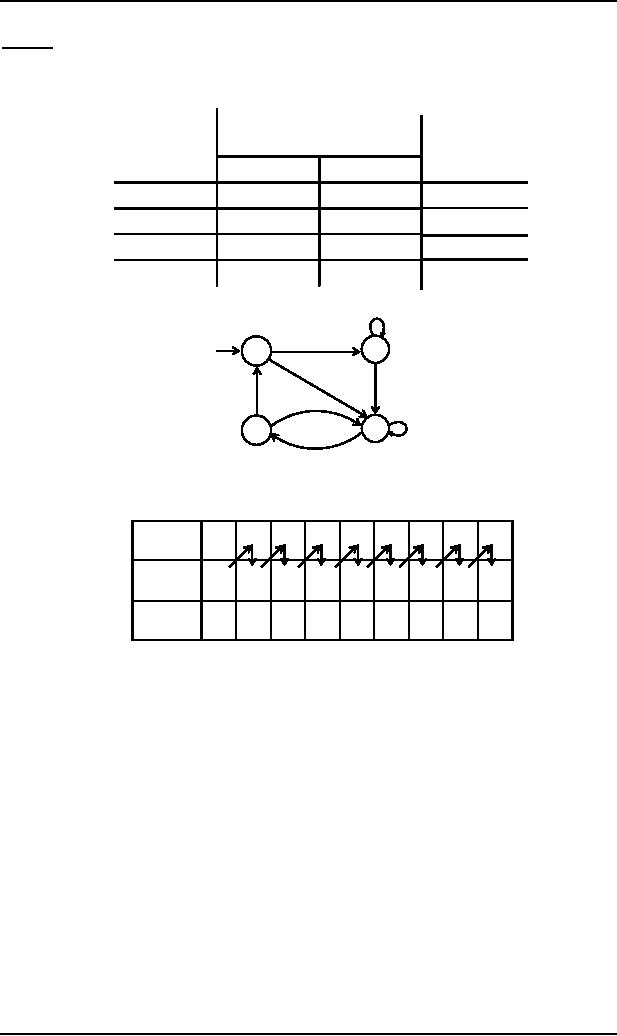
the transition diagram corresponding to the previous transition table may be

q1/0

q0/1

q3/1

q2/0

It is to be noted that the states are labeled along with the characters to be printed. Running the string abbabbba

over the above machine, the corresponding output string will be 100010101, which can be determined by the

following table as well

Input

State

output

It may be noted that the length of output string is l more than that of input string as the initial state prints out the

extra character 1, before the input string is read.

Table of Contents: