 |
Equivalent machines |
| << Mealy machine |
| Mealy machines in terms of sequential circuit >> |

Theory of
Automata
(CS402)
Theory of
Automata
Lecture
N0. 22
Reading
Material
Introduction
to Computer Theory
Chapter
8
Summary
Applications of
complementing and incrementing machines,
Equivalent machines, Moore
equivalent to Mealy,
proof,
example, Mealy equivalent to
Moore, proof, example
Applications
of Incrementing and Complementing
machines
1's
complementing and incrementing machines
which are basically Mealy
machines are very much
helpful in
computing.
The
incrementing machine helps in building a
machine that can perform
the addition of binary
numbers.
Using
the complementing machine along
with incrementing machine, one
can build a machine that
can perform
the
subtraction of binary numbers, as shown
in the following
method
Subtracting
a binary number from
another
Method
To
subtract a binary number b from a
binary number a
Add
1's complement of b to a (ignoring
the overflow, if any)
Increase
the result, in magnitude, by 1 (use
the incrementing machine ). Ignoring
the overflow if any.
Note:
If
there is no overflow in (1). Take
1's complement once again in
(2), instead. This situation
occurs when
b is
greater than a, in magnitude. Following
is an example of subtraction of binary
numbers
Example
To
subtract the binary number 101
from the binary number 1110,
let
a =
1110
and
b = 101 =
0101.
(Here
the number of digits of b are equated
with that of a)
Adding
1's complement (1010) of b to
a.
1110
+1010
11000
which gives 1000 (ignoring
the overflow)
Using
the incrementing machine, increase
the above result 1000, in
magnitude, by 1
1000
+1
1001
which is the same as obtained by
ordinary subtraction.
Note
It may be
noted that the above
method of subtraction of binary
numbers may be applied to subtraction
of
decimal
numbers with the change
that 9's complement of b
will be added to a, instead in
step (1).
Equivalent
machines
Two
machines are said to be equivalent
if
they print the same output
string when the same input
string is run on
them.
Remark:
Two
Moore machines may be
equivalent. Similarly two
Mealy machines may also be
equivalent, but a Moore
machine
can't be equivalent to any
Mealy machine. However,
ignoring the extra character
printed by the Moore
machine,
there exists a Mealy machine
which is equivalent to the
Moore machine.
Theorem
Statement
For
every Moore machine there is
a Mealy machine that is
equivalent to it (ignoring the
extra character
printed
by the
Moore machine).
Proof:
Let M be
a Moore machine, then
shifting the output characters
corresponding to each state to the
labels of
corresponding
incoming transitions, machine
thus obtained will be a Mealy
machine equivalent to M.
65
Theory of
Automata
(CS402)
Note
It may be
noted that while converting
a Moore machine into an
equivalent Mealy machine,
the output character
of a
state will be ignored if
there is no incoming transition at that
state. A loop at a state is
also supposed to be
an
incoming transition.
Following
is the example of converting a
Moore machine into an
equivalent Mealy
machine
Example
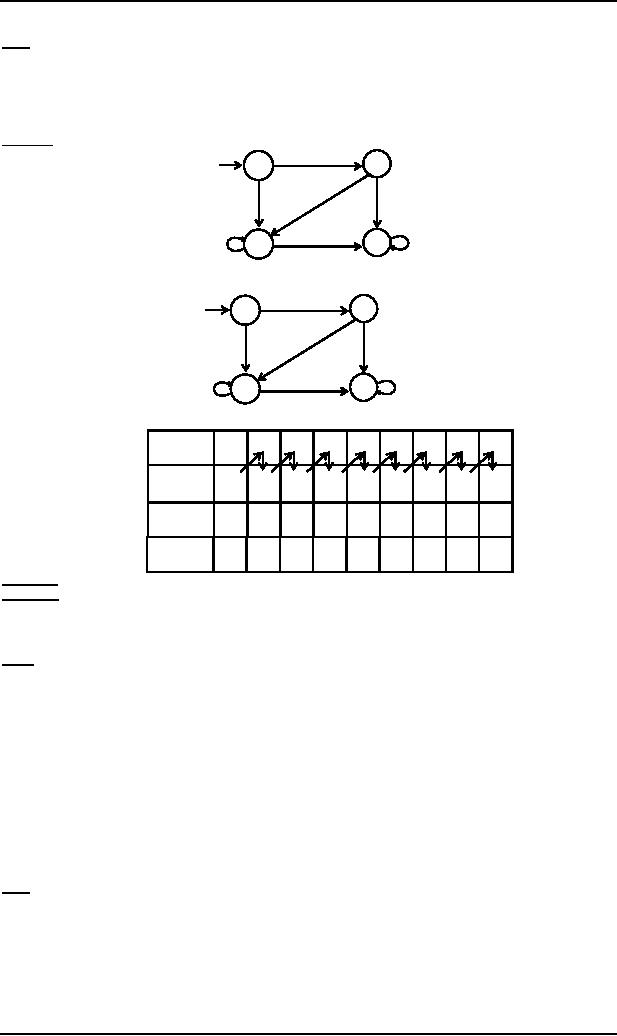
Consider
the following Moore
machine
a
q1/1
q0/0
b
a
b
b
q3/1
a,b
a
q2/0
Using
the method described
earlier, the above machine
may be equivalent to the
following Mealy
machine
a/1
q1
q
0
b/0
a/1
b/0
b/1
q3
q2
a/1,b/1
a/0
Running
the string abbabbba on both the
machines, the output string can be
determined by the following
table
a
b
b
a
b
b
b
a
Input
States
q3
q0
q1
q2
q3
q3
q3
q3
q3
Moore
0
1
0
1
1
1
1
1
1
Mealy
1
0
1
1
1
1
1
1
Theorem
Statement
For
every Mealy machine there is
a Moore machine that is
equivalent to it (ignoring the
extra character
printed
the
Moore machine).
Proof
Let M be
a Mealy machine. At each
state there are two
possibilities for incoming
transitions
The
incoming transitions have
the same output
character.
The
incoming transitions have
different output characters.
If all
the transitions have same
output characters, then shift
that character to the corresponding
state.
If all
the transitions have
different output characters, then
the state will be converted
to as many states as
the
number of
different output characters for
these transitions, which
shows that if this happens
at state qi
then
qi
will be
converted to qi1
and qi2 i.e.
if at
qi there are
the transitions with two
output characters then qi1 for one
character
and qi2
for other
character.
Shift
the output characters of the
transitions to the corresponding new
states qi1
and qi2. Moreover, these
new
states
qi1 and qi2 should behave like qi as well. Continuing the
process, the machine thus
obtained, will be a
Moore
machine equivalent to Mealy
machine M.
Following
is a note
Note
It may be
noted that if there is no
incoming transition at certain state then
any of the output characters
may be
associated
with that state.
It may
also be noted that if the
initial state is converted
into more than one new
states then only one of
these new
states
will be considered to be the
initial state. Following is an
example
66
Theory of
Automata
(CS402)
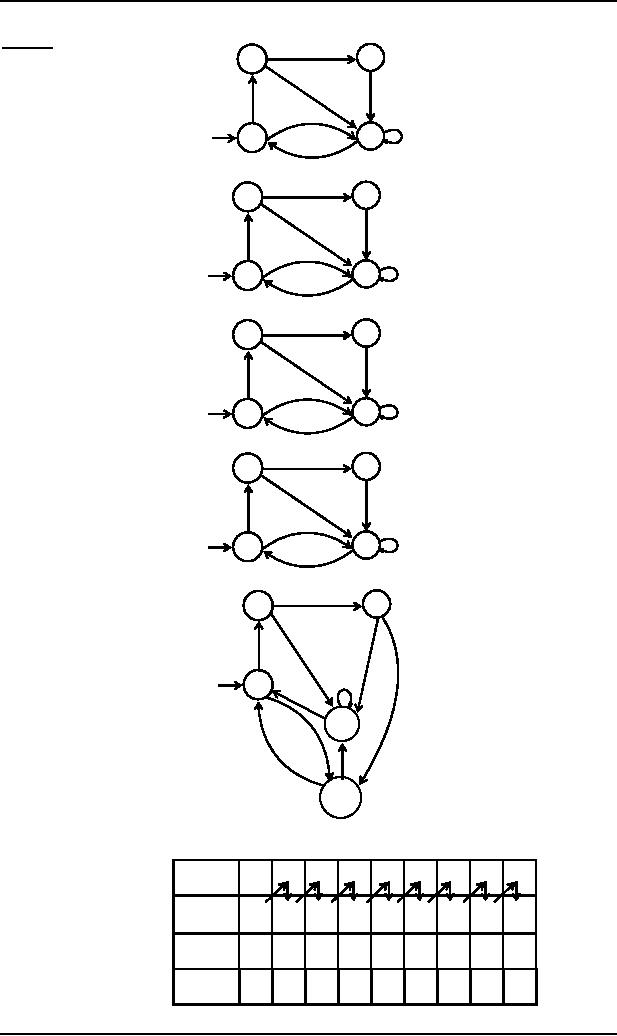
Example
b/1
q2
q1
Consider
the following Mealy
machine
b/1
a/0
a/0
a/1
q3
b/0
q0
a/1
b/1
Shifting
the output character 1 of transition b to q0
b/1
q2
q1
b/1
a/0
a/0
a/1
q3
b/0
a/1
q0/1
b
Shifting
the output character 0 of transition a to q1
b/1
q2
q1/0
b/1
a/0
a
a/1
q3
b/0
a/1
q0/1
b
Shifting
the output character 1 of transition b to q2
b
q2/1
q1/0
b/1
a/0
a
a/1
q3
b/0
a/1
q0/1
b
Splitting
q3
into
q13 and
q23
b
q2/1
q1/0
a
b
a
a
q0/1
b
a
1
q3/1
b
b
a
2
q3/0
Running
the string abbabbba on both the
machines, the output strings
can be determined by the following
table
b
b
b
a
Input
a
b
b
a
States
q0
q1
q2
q3
q3
q0
q3
q0
q1
Mealy
0
1
1
1
1
0
1
0
Moore
1
0
1
1
1
1
0
1
0
67
Table of Contents:
- What does automata mean, Introduction to languages
- Kleene Star Closure, Recursive definition of languages
- Regular Expression, Recursive definition of Regular Expression
- Equivalent Regular Expressions
- Finite Automaton
- Equivalent FAs
- FA corresponding to finite languages
- Examples of TGs: accepting all strings
- Generalized Transition Graphs
- Nondeterminism, Kleene’s Theorem
- Proof(Kleene’s Theorem Part II)
- Kleene’s Theorem Part III
- Concatenation of FAs
- Closure of an FA
- Nondeterministic Finite Automaton, Converting an FA to an equivalent NFA
- NFA with Null String
- NFA and Kleene’s Theorem
- NFA corresponding to Concatenation of FAs
- Distinguishable strings and Indistinguishable strings
- Finite Automaton with output, Moore machine
- Mealy machine
- Equivalent machines
- Mealy machines in terms of sequential circuit
- Regular languages, Complement of a language
- Nonregular languages
- Pumping Lemma
- Pumping Lemma version II
- Pseudo theorem
- Decidability
- finiteness of a language
- Context Free Grammar (CFG), CFG terminologies
- Trees
- Polish Notation (o-o-o)
- Total language tree, Regular Grammar
- Null Production
- Chomsky Normal Form (CNF)
- A new format for FAs
- Nondeterministic PDA
- PDA corresponding to CFG
- Conversion form of PDA
- Conversion Form, Joints of the machine
- Row language, Nonterminals
- Non-Context-Free language, Pumping lemma for CFLs
- Decidablity, Parsing Techniques
- Turing machine