Distinguishable strings and Indistinguishable strings

<< NFA corresponding to Concatenation of FAs

Finite Automaton with output, Moore machine >>

Theory of Automata

(CS402)

Theory of Automata

Lecture N0. 19

Reading Material

Introduction to Computer Theory

Chapter 7

Summary

NFA corresponding to Closure of FA, Examples, Memory required to recognize a language, Example,

Distinguishing one string from another, Example, Theorem, Proof

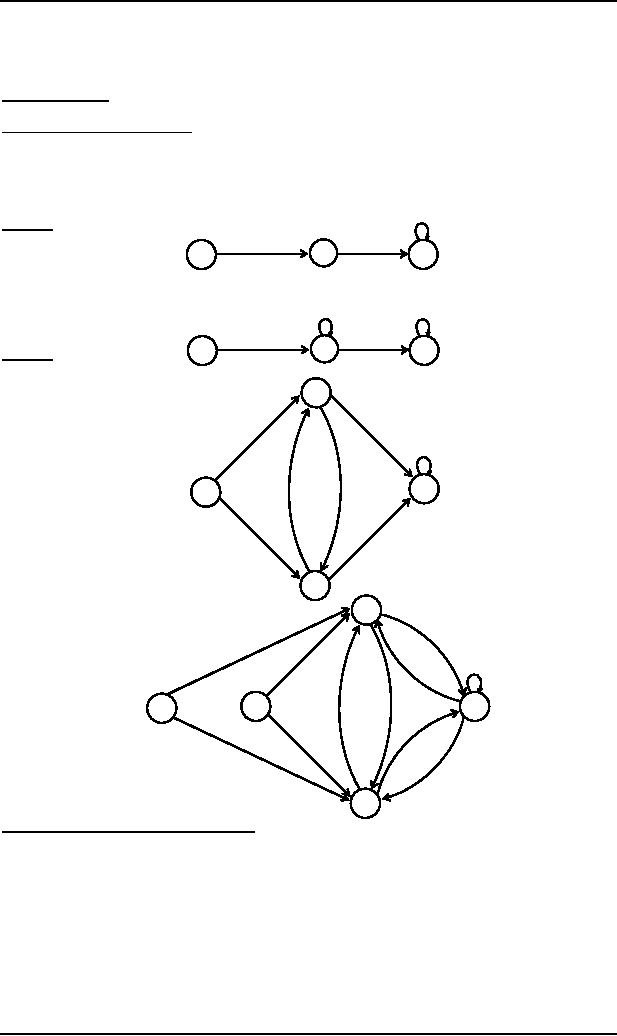
a,b

Example

Consider the following FA

a, b

1±

It can be observed that FA*not only accepts the Null string but every other string as well.

Here we don't need separate initial and final state. Hence an NFA corresponding to FA* may be

a,b

a, b

1±

Example

Consider the following FA

0,1

The NFA corresponding to FA* may be as follows

0,1

Memory required to recognize a language

Memory required to recognize a language means to look at the machine which can recognize a language. As an

FA can be considered to be a machine which is simple model of computation and every regular language is

associated with certain FA, so to recognize a language there is a restriction that there is a single pass from left to

right for any string to decide whether it belongs to certain language ? This helps to remember the information

about the initial part of the string read so far.

By this process the input string is examined and the string is decided either to be in a certain language or not.

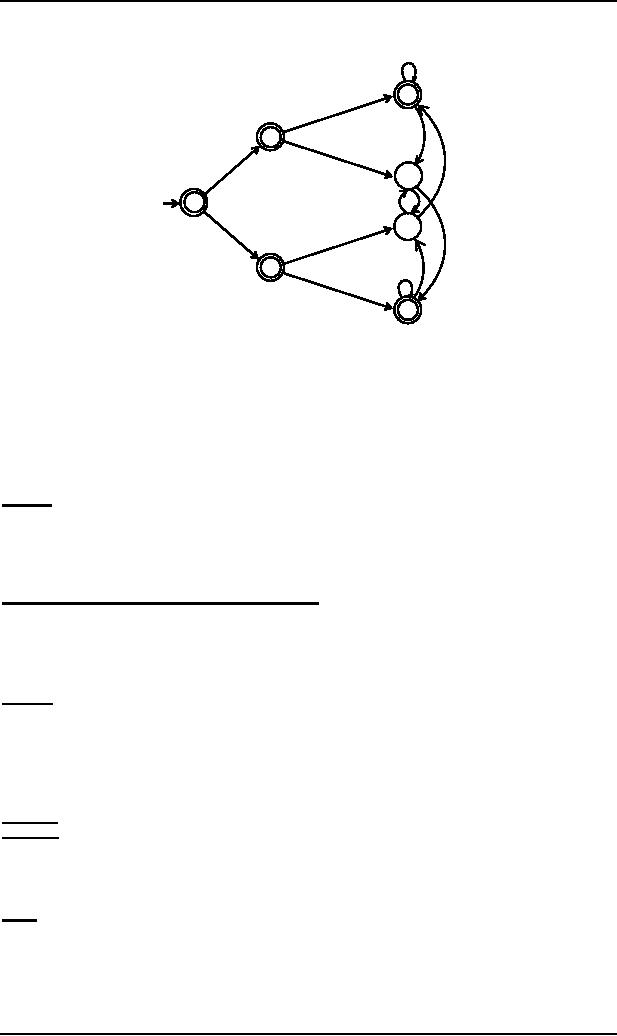
Consider L = {w OE {a,b}*: w neither ends in ab nor in ba}. i.e. L is the language of strings, defined over Σ =

{a,b}, consisting of Λ, a, b and strings ending in aa or bb. L may be accepted by the following FA

Theory of Automata

(CS402)

As seen in the above FA, seven states are required to recognize the language L, while on the other hand it is

very hard to recognize the language PALINDROME.

As seen in the above example of FA, seven states are required to recognize that language. Now consider another

language L3 of strings of length three or more, defined over Σ = {a,b}, and the third letter from the right is a.

As discussed by Martin, there is a straight forward method to build an FA recognizing L3 i.e. a distinct state for

every possible substring of length less then or equal to 3. It is obvious that for each length i, i=0,1,2,3, of

substring, the number of states are 2i and thus total number of states required to recognize the language L3 are

20+21+22+23 = 23+1-1=15 (using 20+21+22+...+ 2n= 2n+1-1)

Remark: Let L20 be the language of strings of length 20 or more, defined over Σ = {a,b}, and the 20th letter

from the right is 1, then following the previous method, number of states for the corresponding FA is

220+1-1=2,097,151.

However, it may be noted that any portion of memory of a computer that can accommodate 21 bits can be in 221

possible states i.e. 221 possible choices for the informational content.

Distinguishable strings and Indistinguishable strings

Two strings x and y, belonging to Σ*, are said to be distinguishable w.r.t a language L ⊆ Σ* if there exists a

string z belonging to Σ* s.t. xz OE L but yz oe L or xz oe L but yz OE L .

Two strings x and y, belonging to Σ*, are said to be indistinguishable with respect to a language L ⊆ Σ* if for

every string z belonging to Σ*, either both xz or yz OE L or both don't belong to L.

Example

Let L be the language of strings, defined over Σ = {0,1}, ending in 01.

The strings 110 and 010011 are distinguishable w.r.t L, as there exists 1 belonging to Σ* s.t. 1101 belongs to L

but 0100111 doesn't belong to L.

But 111 and 010011 are indistinguishable, for 1 belonging to Σ* s.t. both 1111 and 010011 don't belong to L

i.e. for every z belonging to Σ*, either both 111z and 01001z belong to L, or both don't belong to L.

Theorem

Statement

If L is a language over an alphabet Â and for integer n there are n strings from Â*, any two of which are

distinguishable w.r.t. language L, then any FA recognizes L must have at least n states.

(Note: There may not exist any FA which recognizes the given language.)

Proof

Let S be set of strings, any two of which are distinguishable w.r.t. language L. Let F1 be the FA which

recognizes the language L. To prove the theorem, it is sufficient to show that any two strings under F1 must be

ended in different states i.e. corresponding to each string x belonging to S, F1 ends in distinct states.

Thus if S has n strings then it is to be shown that F1 has at least n states.

Theory of Automata

(CS402)

Let x and y be any two strings from S. By supposition any two strings of S are distinguishable w.r.t. L, so there

exists a string z belonging to Â*such that only one of xz and yz belongs to L i.e.F1 ends in a final state either for

xz or yz which shows that F1 ends in distinct states for xz and yz.

Let F1 be ended in same state for both the strings x and y, which shows that F1ends in same state for both xz and

yz, a contradiction as x and y being distinguishable implies xz and yz are ended at distinct states of F1.

Hence F1 does not end in a same state for both strings x and y, which shows that each pair of strings belonging

to S ends in different states. Hence F1 must contain at least n states.

Table of Contents: