 |
Decidablity, Parsing Techniques |
| << Non-Context-Free language, Pumping lemma for CFLs |
| Turing machine >> |

Theory of
Automata
(CS402)
Theory of
Automata
Lecture
N0. 44
Reading
Material
Introduction
to Computer Theory
Chapter
18
Summary
Decidability,
whether a CFG generates certain string
(emptiness), examples, whether a
nonterminal is used in
the
derivation of some word
(uselessness), examples, whether a CFL is
finite (finiteness), example, whether
the
given
string is generated by the given
CFG (membership), example, parsing
techniques, top down
parsing,
example
Decidablity
Following
are the decidable problems w.r.t.
CFG
Whether or
not the given CFG
generates any word? Problem of
emptiness of CFL.
Whether or
not the given CFG
generates the finite
language? Problem of finiteness.
Whether or
not the given string w can
be generated by the given
CFG? Problem of membership.
Following
are algorithms showing that
the answers to the above
three questions are
yes.
Algorithm
1 (Emptiness)
If the
given CFG contains a
production of the form S∆L, then
obviously the corresponding CFL is not
empty. If
the
CFG contains the production
of the form S∆t, where t is a
terminal or string of terminal then t is
a word of
the
corresponding CFL and CFL is not
empty.
If the
CFG contains no such
production then
For
each nonterminal N with N∆t, pick
one production for N (if
there are more than one) and
replace N by t in
the
right side of each
production wherever it lies.
Remove all such productions
from the CFG. Doing so
the
CFG
will be changed, it will
generate atleast one word of
the old CFL.
Repeat
the process until either it
eliminates S or no new nonterminal is
eliminated.
If S has
been eliminated then CFG
generates some words otherwise
not.
Example
S∆AB, A
∆BSB,
B∆CC
C∆SS
A∆a|b
C ∆b|bb
Step
(1). Picking A∆a, C ∆b, it can
be written as
S∆aB
A∆BSB
A∆bb
B∆aaS
B∆bb
C∆SS
Step
(1). Picking B∆bb and
A∆bb, it
can be written as
S∆abb
A∆bbSbb
B∆aaS
C∆SS
Since
S∆abb
has been obtained so, abb is
a word in the corresponding
CFL.
To determine whether
the nonterminal X is ever
used in the derivation of
word from the given
CFG, following
algorithm
is used
Algorithm
2 (Uselessness)
Find
all unproductive nonterminals (the
nonterminal is unproductive if it cannot
produce a string of terminals).
Eliminate
all productions involving unproductive
nonterminals.
Paint
all X's blue.
139
Theory of
Automata
(CS402)
If any
nonterminal is in the left
side of the production with
any blue nonterminal in the
right side, paint
that
nonterminal
blue and paint that nonterminal blue at
all occurrences of it throughout
the grammar.
Repeat
step 4 until no new
nonterminal is painted.
If S is blue
then X is useful member of CFG, otherwise
not.
Example
Consider
the following CFG
S∆Aba
|
bAZ
|
b
A∆Xb | bZa
B∆bAA
X∆aZa|aaa
Z∆ZAbA
To determine whether X
is ever used to generate
some words, unproductive nonterminals are
determined. Z is
unproductive
nonterminal, so eliminating the productions
involving Z.
S∆Aba|b
A∆Xb
B∆bAA
X∆aaa
X is blue, so A is
blue. Thus B and S are also
blue. Since S is blue so X can be
used to generate certain
word
from
the given CFG.
Note: It
may be noted that a
nonterminal is called useless if it
cannot be used in a production of
some word.
Following
algorithm is used to determine whether
the given CFG generate
the finite language
Algorithm
3 (Finiteness)
Determine
all useless nonterminals and eliminate
all productions involving these
nonterminals.
For
each of the remaining nonterminals,
determine whether they are self-embedded (using
the following steps).
Stop if a
self-embedded nonterminal is discovered.
To test
whether X is self-embedded
Change
all X's on the left side of
the productions into a Greek letter
Ψ
and
keep all X's on the right
side as such.
Paint
all X's blue.
If Y is
any nonterminal on the left
side of the production with
X in the right side, then
paint Y blue.
Repeat
step (c) until no new
nonterminal is painted.
If Ψ is
painted, then the X is
self-embedded, otherwise not.
If any
nonterminal, left in the grammar,
after step 1, is self-embedded then
the language generated is
infinite,
otherwise
finite.
Example
Consider
the CFG
S∆ABa|bAZ|b
A∆Xb|bZa
B∆bAA
X∆aZa|bA|aaa
Z∆ZAbA
Here the
nonterminal Z is useless, while
all other are used in the
derivation of some word. So
eliminating the
productions
involving Z
S∆ABa|b
A∆Xb
B∆bAA
X∆bA|aaa
Starting
with nonterminal X. Replacing X on left
side of the production by Ψ
S∆ABa|b
A∆Xb
B∆bAA
Ψ ∆bA|aaa
X is blue so A is blue
and so Ψ is blue.
Since A is blue, so B is blue and so S is
blue. Since Ψ is blue so X
is
self-embedded
and hence the CFG
generates the infinite
language.
To determine whether a
string is generated by the given CFG,
following algorithm is
used
Algorithm
4 (The CYK algorithm)
140
Theory of
Automata
(CS402)
This
algorithm was invented by John
Cocke and later was published by Tandao
Kasami and Daniel H.
Younger.
Convert
the given CFG in
CNF.
Let
the string x under consideration has the
form x=x1x2x3...xn where
all xis may not be
different. List all
the
nonterminals in
the given CFG, say, S, N1,N2, ...
List
the nonterminals that generates single
letter substrings of x i.e.
Substring
All
producing nonterminals
x1
N...
x2
N...
∂
x3
∂
∂
xn
N...
List
the nonterminals that generates
substrings of length 2 i.e.
Substring
All
producing nonterminals
x1 x2
N...
x2 x3
N...
∂
x3 x4
∂
∂
xn-1 xn
N...
Similarly,
list of nonterminals generating substring of x of length
3
Substring
All
producing nonterminals
x1 x2 x3
N...
x2 x3 x4
N...
∂
x3 x4 x5
∂
∂
xn-2 xn-1 xn
N...
141
Theory of
Automata
(CS402)
Continuing
the process, the nonterminals
that generate x1x2x3...xn can
be determined as
Substring
All
producing nonterminals
x1 x2 x3...xn
N...
If S is
among the set of all
producing nonterminals, then x can be
generated by the CFG, otherwise
not.
Example
Consider
the following CFG in
CNF
S∆AA
A∆AA
A∆a
Let x =
aaa. To determine whether x can be
generated from the given
CFG let x = x1x2x3 where x1 = x2 = x3 = a
According
to CYK algorithm, the list
of nonterminals producing single letter double letter
substrings of x and
the
string x itself, can be determined as
follows
Substring
All
producing nonterminals
x1 = a
A
x2 = a
A
x3 = a
A
x1 x2
S,
A
x2 x3
S,
A
x = x1 x2 x3
S,
A
Since S
is in the list of producing nonterminals, so
aaa can be generated by the
given CFG.
Parsing
Techniques
Recall
the CFG for arithmetic
expression
S∆S+S|S*S|number
It was
observed that the word 3+4*5
created ambiguity by considering its
value either 23 or 35. To remove
this
ambiguity,
the CFG was modified
to
S∆(S+S)|(S*S)|number
There
arises a question that whether a
new CFG can be defined
without having parentheses
with operator
hierarchy
(i.e.
*
before +)? The answer is
yes. Following is the
required PLUS-TIMES grammar
S∆E, E∆T+E|T,
T∆F*T|F,
F∆(E)|i
Where i
stands for any identifier
i.e. number or of
storage location name (variable).
Following is the
derivation
of
i+i*i
S fiE
fiT+E
fiF+E
fii+E
fii+T
fii+F*T
fii+i*T
fii+i*F
fii+i*i
Parsing
of word
Definition
The
process of finding the
derivation of word generated by
particular grammar is called parsing.
There
are different parsing techniques,
containing the following
three
142
Theory of
Automata
(CS402)
Top
down parsing.
Bottom up
parsing.
Parsing
technique for particular grammar of
arithmetic expression.
Top
down parsing
Following
is an example showing top down parsing
technique
Example
Consider
PLUS-TIMES grammar and a word
i+i*i.
As can be
observed from the name of top
down parsing, the parsing
starts from the nonterminal
S and the
structure
similar to that of total language
tree is developed. The branches of
the tree are extended
till the
required
word is found as a
branch.
Some
unwanted branches ( the branches
that don't lead to the
required word) are dropped.
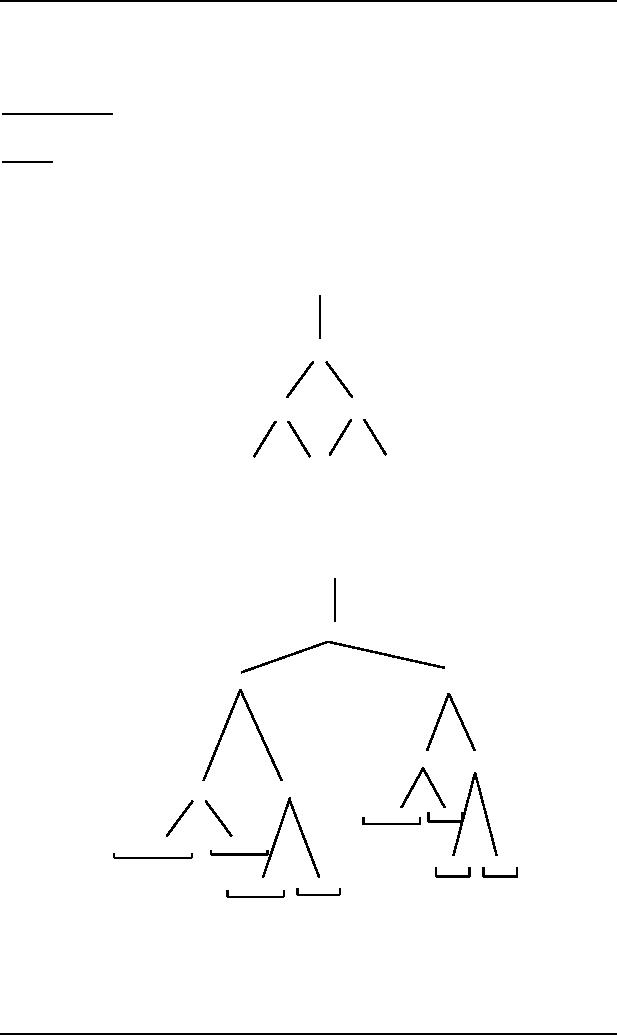
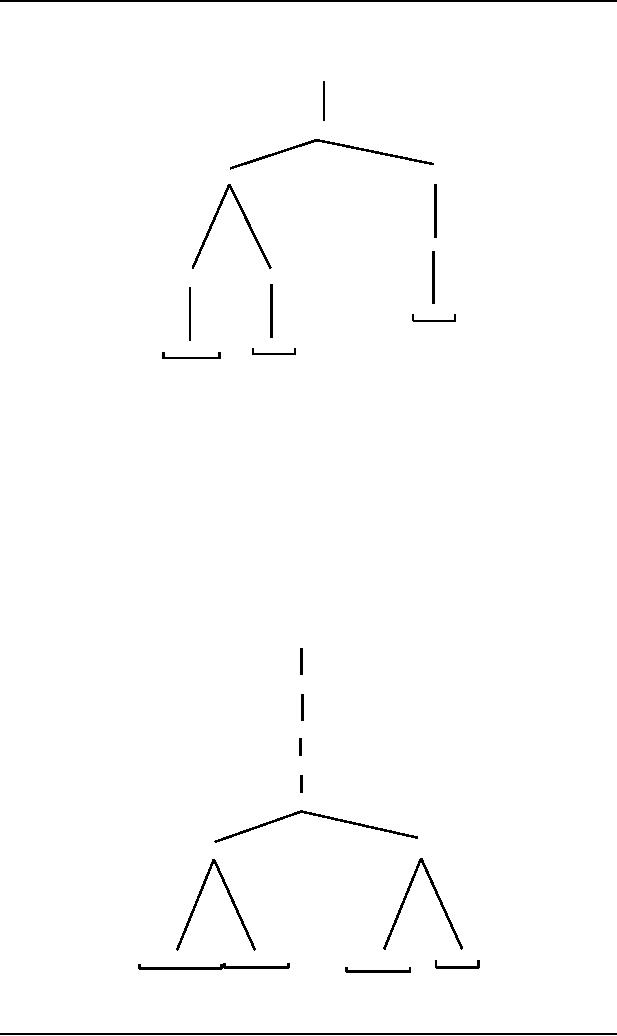
For the word i+i*i
,
the total
language tree can be started
as
S
E
Which
can further be extended
to
T
T+E
F+E
F*T
F
F*T+E
S
E
T
T+E
F*T
F
F+E
F*T+E
(E)*T
i*T
(6)
(5)
i*T+E
(E)*T+E
(2)
(E)
i
(1)
i+E
(E)+E
(7)
(8)
(4)
(3)
Dropping
the unwanted branches 1,3,5,7and
8
143
Theory of
Automata
(CS402)
S
E
T
T+E
F*T
F+E
F*T+E
i*T
(6)
i+E
i*T+E
(4)
(2)
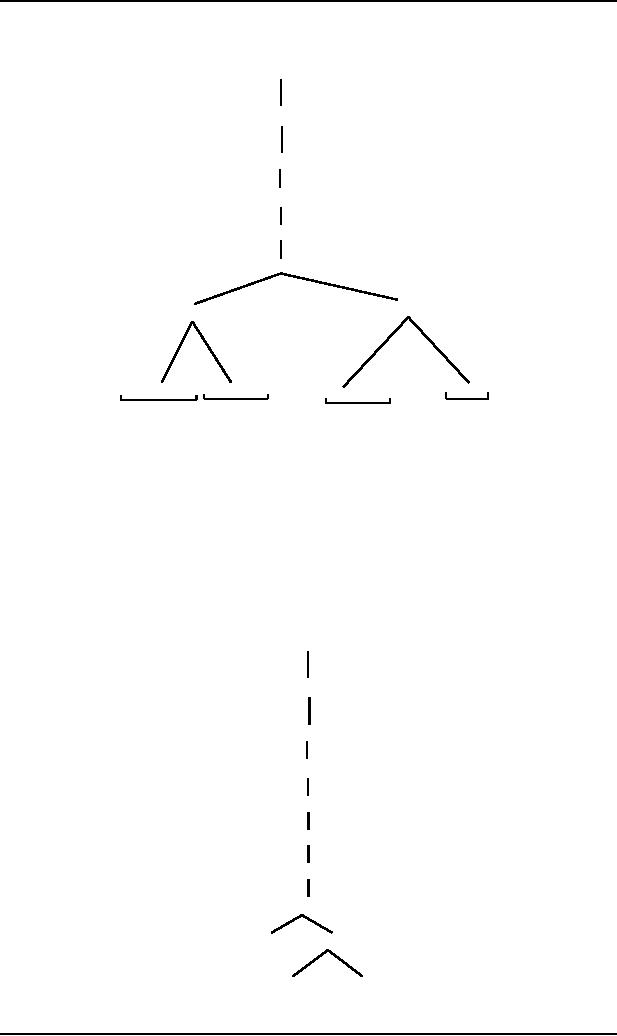
Since
first two letters in
branches 2 and 6 are not
that in i+i*i , so 2 and 6
can be dropped and using left
most
derivation
the nonterminal T is replaced
as
S
E
T+E
F+E
i+E
i+T
i+T+E
i+F+E
i+F
i+F*T+E
i+F*T
(12)
(10)
(9)
(11)
144
Theory of
Automata
(CS402)
since
(9) gives more than five
letters and (10) contains
two + so (9) and (10)
are dropped and left
most
nonterminal
F is replaced as
S
E
T+E
F+E
i+E
i+T
i+F
i+F*T
i+i*T
i+i
i+(E)*T
i+(E)
(16)
(14)
(13)
(15)
(13),
(15) and (16) are
again unwanted, so it can be written
as
S
E
T+E
F+E
i+E
i+T
i+F*T
i+i*T
i+i*F
i+i*F*T
i+i*(E)
i+i*i
The
above tree confirms the
required derivation
145

Theory of
Automata
(CS402)
S fiE
fiT+E
fiF+E
fii+E
fii+T
fii+F*T
fii+i*T
fii+i*F
fii+i*i
Note
It can be
noted that Bottom Up Parsing
can be determined similar to that of
Top Down Parsing with
the change
that in
this case, the process is
started with the given
string and the tree is
extended till S is
obtained.
146
Table of Contents:
- What does automata mean, Introduction to languages
- Kleene Star Closure, Recursive definition of languages
- Regular Expression, Recursive definition of Regular Expression
- Equivalent Regular Expressions
- Finite Automaton
- Equivalent FAs
- FA corresponding to finite languages
- Examples of TGs: accepting all strings
- Generalized Transition Graphs
- Nondeterminism, Kleeneís Theorem
- Proof(Kleeneís Theorem Part II)
- Kleeneís Theorem Part III
- Concatenation of FAs
- Closure of an FA
- Nondeterministic Finite Automaton, Converting an FA to an equivalent NFA
- NFA with Null String
- NFA and Kleeneís Theorem
- NFA corresponding to Concatenation of FAs
- Distinguishable strings and Indistinguishable strings
- Finite Automaton with output, Moore machine
- Mealy machine
- Equivalent machines
- Mealy machines in terms of sequential circuit
- Regular languages, Complement of a language
- Nonregular languages
- Pumping Lemma
- Pumping Lemma version II
- Pseudo theorem
- Decidability
- finiteness of a language
- Context Free Grammar (CFG), CFG terminologies
- Trees
- Polish Notation (o-o-o)
- Total language tree, Regular Grammar
- Null Production
- Chomsky Normal Form (CNF)
- A new format for FAs
- Nondeterministic PDA
- PDA corresponding to CFG
- Conversion form of PDA
- Conversion Form, Joints of the machine
- Row language, Nonterminals
- Non-Context-Free language, Pumping lemma for CFLs
- Decidablity, Parsing Techniques
- Turing machine