 |
Conversion Form, Joints of the machine |
| << Conversion form of PDA |
| Row language, Nonterminals >> |
Theory of
Automata
(CS402)
Theory of
Automata
Lecture
N0. 41
Reading
Material
Introduction
to Computer Theory
Chapter
15
Summary
Recap of
PDA in conversion form,
example of PDA in conversion
form, joints of the machine,
new pictorial
representation
of PDA in conversion form,
summary table, row sequence,
row language.
Conversion
form of PDA
Definition
A PDA is
in conversion form if it fulfills
the following conditions:
There is
only one ACCEPT
state.
There
are no REJECT states.
Every
READ or HERE is followed immediately by a
POP i.e.
every
edge leading out of any READ
or HERE
state
goes directly into a POP
state.
No two
POPs exist in a row on the
same path without a READ or
HERE between them whether or not
there are
any
intervening PUSH states (i.e.
the
POP states must be separated
by READs or HEREs).
All
branching, deterministic or nondeterministic occurs at
READ or HERE states, none at
POP states and
every
edge
has only one label.
Even
before we get to START, a
"bottom of STACK" symbol $ is
placed on the STACK. If this
symbol is ever
popped in
the processing it must be
replaced immediately. The STACK is
never popped beneath this
symbol.
Right
before entering ACCEPT this symbol is
popped out and left.
The
PDA must begin with the
sequence
$
START
POP
HERE
PUSH
$
The
entire input string must be read
before the machine can
accept the word.
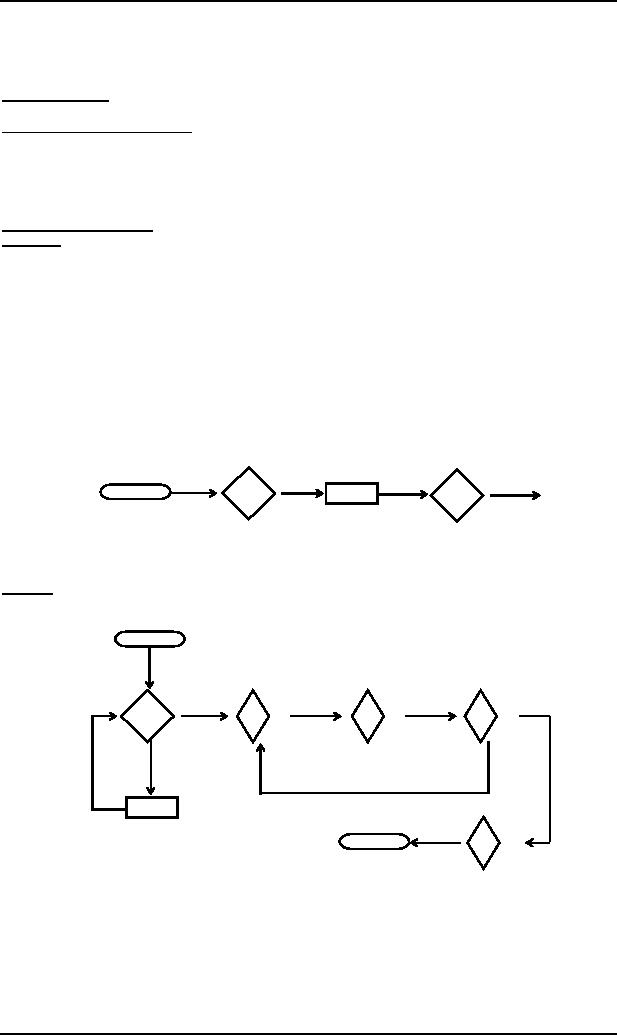
Example
Consider
the following PDA accepting
the language {a2nbn : n =
1,2,3, ...}
START
D
b
a
a
READ1
POP2
READ2
POP1
b
a
PUSH
a
$
POP3
ACCEPT
Which
may be converted to
126
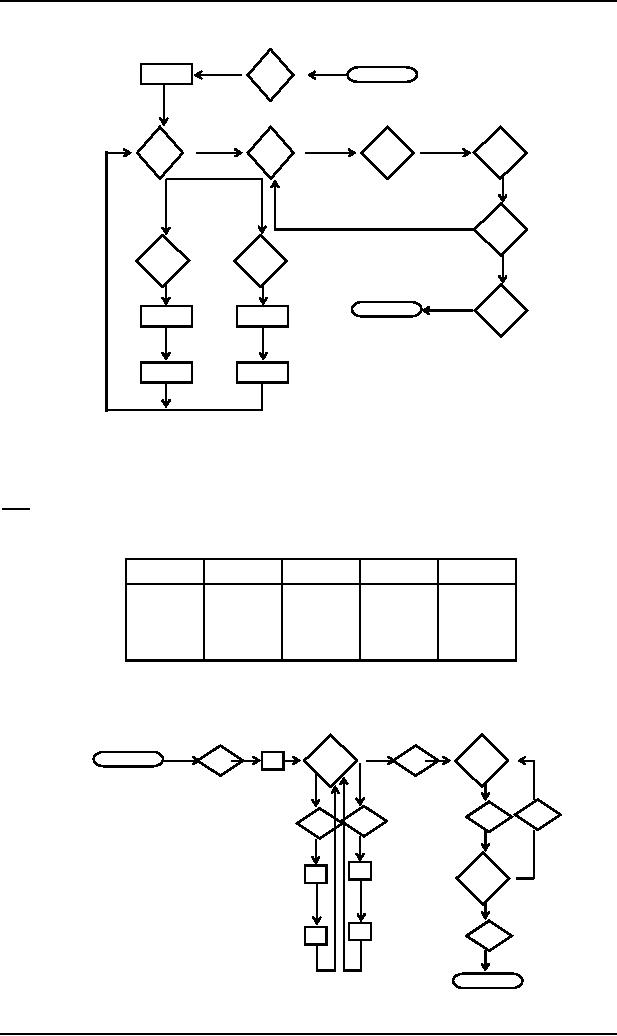
Theory of
Automata
(CS402)
$
POP4
START
PUSH
$
a
b
READ1
POP2
POP1
HERE
a
a
a
b
READ2
POP5
POP6
D
a
$
$
POP3
ACCEPT
PUSH
a
PUSH
$
PUSH
a
PUSH
a
The
above PDA accepts exactly
the same language
Note
It may be
noted that any PDA
which is in conversion
form can be
considered to be the collection of
path
segments,
where each path segment is of
the following form
FROM
TO
READ
POP
PUSH
START
READ
ONE
or
Exactly
Any
or
READ
or
HERE
no
input
one
string
or
STACK
onto
the
or
HERE
letter
ACCEPT
character
STACK
START,
READ, HERE and ACCEPT
states are called the joints of
the machine. Between
two consecutive
joints on a
path exactly one character
is popped and any number of characters
can be pushed.
The
PDA which is in the conversion
form can be
supposed to be the set of joints
with path segments in
between,
similar to a TG
START
READ1
HERE
READ2
ACCEPT
127
Theory of
Automata
(CS402)
The
above entire machine can be
described as a list of all
joint-to-joint path segments, called
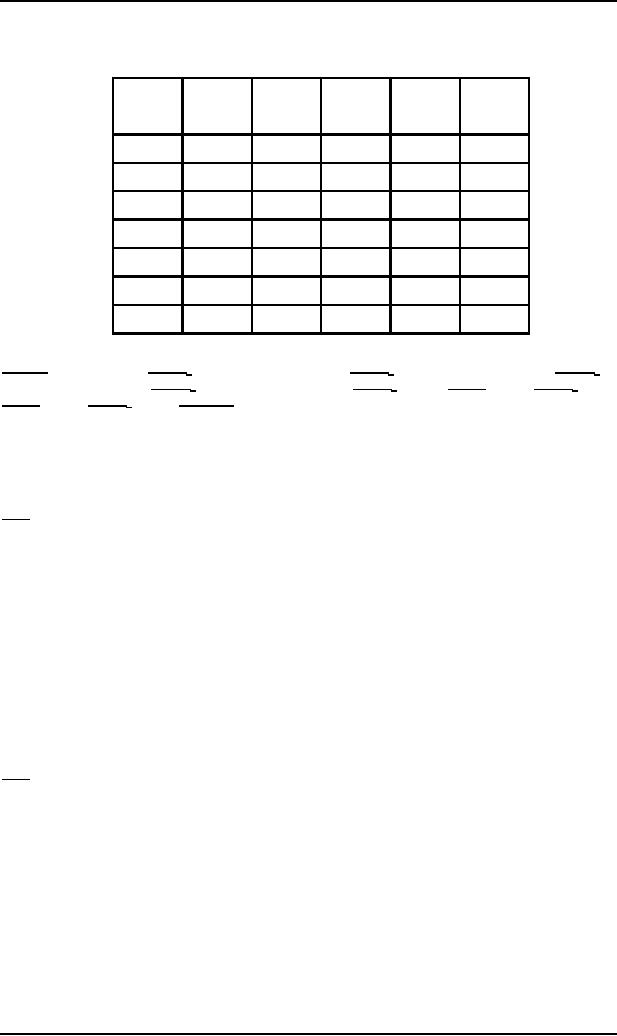
summary table.
The
PDA converted to the conversion
form has
the following summary
table
FROM
TO
READ
POP
PUSH
ROW
Where
Where
What
What
What
Number
L
START
READ1
$
$
1
READ1
READ1
a
$
a$
2
READ1
READ1
a
a
aa
3
READ1
HERE
b
a
--
4
L
HERE
READ2
a
--
5
READ2
HERE
b
a
--
6
D
READ2
AT
$
--
7
Consider
the word aaaabb. This
word is accepted by the
above PDA through the
following path
START-POP4-PUSH$-READ1-POP6-PUSH $-PUSH a-READ1-POP5-PUSH a-PUSH
a-
READ1-
POP5-PUSH a-PUSH a-READ1-POP5-PUSH a-PUSH a-READ1-POP1- HERE-POP2-READ2-POP1-
HERE-POP2-READ2-POP3-ACCEPT.
The
above path can also be
expressed by the following
path in terms of sequence of
rows
Row1 Row2 Row3 Row3 Row3 Row4 Row5 Row6 Row5 Row7
It can be
observed that the above path
is not only joint-to-joint
consistent but STACK
consistent as
well.
It may be
noted that in FAs, paths
correspond to strings of letters,
while in PDAs, paths
correspond to strings of
rows
from the summary
table.
Note
It may be
noted that since the
HERE state reads nothing
from the TAPE, therefore L is kept
in the READ
what
column.
It may
also be noted that the
summary table contains all
the information of the PDA
which is in the
pictorial
representation.
Every path through the
PDA is a sequence of rows of
the summary table. However,
not every
sequence
of rows from the summary
table represents a viable
path, i.e. every
sequence of rows may not
be
STACK
consistent.
It is
very important to determine which
sequences of rows do correspond to
possible paths through the
PDA,
because
the paths are directly
related to the language
accepted, e.g.
Row4 cannot be immediately followed
by
Row6 because Row4 leaves in HERE, while
Row6 begins in
Read2. Some
information must be kept
about the
STACK
before rows are
concatenated.
To
represent a path, a sequence of
rows must be joint-consistent
(the rows
meet up end to end) and STACK-
consistent
(when a
row pops a character it should be
there at the top of the
STACK).
The
next target is to define row
language whose
alphabet is  =
{Row1, Row2, ..., Row7} i.e.
the
alphabet
consists
of the letters which are
the names of the rows in
the summary table.
Note
It may be
noted that the words of
the row language trace
joint-to-joint
and
STACK
consistent paths,
which
shows
that all the words of
this language begin with
Row1 and end in
Row7. Consider the
following row
sequence
Row5 Row5 Row3
Row6
This is
string of 4 letters, but not word of the
row language because
It does
not represent a path starting from
START and ending in ACCEPT
state.
It is not
joint consistent.
It is not
STACK consistent.
Before
the CFG that generates
the language accepted by the
given PDA, is determined, the
CFG that generates
the
row
language is to be determined.
For this purpose new
nonterminals are to be introduced that contain
the
information
needed to ensure joint
and
STACK
consistency.
It is not
needed to maintain any information
about what characters are
read from the
TAPE.
128
Table of Contents:
- What does automata mean, Introduction to languages
- Kleene Star Closure, Recursive definition of languages
- Regular Expression, Recursive definition of Regular Expression
- Equivalent Regular Expressions
- Finite Automaton
- Equivalent FAs
- FA corresponding to finite languages
- Examples of TGs: accepting all strings
- Generalized Transition Graphs
- Nondeterminism, Kleene’s Theorem
- Proof(Kleene’s Theorem Part II)
- Kleene’s Theorem Part III
- Concatenation of FAs
- Closure of an FA
- Nondeterministic Finite Automaton, Converting an FA to an equivalent NFA
- NFA with Null String
- NFA and Kleene’s Theorem
- NFA corresponding to Concatenation of FAs
- Distinguishable strings and Indistinguishable strings
- Finite Automaton with output, Moore machine
- Mealy machine
- Equivalent machines
- Mealy machines in terms of sequential circuit
- Regular languages, Complement of a language
- Nonregular languages
- Pumping Lemma
- Pumping Lemma version II
- Pseudo theorem
- Decidability
- finiteness of a language
- Context Free Grammar (CFG), CFG terminologies
- Trees
- Polish Notation (o-o-o)
- Total language tree, Regular Grammar
- Null Production
- Chomsky Normal Form (CNF)
- A new format for FAs
- Nondeterministic PDA
- PDA corresponding to CFG
- Conversion form of PDA
- Conversion Form, Joints of the machine
- Row language, Nonterminals
- Non-Context-Free language, Pumping lemma for CFLs
- Decidablity, Parsing Techniques
- Turing machine