 |
BICONDITIONAL:UNION, VENN DIAGRAM FOR UNION |
| << BICONDITIONAL:TABULAR FORM, SUBSET, EQUAL SETS |
| ORDERED PAIR:BINARY RELATION, BINARY RELATION >> |
MTH001
Elementary Mathematics
LECTURE #
7
UNION:
Let A
and B be subsets of a universal
set U. The union of sets A
and B is the set of
all
elements in U that belong to A or to B or
to both, and is denoted A ∪ B.
Symbolically:
A
∪
B = {x
∈U
| x ∈A
or x ∈
B}
EMAMPLE:
Let
U = {a, b, c, d, e, f, g}
A
= {a, c, e, g},
B
= {d, e, f, g}
Then
A ∪
B = {x
∈U
| x ∈A
or x ∈
B}
={a,
c, d, e, f, g}
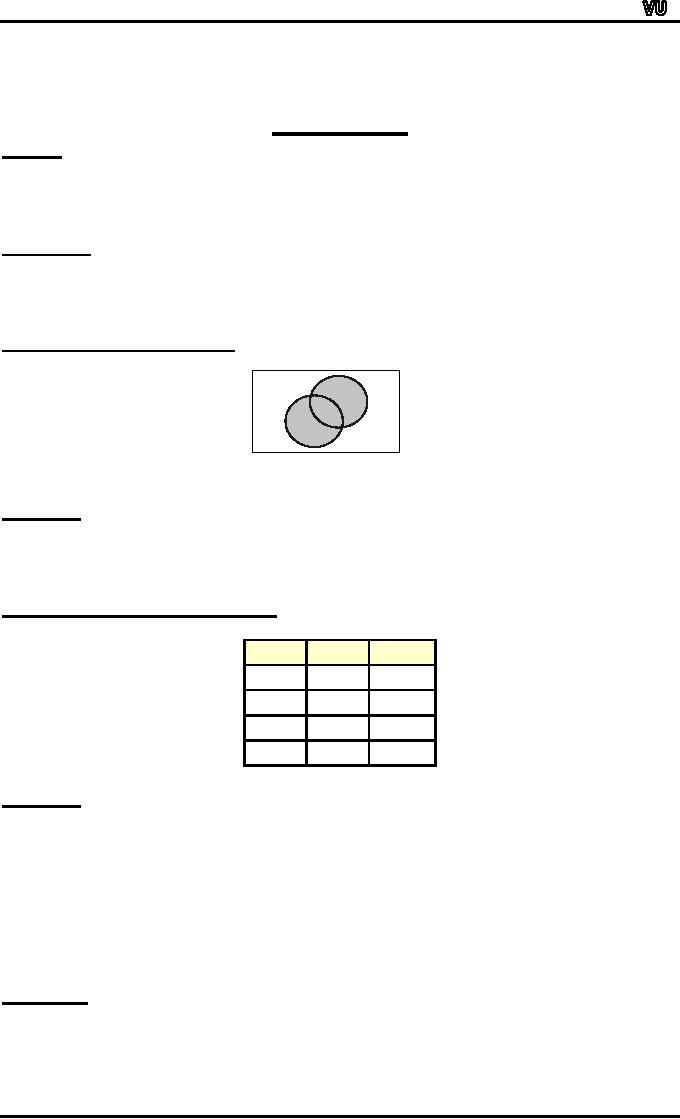
VENN
DIAGRAM FOR
UNION:
U
B
A
A
∪
B is
shaded
REMARK:
A
∪
B = B
∪
A
that is union is commutative
you can
1.
prove
this very easily only by
using definition.
A⊆A∪B
B⊆A∪B
2.
and
The
above remark of subset is
easily seen by the
definition of union.
MEMBERSHIP
TABLE FOR UNION:
A∪B
A
B
1
1
1
1
0
1
0
1
1
0
0
0
REMARK:
This
membership table is similar to
the truth table for
logical
connective,
disjunction (∨).
INTERSECTION:
Let
A and B subsets of a universal
set U. The intersection of
sets
A
and B is the set of all
elements in U that belong to
both A and B and is
denoted
A
∩
B.
Symbolically:
A
∩
B = {x
∈U
| x ∈
A
and x ∈B}
EXMAPLE:
Let
U
= {a, b, c, d, e, f, g}
A
= {a, c, e, g},
B
= {d, e, f, g}
Then
A ∩
B =
{e, g}
Page
25
MTH001
Elementary Mathematics
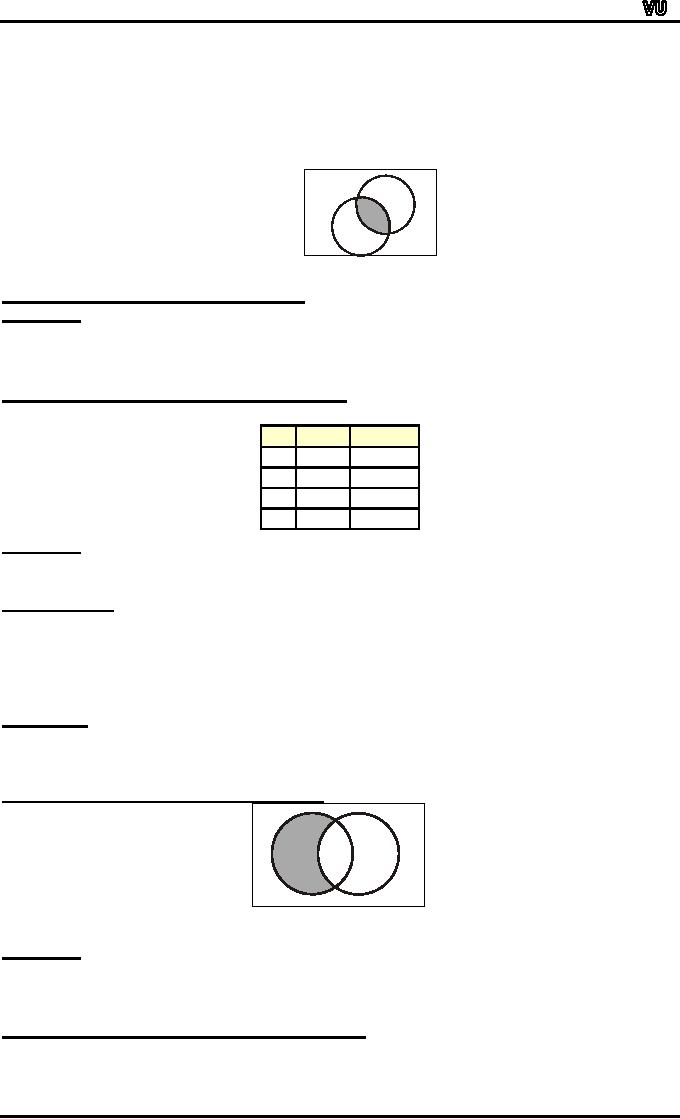
U
B
A
A
∩
B is
shaded
VENN
DIAGRAM FOR
INTERSECTION:
REMARK:
1.
A ∩
B = B
∩
A
2.
A ∩
B ⊆ A
A∩B⊆B
and
3.
If A ∩
B = φ,
then A & B are called
disjoint sets.
MEMBERSHIP
TABLE FOR
INTERSECTION:
A∩B
A
B
1
1
1
1
0
0
0
1
0
0
0
0
REMARK:
This
membership table is similar to
the truth table for
logical
connective,
conjunction (∧).
DIFFERENCE:
Let
A and B be subsets of a universal
set U. The difference of "A
and B" (or
relative
complement of B in A) is the set of
all elements in U that
belong to A but not
to
B, and is denoted A B or A \
B.
Symbolically:
A
B = {x ∈U | x ∈
A
and x ∈B}
EXAMPLE:
Let
U
= {a, b, c, d, e, f, g}
A
= {a, c, e, g},
B
= {d, e, f, g}
Then
A B = {a, c}
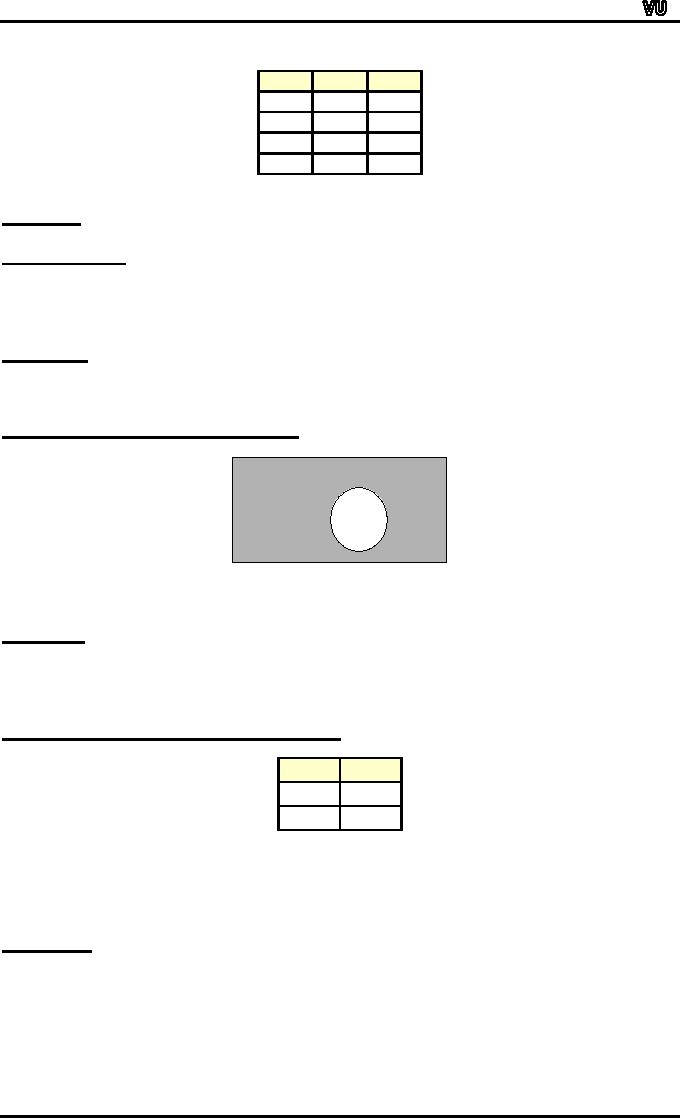
VENN
DIAGRAM FOR SET
DIFFERENCE:
U
A
B
A-B
is shaded
REMARK:
1.
A B ≠
B A
that is Set difference is
not commutative.
2.
A B ⊆
A
3.
A B, A ∩
B
and
B
A are mutually disjoint
sets.
MEMBERSHIP
TABLE FOR SET
DIFFERENCE:
Page
26
MTH001
Elementary Mathematics
A
B
AB
1
1
0
1
0
1
0
1
0
0
0
0
REMARK:
The
membership table is similar to
the truth table for ~ (p
→q).
COMPLEMENT:
Let
A be a subset of universal set U.
The complement of A is the
set of all
element
in U that do not belong to A,
and is denoted AΝ, A or Ac
Symbolically:
Ac = {x
∈U
| x ∉A}
EXAMPLE:
Let
U
= {a, b, c, d, e, f, g]
A
= {a, c, e, g}
Then
Ac =
{b, d, f}
VENN
DIAGRAM FOR
COMPLEMENT:
U
Ac
A
Ac is
shaded
REMARK
:
1.
Ac =
U A
2.
A ∩
Ac =
φ
3.
A ∪
Ac =
U
MEMBERSHIP
TABLE FOR
COMPLEMENT:
Ac
A
1
0
0
1
REMARK
This
membership table is similar to
the truth table for
logical connective
negation
(~)
EXERCISE:
Let
U
= {1, 2, 3, ..., 10},
X
= {1, 2, 3, 4, 5}
Y
= {y | y = 2 x, x ∈X}, Z = {z | z2
9 z + 14 = 0}
Enumerate:
(1)X
∩
Y
(2)
Y ∪
Z
(3)
X Z
c
c
c
(6)
(X Z) c
(4)Y
(5)
X Z
Firstly
we enumerate the given
sets.
Page
27

MTH001
Elementary Mathematics
Given
U
= {1, 2, 3, ..., 10},
X
= {1, 2, 3, 4, 5}
Y
= {y | y = 2 x, x ∈X} = {2, 4, 6,
8, 10}
Z
= {z | z2 9 z + 14 = 0} = {2, 7}
X
∩
Y =
{1, 2, 3, 4, 5} ∩
{2,
4, 6, 8, 10}
(1)
=
{2, 4}
Y
∪
Z =
{2, 4, 6, 8, 10} ∪
{2,
7}
(2)
=
{2, 4, 6, 7, 8, 10}
(3)
X
Z = {1, 2, 3, 4, 5} {2,
7}
=
{1, 3, 4, 5}
c
(4)
Y
= U Y = {1, 2, 3, ..., 10}
{2, 4, 6, 8, 10}
=
{1, 3, 5, 7, 9
c
c
(5)
X
Z = {6, 7, 8, 9, 10} {1, 3,
4, 5, 6, 8, 9, 10}
=
{7}
(6)
(X
Z)c = U (X Z)
=
{1, 2, 3, ..., 10} {1, 3, 4,
5}
=
{2, 6, 7, 8, 9, 10}
(X
Z)c ≠
Xc -
Zc
NOTE
EXERCISE:
Given
the following universal set
U and its two subsets P
and Q, where
U
= {x | x ∈
Z,0
≤
x ≤ 10}
P
= {x | x is a prime number}
Q
= {x | x2 < 70}
(i)
Draw
a Venn diagram for the
above
List
the elements in Pc ∩
Q
(ii)
SOLUTION:
First
we write the sets in Tabular
form.
U
= {x | x ∈Z, 0 ≤
x ≤ 10}
Since
it is the set of integers
that are greater then or
equal 0 and less or equal to
10.
So
we have
U=
{0, 1, 2, 3, ..., 10}
P
= {x | x is a prime number}
It
is the set of prime numbers
between 0 and 10. Remember
Prime numbers are
those
numbers which have only
two distinct
divisors.
P
= {2, 3, 5, 7}
Q
= {x | x2 < 70}
The
set Q contains the elements
between 0 and 10 which has
their square less or
equal
to 70.
Q=
{0, 1, 2, 3, 4, 5, 6, 7, 8}
Thus
we write the sets in Tabular
form.
VENN
DIAGRAM:
U
Q
2,3,5,7P
0,1,4,6,8
9,10
Pc ∩
Q =
?
(i)
Page
28
MTH001
Elementary Mathematics
Pc
= U P =
{0, 1, 2, 3, ..., 10}- {2, 3, 5,
7}
=
{0, 1, 4, 6, 8, 9, 10}
and
Pc
∩ Q = {0, 1, 4, 6,
8, 9, 10} ∩
{0,
1, 2, 3, 4, 5, 6, 7, 8}
=
{0, 1, 4, 6, 8}
EXERCISE:
Let
U
= {1, 2, 3, 4, 5},
C
= {1, 3}
and
A and B are non empty
sets. Find A in each of the
following:
A
∪
B =
U,
A∩B=φ
(i)
and
B
= {1}
A
⊂
B
and
A
∪
B =
{4, 5}
(ii)
A
∩
B =
{3},
A
∪
B =
{2, 3, 4}
B
∪
C =
{1,2,3}
(iii)
and
(iv)
A
and B are disjoint, B and C
are disjoint, and the
union of A and B is
the
set {1, 2}.
A
∪
B =
U,
A∩B=φ
(i)
and
B = {1}
SOLUTION
Since
A ∪
B = U =
{1, 2, 3, 4, 5}
and
A ∩
B = φ,
A
= Bc =
{1}c = {2, 3, 4,
5}
Therefore
A
⊂
B
and
A
∪
B =
{4, 5}
(i)
also
C
= {1, 3}
SOLUTION
When
A ⊂
B,
then
A
∪
B = B =
{4, 5}
Also
A being a proper subset of B
implies
A
= {4} or
A
= {5}
A
∩
B =
{3}, A ∪
B =
{2, 3, 4}and B ∪
C =
{1,2,3}
(iii)
Also
C = {1, 3}
SOLUTION
U
A
4
3 B
2
C1
Since
we have 3 in the intersection of A
and B as well as in C so we place
3
in
common
part shared by the three
sets in the Venn diagram.
Now since 1 is
in
the
union
of B and C it means that 1
may be in C or may be in B, but
1cannot be in B because if
be
in A ∪
B
but 1 is not there, thus we
place 1 in the part
of
1
is in the B then it
must
C
which is not shared by any
other set. Same is
the
reason
for 4 and we place it
in
the
set which is not shared by
any other set.
Now
2 will be in B, 2 cannot be in A
because
A ∩
B =
{3}, and is not in C.
So
A = {3, 4} and B = {2,
3}
A
∩
B =
φ,
B
∩
C =
φ,
A
∪
B =
{1, 2}.
(i)
Also
C = {1, 3}
Page
29
MTH001
Elementary Mathematics
SOLUTION
U
A
B
2
1
C
3
4,
5
A
= {1}
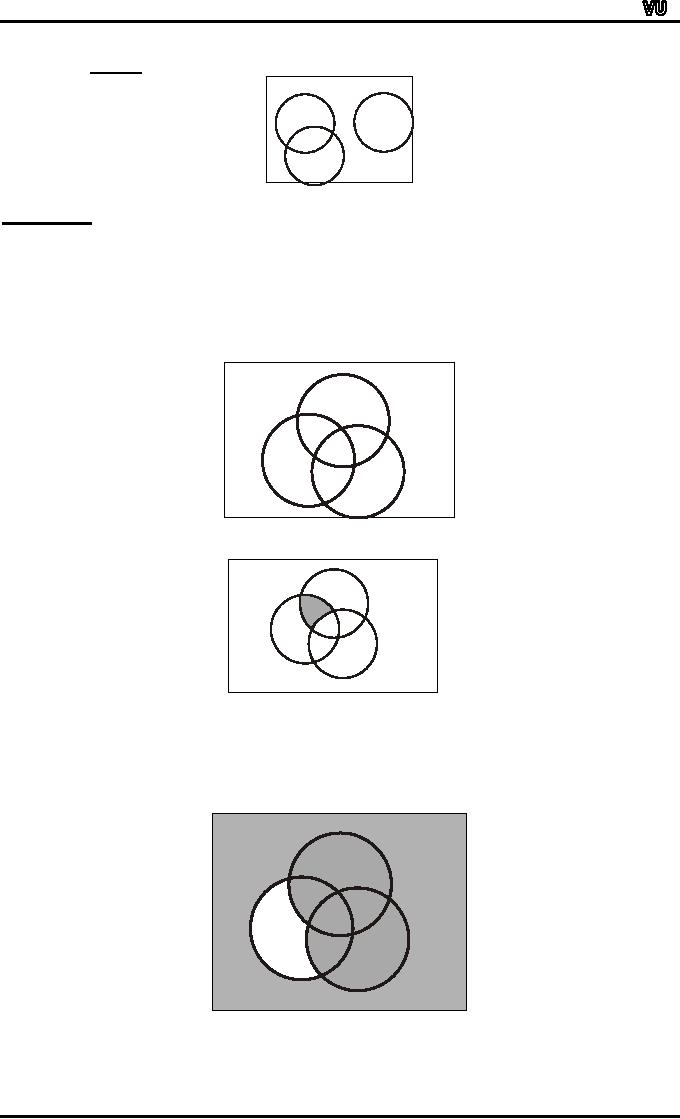
EXERCISE:
Use
a Venn diagram to represent the
following:
(A
∩
B) ∩ Cc
(i)
Ac ∪
(B ∪ C)
(ii)
(A
B) ∩
C
(iii)
(A
∩
Bc)
∪ Cc
(iv)
U
3 B
A 2
6
5
1 1
C
4
7
8
(A
∩
B)
∩
Cc
(1)
U
B
3
2
A
56
1 4
7
C
8
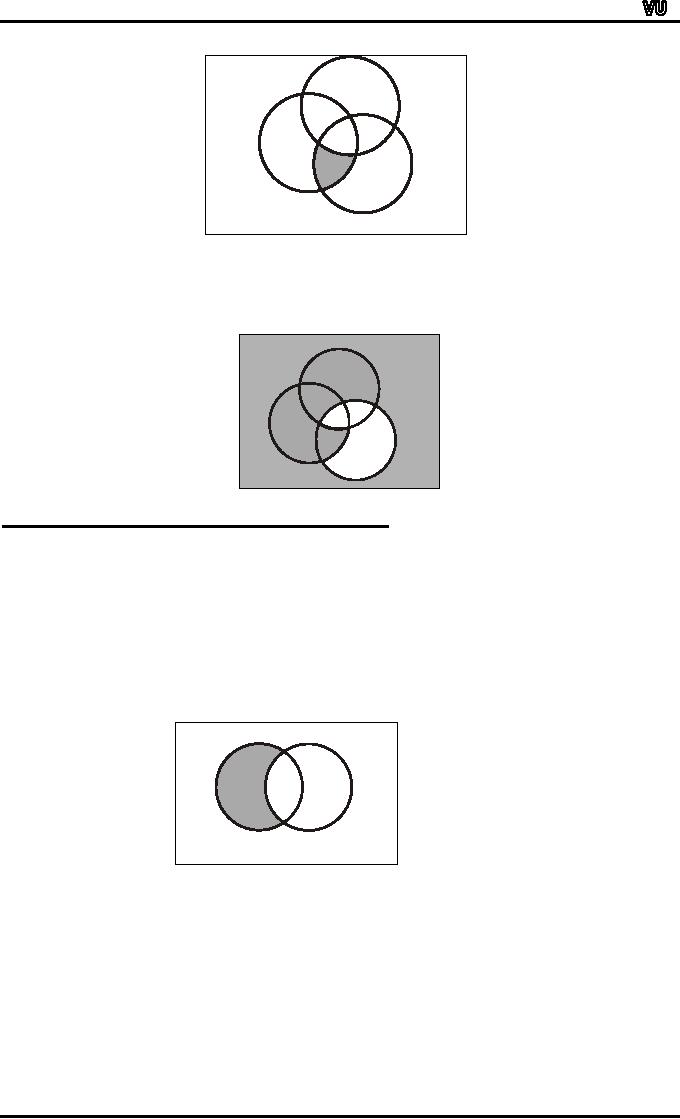
(A
∩
B)
∩
Cc is
shaded
Ac ∪
(B
∪
C) is
shaded.
(ii)
B
U
3
A
2
6
5
1
4
7 C
8
(A
B) ∩
C
(iii)
Page
30
MTH001
Elementary Mathematics
U
3
B
2
A
6
5
1
4
7
C
8
(A
B) ∩
C is
shaded
(iii)
(A
∩
Bc)
∪
Cc is
shaded.
B
U
3
2
A
6
5
C
1
4
7
8
PROVING
SET IDENTITIES BY VENN
DIAGRAMS:
Prove
the following using Venn
Diagrams:
A
(A B) = A ∩
B
(i)
(A
∩
B)c =
A c ∪
B c
(ii)
A
B = A ∩
Bc
(iii)
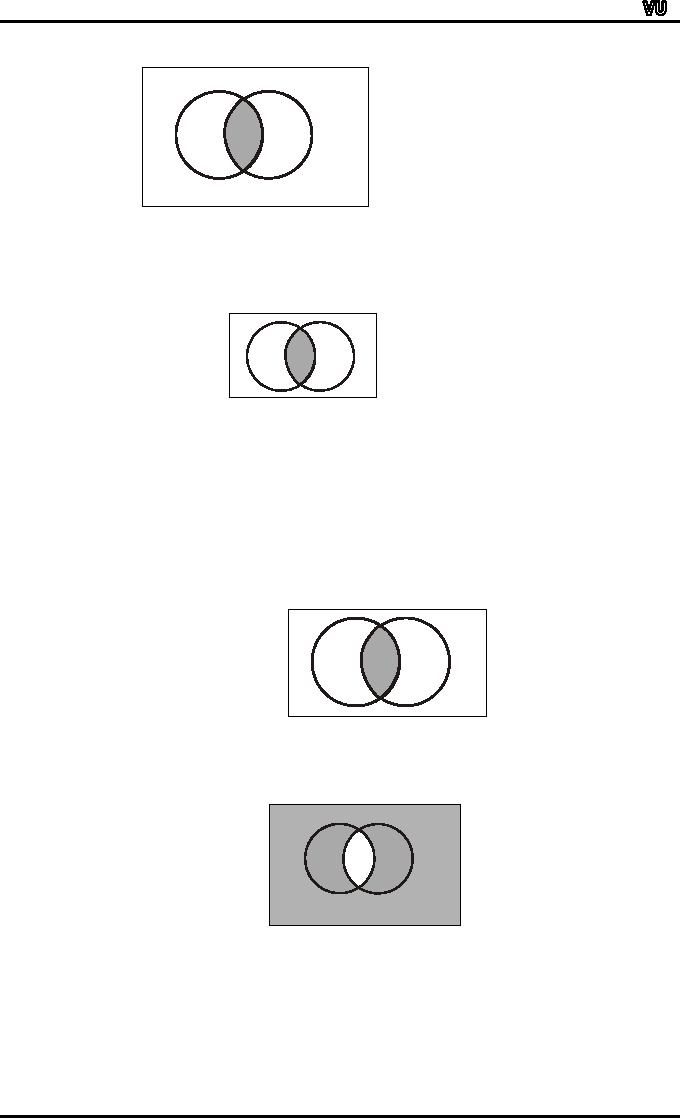
SOLUTION
(i)
A
- (A B) = A ∩
B
U
(a)
A
= { 1, 2 }
A
B
B
= { 2, 3 }
2
A
B ={ 1 }
1
3
4
A
B is shaded
Page
31
MTH001
Elementary Mathematics
(b)
U
A
B
A
= { 1, 2 }
1
AB={1}
2
3
A
(A B) = { 2 }
4
A
(A B) is shaded
(c)
U
B
A
2
3
1
4
A
∩
B is
shaded
A=
{ 1, 2 }
B
= { 2, 3 }
A
∩
B =
{2}
RESULT:
A (A B) = A ∩
B
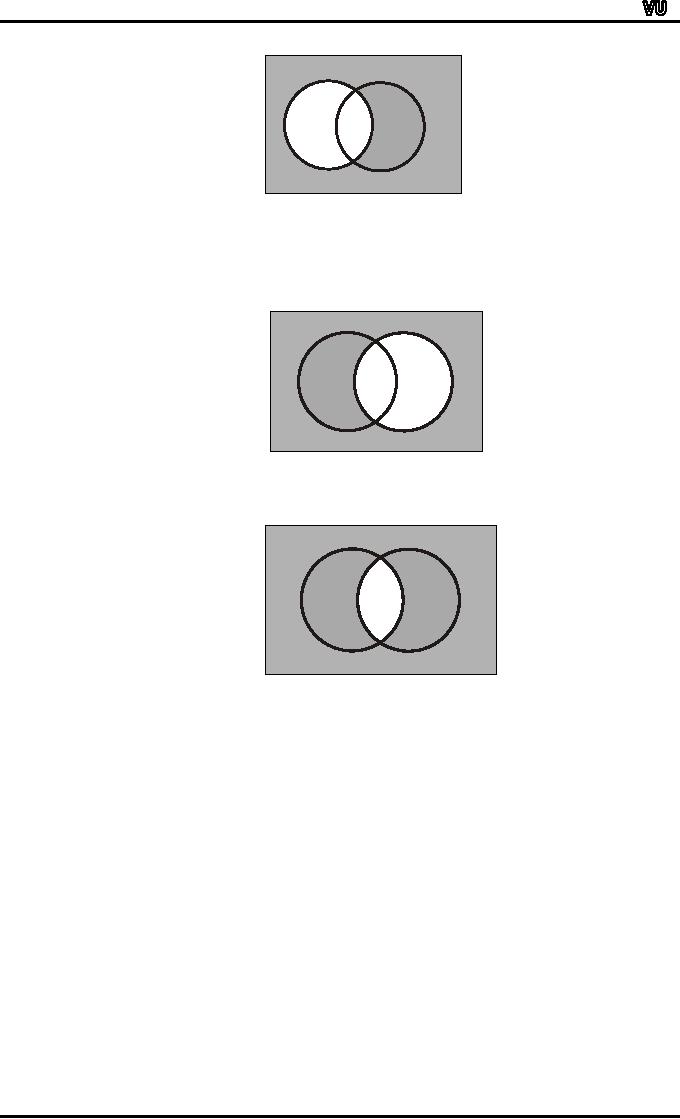
SOLUTION
(ii)
(A
∩
B)c = A
c ∪
B c
(a)
U
A
B
2
3
1
4
A∩B
U
(b)
B
A
123
4
(A
∩
B)c
Page
32
MTH001
Elementary Mathematics
(c)
U
A
B
1
A2
3
4
Ac is
shaded.
(d)
U
A
A
B
2
3
1
4
Bc is
shaded.
(e)
A
B
2
3
1
U
4
Ac ∪
Bc is shaded.
Now
diagrams (b) and (e)
are same hence
(A
∩
B)c = A
c ∪
B c
RESULT:
SOLUTION
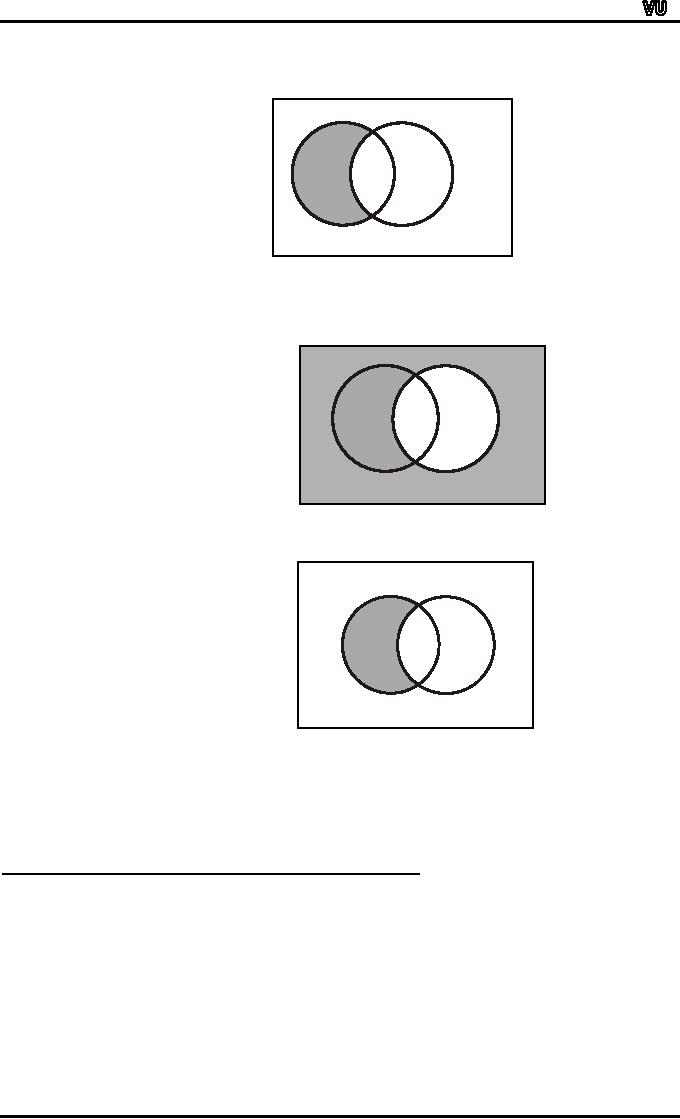
(iii)
A
B = A ∩
Bc
Page
33
MTH001
Elementary Mathematics
(a)
U
B
A
2
3
1
4
A
B is shaded.
(b)
U
A
B
1
2
3
4
Bc is
shaded.
(c)
U
A A
B
2
1
3
4
A
∩
Bc is
shaded
From
diagrams (a) and (b) we
can say
A
B = A ∩
Bc
RESULT:
PROVING
SET IDENTITIES BY MEMBERSHIP
TABLE:
Prove
the following using
Membership Table:
A
(A B) = A ∩
B
(i)
(A
∩
B)c = A c
∪
B c
(ii)
A
B = A ∩
Bc
(iii)
SOLUTION
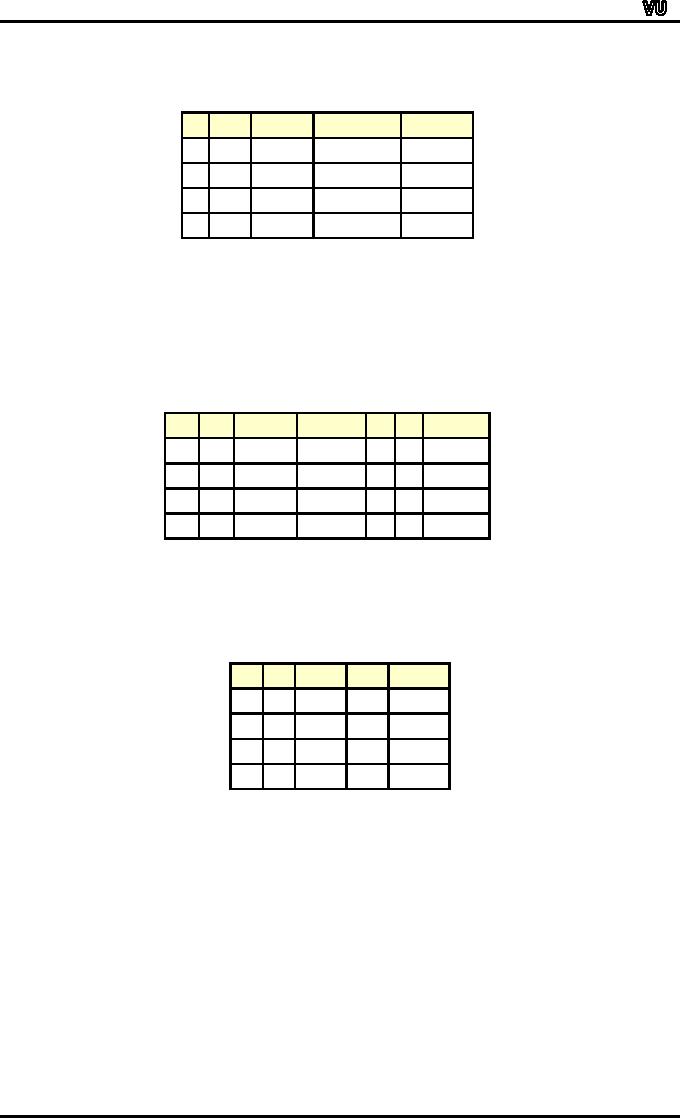
(i)
A
(A B) = A ∩
B
Page
34
MTH001
Elementary Mathematics
A∩B
A
B
A-B
A-(A-B)
1
1
0
1
1
1
0
1
0
0
0
1
0
0
0
0
0
0
0
0
Since
the last two columns of
the above table are
same hence the
corresponding
set expressions are same.
That is
A
(A B) = A ∩
B
SOLUTION
(ii)
(A
∩
B)c = A
c ∪
B c
c
c
(A∩B)c A B A
c ∪
B c
A∩B
A
B
1
1
1
0
00
0
1
0
0
1
0
1
1
0
1
0
1
1
0
1
0
0
0
1
1
1
1
Since
the fourth and last
columns of the above table
are same hence
the
corresponding
set expressions are same.
That is
(A
∩
B)c = A
c ∪
B c
SOLUTION
(iii)
Bc
A
∩
Bc
A
B
AB
1
1
0
0
0
1
0
1
1
1
0
1
0
0
0
0
0
0
1
0
Page
35
Table of Contents:
- Recommended Books:Set of Integers, SYMBOLIC REPRESENTATION
- Truth Tables for:DE MORGANíS LAWS, TAUTOLOGY
- APPLYING LAWS OF LOGIC:TRANSLATING ENGLISH SENTENCES TO SYMBOLS
- BICONDITIONAL:LOGICAL EQUIVALENCE INVOLVING BICONDITIONAL
- BICONDITIONAL:ARGUMENT, VALID AND INVALID ARGUMENT
- BICONDITIONAL:TABULAR FORM, SUBSET, EQUAL SETS
- BICONDITIONAL:UNION, VENN DIAGRAM FOR UNION
- ORDERED PAIR:BINARY RELATION, BINARY RELATION
- REFLEXIVE RELATION:SYMMETRIC RELATION, TRANSITIVE RELATION
- REFLEXIVE RELATION:IRREFLEXIVE RELATION, ANTISYMMETRIC RELATION
- RELATIONS AND FUNCTIONS:FUNCTIONS AND NONFUNCTIONS
- INJECTIVE FUNCTION or ONE-TO-ONE FUNCTION:FUNCTION NOT ONTO
- SEQUENCE:ARITHMETIC SEQUENCE, GEOMETRIC SEQUENCE:
- SERIES:SUMMATION NOTATION, COMPUTING SUMMATIONS:
- Applications of Basic Mathematics Part 1:BASIC ARITHMETIC OPERATIONS
- Applications of Basic Mathematics Part 4:PERCENTAGE CHANGE
- Applications of Basic Mathematics Part 5:DECREASE IN RATE
- Applications of Basic Mathematics:NOTATIONS, ACCUMULATED VALUE
- Matrix and its dimension Types of matrix:TYPICAL APPLICATIONS
- MATRICES:Matrix Representation, ADDITION AND SUBTRACTION OF MATRICES
- RATIO AND PROPORTION MERCHANDISING:Punch recipe, PROPORTION
- WHAT IS STATISTICS?:CHARACTERISTICS OF THE SCIENCE OF STATISTICS
- WHAT IS STATISTICS?:COMPONENT BAR CHAR, MULTIPLE BAR CHART
- WHAT IS STATISTICS?:DESIRABLE PROPERTIES OF THE MODE, THE ARITHMETIC MEAN
- Median in Case of a Frequency Distribution of a Continuous Variable
- GEOMETRIC MEAN:HARMONIC MEAN, MID-QUARTILE RANGE
- GEOMETRIC MEAN:Number of Pupils, QUARTILE DEVIATION:
- GEOMETRIC MEAN:MEAN DEVIATION FOR GROUPED DATA
- COUNTING RULES:RULE OF PERMUTATION, RULE OF COMBINATION
- Definitions of Probability:MUTUALLY EXCLUSIVE EVENTS, Venn Diagram
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:ADDITION LAW
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:INDEPENDENT EVENTS